運用柯西不等式巧解近年高校自招題

上海市行知中學(201999) 范廣哲 胡昊劼

柯西不等式是數(shù)學中最重要的不等式之一，其應(yīng)用特別廣泛，在大學數(shù)學中經(jīng)常起到非常關(guān)鍵的作用，如數(shù)學分析、線性代數(shù)、概率論、向量代數(shù)等分支中;在高中數(shù)學中同樣有著非常廣泛的應(yīng)用，如不等式證明、函數(shù)求最值、解方程組等.柯西不等式的應(yīng)用對培養(yǎng)中學生的數(shù)學抽象、數(shù)學運算、邏輯推理等數(shù)學核心素養(yǎng)有著非常重要的作用，同時也將有助于提高學生們發(fā)現(xiàn)問題、分析問題，進而解決問題的能力.

柯西不等式在高校自招數(shù)學題中也是頻頻出現(xiàn)，每次出現(xiàn)都能起到不同凡響的效果.本文列舉的高校自招題都可以用柯西不等式的方法解決，闡述柯西不等式的奇思妙用，僅供讀者參考和借鑒.部分題目來源于文獻[1]，另外部分題目來源網(wǎng)絡(luò).其中部分題目也有很多其它方法，讀者可自行思考.

首先，給出柯西不等式的表達形式，如下:

柯西(Cauchy) 不等式若a1,a2,··· ,an ∈R;b1,b2,··· ,bn ∈R，則

當且僅當bi=λai(其中λ ∈R,i=1,2,··· ,n)時等號成立.

特別地，若a1,a2,··· ,an;b1,b2,··· ,bn是兩組非零實數(shù)，取等條件即為

柯西不等式的幾個重要推論:

1.特別地，當bi=1(i=1,2,··· ,n) 時，柯西不等式為:進一步地，若ai ∈R+(i=1,2,··· ,n)，則

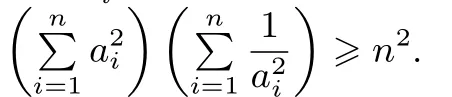
3.當ai,bi ∈R+(i=1,2,··· ,n)時，則

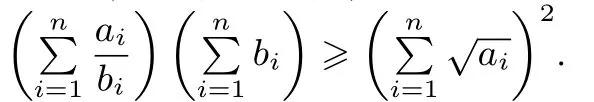
柯西不等式有很多種證明方法，本文不再贅述.柯西不等式的上述幾個推論在本文也有所體現(xiàn)，這些結(jié)論對于解題來說非常重要，能夠帶給解題人意想不到的聯(lián)想與收獲.在平時的學習過程中，要重視及時歸納總結(jié).二元與三元柯西不等式一直是高校自主招生中考查的熱點，本文列舉……