數學實驗： 學生數學思考力增長的新作用點

陳兆緒

[摘? 要] 數學思考力是指一種邏輯運用、本質聯系和信息建立的能力，也是一種搜索更廣、潛入更深的思維活動. 以數學問題為導向，以解決問題為目標，注重學生對知識的探究過程，這正是數學思考力的體現. 以數學實驗為載體，讓學生在動手操作過程中掌握思考方法，懂得思考步驟，具備思考能力，能促進學生思考力的增長.

[關鍵詞] 初中數學;數學實驗;數學思考力

德國數學家康托爾說過：“數學的本質在于思考的充分自由. ”《義務教育數學課程標準》將“雙基”調整為“四基”，即在“基礎知識、基本技能”的基礎上，增加了“基本思想、基本活動經驗”. 數學思考力是數學核心素養的核心. 數學實驗可以啟迪學生的思維. 在課堂中，以學生為中心，以實驗為手段，能使學生在數學實驗操作過程中厘清數學本質，并讓數學思考在數學教學中落地生根.

數學實驗與學習方法：讓學生

在實驗中形成主動思考意識

美國心理學家布魯納曾說：“興趣是對學習的最好刺激，一個人抱著興趣去研究某個問題時就會達到驚人的程度. ”數學實驗要求學生用觀察、思考和試驗等途徑實現知識內化，同時，實驗中一連串層層深入的問題可以激發學生的學習興趣，可以引領學生興趣盎然地走向挑戰，從而促使學生在實驗中形成主動思考的意識.

案例1?一元一次方程的應用.

演示實驗：用一個大杯向一個小杯倒水.

由于杯子的形狀不一樣，所以，在大杯往小杯倒水后，會發生水面高度的變化. 利用學生這一生活中比較常見的事例創設教學情境，能讓學生對水面高度的變化原因產生好奇，從而為后面的數學實驗做鋪墊.

教學時，為學生提供兩個底面半徑分別為3.2 cm（A）和4 cm（B）的量筒. 讓學生首先將B量筒裝滿水，其高度為4 cm，然后將量筒內的水倒進A量筒內，在此過程中認真觀察倒水前后兩個量筒內水的高度有什么變化，以及A量筒內的水面高度是多少.

在興趣的驅動下，學生開始積極地動手實驗，這種直觀的、簡單的實驗操作能讓學生很快地發現，在倒水的過程中，由于底面半徑發生了變化，所以水面的高度也隨之發生變化，但始終存在水的體積相等這一關系. 根據這一等量關系，我們可以假設A量筒內的水面高度是x cm，于是有π×42×4=π×3.22×x，解得x=6.25. 所以A量筒內的水面高度為6.25 cm.

選擇學生比較熟悉的體積問題，其等量關系一目了然. 此例能讓學生在等體積水中水面的變化過程中產生問題意識，并體會到其中所蘊含的不變量，從而引出用一元一次方程求解實際問題的基本步驟.

數學實驗與數學理解：讓學生

在實驗中思考數學概念內涵和

外延

心理認知學認為：“初中生的思維能力比較弱，且正處于想象、推理的萌芽階段. ”處于該階段的學生的思考力的形成離不開直觀形象的支撐，尤其是數學概念的理解，運用數學實驗可以幫助學生直觀地觀察數學對象，讓學生不在抽象中掙扎、徘徊，而在實驗中思考數學概念的內涵與外延，加深對數學概念的理解.

案例2?對稱軸與軸對稱圖形.

師：現在請同學們將一張紙平放在桌面上，然后往紙上滴一滴墨水，并將紙張對折壓平，稍等片刻后，打開紙，并觀察有什么現象.

學生實驗，有的學生很快發現紙張兩邊的墨跡沿著折痕折疊后重合，隨后教師出示圖1.

師：誰能說出如何剪出這幅圖案呢？請你們動手試一試.

（學生動手操作，發現將圖案對折后兩部分完全重合，所以可以利用圖形對稱的方法剪出圖案）

師：通過前面兩次操作，你們覺得它們有什么共同點？

生1：像這樣，將一個圖形沿著一條直線折疊，如果直線兩旁的部分能夠完全重合，我們就說這個圖形是軸對稱圖形，這條直線是對稱軸.

師：那我們學過的哪些圖形是軸對稱圖形？

生2：圓、等邊三角形.

生3：長方形.

生4：平行四邊形.

生5：平行四邊形好像不是軸對稱圖形.

學生中出現了不同的意見，有的贊同，有的反對，如何來驗證呢？接下來，筆者讓學生用學具進行自主操作.

生6：我從平行四邊形的一個頂點向其對邊垂直剪下一個三角形，然后將這個直角三角形拼在另一個缺口，就變成了長方形. 因為長方形是軸對稱圖形，所以平行四邊形也是.

師：聽著好像很有道理.

生7：我發現無論怎么折，兩邊都無法重合，所以我認為平行四邊形不是軸對稱圖形.

師：還有要補充的嗎？

生8：剛才我們學過，要判斷一個圖形是否為軸對稱圖形，關鍵是看它對折后兩邊是否能重合. 所以，從軸對稱圖形的概念來看，顯然平行四邊形不是軸對稱圖形.

在對稱軸與軸對稱圖形概念的教學中，筆者安排了三次數學實驗，讓學生在環環相扣的實驗中充分地思考著、體驗著、感受著，不同觀點之間相互碰撞、辯論，有效地激活了學生的思考力.

數學實驗與動態生成，讓學生

在實驗中思考“變”與“不變”

數學實驗是學生通過動手、動腦和動口“做數學”的一種學習活動，是學生綜合運用作圖工具、測量工具、模型、剪刀和紙張等工具進行數學思維的一種探究活動. 克萊因曾說過：“數學是一種精神，一種理性精神. ”其中，“理性”二字充分體現在從“變”中準確把握“不變”的本質，并能以“不變”應“萬變”.

案例3?勾股定理的探索.

問題：在△ABC中，邊AB，BC，AC的長分別為c，a，b.

（1）若△ABC為一般三角形，則a，b，c之間有什么數量關系？

（2）若∠B=∠C，則a，b，c之間有什么數量關系？

（3）若∠A=∠B=∠C，則a，b，c之間有什么數量關系？

請同學們在草稿紙上通過畫圖進行探索，從問題（1）到問題（3），從一般到特殊，讓學生認識到，當三角形的角度發生變化時，其對應三邊的關系也隨之發生變化.

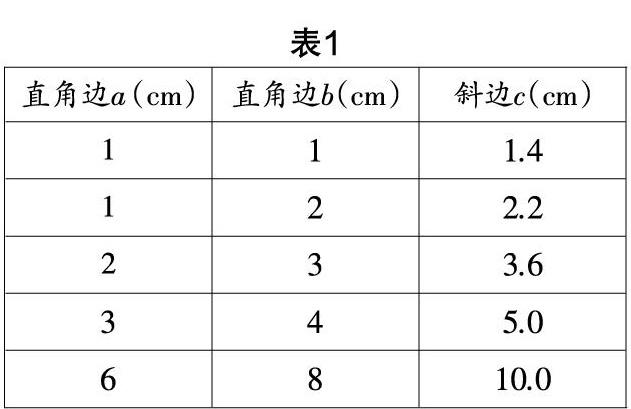
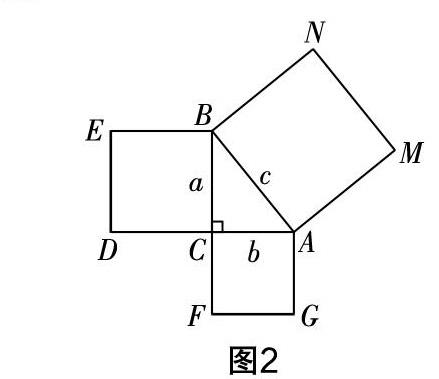
預設生成：學生從問題（1）中得到a-b

學生小組合作，借助幾何畫板制作三角形，測量各邊的長，并記錄實驗數據，展示成果.

組1：展示的成果為表1.

學生通過對數據的分析發現直角三角形的三邊滿足a2+b2=c2，這一結論是否成立，請各組學生檢查自己所做的情況，驗證是否滿足上述關系.

組2：我們發現，只有第2組的結果相差較大，其余四組均成立.

師：出現這種現象的原因是什么呢？

生1：可能a2+b2=c2并非對所有直角三角形都成立. 而且我們的實驗只有幾組數據，未必能代表全部.

生2：可能是數據取的精度不夠，如果多保留幾位，是不是誤差就會變得很小？

這是筆者在課前沒有預設到的，所以，趁學生興趣正濃厚時，筆者讓學生利用表格、幾何畫板等工具自主設計實驗，學生通過多組數據的統計分析，發現當測定的數值保留精度越高時，幾乎所有的數值都滿足a2+b2=c2. 由此，我們可以說直角三角形的兩條直角邊的平方和等于斜邊的平方，即勾股定理.

在數學學習中，學生常常因找不到突破口而困惑，此時可以通過數學實驗來發現規律，從而打開突破口. 在上述環節中，我們從特殊值出發，得到關系式a2+b2=c2，那么該關系式是否具有普適性呢？接著，學生再次從特殊回到一般，這也是學生思考力增長的難點. 分析式子的結構，可以聯想到邊長分別為a，b和c的正方形的面積，因此，想到“構造法”，對任意的直角三角形進行構造，如圖2.

此時，只需要證明正方形DCBE和CFGA的面積之和等于正方形BAMN的面積即可. 我們常用的方法是割補法. 割補的過程對學生的思維具有極大的挑戰. 只有給予學生充足的時間，鼓勵學生積極思考，勇敢面對挑戰，才能讓他們克服思維障礙. 學生在草稿紙上做了多種嘗試.

生3：我首先對a2+b2=c2進行變形，得到（a-b）2+2ab=c2，所以構造出圖3. 然后根據割補法得到圖4，接著對正方形BAMN的面積進行計算，得到S=（a-b）2+4×■ab=c2.

利用數學實驗將整個勾股定理的探索有機串聯起來，能讓學生在邊操作邊思維的過程中實現對勾股定理的猜測、驗證和證明，最后反思和總結勾股定理的證明過程，將知識上升為經驗，促進學生思考力的再次生長.

英國迪士尼樂園的路徑是游客“走”出來的，數學思考力的形成也需要依靠師生的共同努力才能形成. 在數學實驗教學中，教師應預留充足的時間給學生，從而激活他們的思考點，延展他們的數學思考觸角，讓數學思考逐漸走向開放，形成良好的思考習慣.