關注知識綜合，聚焦方法策略

苗曉麗

[摘? 要] 反比例函數(shù)與幾何綜合題在中考中十分常見，問題的考查內(nèi)容、命制形式、解析方法具有極高的研究價值，對問題開展教學探究有利于培養(yǎng)學生的數(shù)學思維. 文章對問題背景進行探討，結(jié)合實例開展思路突破、拓展探究，提出相應的教學建議.

[關鍵詞] 反比例函數(shù);幾何綜合;圖像;模型;數(shù)形結(jié)合

問題背景

反比例函數(shù)是初中數(shù)學的重點知識，需要掌握其性質(zhì)和圖像，而中考常綜合考查反比例函數(shù)和幾何知識，以常見的動點、平移、翻折、存在性等形式命題. 其問題類型多樣、難度較大，對學生的知識理解、方法掌握和解題思想有著較高的要求. 反比例函數(shù)與幾何綜合的突破關鍵為點坐標，由點坐標可以確定反比例函數(shù)曲線，而結(jié)合幾何點則可以建立幾何圖形. 對于該類綜合題有以下兩種突破思路：一是從關鍵點或線段入手，聯(lián)系點坐標和直線線段進行互化，聯(lián)合探究反比例函數(shù)與幾何特征;二是轉(zhuǎn)化、整合函數(shù)與幾何特征，構(gòu)建相應的方程，或?qū)栴}轉(zhuǎn)化為相應的函數(shù)模型，利用對應性質(zhì)來探究突破.

問題探究

中考中常見反比例函數(shù)與幾何的綜合題，其設問形式和解析思路均具有一定的代表性，具有極高的研究價值，下面以2019年江蘇省徐州市的一道壓軸題為例開展解題探究.

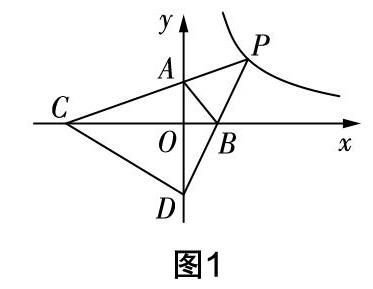
（2019年江蘇省徐州市中考卷第28題）平面直角坐標系中，O為原點，點A，B分別在y軸、x軸的正半軸上. △AOB的兩條外角平分線交于點P，P在反比例函數(shù)y=■的圖像上. PA的延長線交x軸于點C，PB的延長線交y軸于點D，連接CD.

（1）求∠P的度數(shù)及點P的坐標;

（2）求△OCD的面積;

（3）△AOB的面積是否存在最大值？若存在，求出最大面積;若不存在，請說明理由.

思路突破? 本題目主要考查反比例函數(shù)的性質(zhì)、角平分線的性質(zhì)和幾何三角形等相關知識，解題的關鍵是把握函數(shù)與幾何的關聯(lián)點——點坐標，合理構(gòu)建模型來轉(zhuǎn)化突破，對于其中的面積問題則需要充分結(jié)合面積公式，合理采用面積模型的構(gòu)建方法進行轉(zhuǎn)化解析.

解析? （1）該問求∠P的度數(shù)及坐標，需要充分利用角平分線的性質(zhì)，以及三角形內(nèi)角和定理. 已知AP和BP分別為△AOB的兩條外角平分線，則∠PAB=■∠BAY，∠PBA=■∠ABX，所以∠PAB+∠PBA=135°，則∠APB=45°. 過點P作AB的垂線，垂足為點H，再過點P分別作x軸和y軸的垂線，垂足分別為N和M，如圖2所示. 分析可證△PMA≌△PHA，△PNB≌△PHB，所以PM=PN. 根據(jù)反比例函數(shù)解析式可設點P的坐標為a，■，則a=■，可解得a=3，所以點P的坐標為（3，3）.

（2）該問求△OCD的面積，首先需要理解三角形構(gòu)建的過程，是兩條角平分線的延長線與坐標軸的交點，求三角形面積應從關鍵點或關鍵線段入手. 由于△OCD為特殊的直角三角形，則其面積可以表示為S■=■·OC·OD，顯然解題的關鍵是確定OC和OD，可以求線段長，也可以直接確定OC·OD的值.

結(jié)合條件分析可知不易直接求點C和點D的坐標，故需要求OC·OD的值，可將其視為相似三角形對應邊成比例的一部分. 連接OP，并按照圖3標識角度. 分析可知∠7+∠8=45°，又知PM∥BC，PN∥OM，則∠3=∠7，∠4=∠8，所以∠3+∠4=45°，同理可證∠1=∠4，所以△POC∽△DOP，由相似性質(zhì)可得■=■，則OP2=OC·OD，從而有OC·OD=18，所以S■=■·OC·OD=9，即△OCD的面積為9.

（3）該問探討△AOB的面積是否有最大值，三角形面積最值探究一般需要利用函數(shù)或不等式性質(zhì)，因此可以采用如下思路：整合幾何特性，結(jié)合面積公式將問題轉(zhuǎn)化為關于線段長或坐標參數(shù)的面積函數(shù)，通過函數(shù)分析來確定最值.

設BN=x，AM=y，則OA=3-y，OB=3-x，由（1）問可知AB=x+y，在Rt△AOB中使用勾股定理可得（3-x）2+（3-y）2=（x+y）2，整理可得y=■，所以S■=■（3-x）（3-y）=■. 設■=k，整理可得x2+（k-3）x+3k=0. 由于x為實數(shù)，則Δ=（k-3）2-12k≥0，可解得k≥9+6■或k≤9-6■，△AOB的面積小于9，則k≤9-6■，所以S■有最大值27-18■，即△AOB的面積存在最大值，且為27-18■.

評析? 上述反比例函數(shù)與幾何綜合題主要考查幾何面積，解析時需充分利用函數(shù)與幾何的性質(zhì). 其中第（2）問構(gòu)造了相似三角形，利用相似性質(zhì)來轉(zhuǎn)化條件;而第（3）問則利用面積模型將問題轉(zhuǎn)化為面積函數(shù)及方程，利用一元二次方程根的判別式來分析函數(shù)的最大值. 總體來看，問題突破過程中需要充分把握函數(shù)與幾何特性，借助函數(shù)及方程性質(zhì)來分析轉(zhuǎn)化.

拓展探究

上述考題主要探討反比例函數(shù)與幾何面積，屬于反比例函數(shù)背景下的面積問題，而反比例函數(shù)與幾何綜合的考查視角較多，幾何特性判斷是另一重要考查內(nèi)容，問題解析時需要充分把握幾何特性與函數(shù)性質(zhì)間的關聯(lián)，下面舉例探究.

（2018年浙江省金華市中考卷第23題）如圖4所示，四邊形ABCD的四個頂點分別在反比例函數(shù)y=■與y=■（x>0， 0

（1）當m=4，n=20時.

①若點P的縱坐標為2，求直線AB的函數(shù)表達式;

②若點P是BD的中點，試判斷四邊形ABCD的形狀，并說明理由.

（2）四邊形ABCD能否成為正方形？若能，求此時m，n之間的數(shù)量關系;若不能，試說明理由.

解析? 本題目考查反比例函數(shù)背景下幾何圖形的形狀，需從幾何特性出發(fā)來探討.

（1）①該問求直線AB的表達式，只需要提取反比例函數(shù)圖像上點A和點B的坐標即可，可求得y=■x+3.

②該問探討四邊形ABCD的形狀，需要根據(jù)點坐標來確定線段長，由線段長度關系來分析幾何形狀. 易得B（4，1），D（4，5），則點P（4，3），分析可得PA=PC=■，又知PB=PD，所以四邊形ABCD為平行四邊形;又知BD⊥AC，則四邊形ABCD為菱形.

（2）該問探究四邊形ABCD能否為正方形，根據(jù)幾何特性可知需有PA=PB=PC=PD（設為t>0）. 分析可得點B坐標為4，■，則點A坐標為4-t，■+t，所以（4-t）■+t=m，化簡得t=4-■，則點D的縱坐標值為8-■，所以點D的坐標為4，8-■.則4·8-■=n，整理可得m+n=32，即四邊形ABCD為正方形時有m+n=32.

評析? 上述綜合題以反比例函數(shù)為背景考查特殊圖形的性質(zhì)，解析時充分把握平行四邊形對角線互相平分、正方形對角線互相平分且相等的特性，而后聯(lián)合點坐標來構(gòu)建相應的代數(shù)關系，從而高效解題.

教學建議

1. 夯實基礎，方法積淀

反比例函數(shù)與幾何考題屬于綜合性問題，其中涉及函數(shù)的性質(zhì)與圖像、幾何定理定義、性質(zhì)變換等基礎知識，問題形式和知識背景變換多樣，但考查內(nèi)容均大同小異，解題的方法技巧是相通的. 開展考題探究需要從問題所涉的基礎知識、基本方法和基本思想入手，處理好通法和技巧之間的關系，合理構(gòu)建類型問題的突破思路. 例如上述問題的突破充分利用了函數(shù)與幾何的性質(zhì)，把握點坐標與幾何特性之間的聯(lián)系，以此作為突破口開展解析推導，同時融合待定系數(shù)法、交點坐標法、代數(shù)方程法等方法技巧. 因此在教學中教師需要引導學生關注問題的考查內(nèi)容，夯實基礎知識，歸納總結(jié)知識技巧，進行解題方法的積淀，從根本上提升學生的能力.

2. 延伸拓展，開放思維

把握問題內(nèi)容的主干，在此基礎上開展拓展訓練，有助于學生對問題的理解，培養(yǎng)學生思維的靈活性和廣闊性. 例如上述“拓展探究”階段中從反比例函數(shù)與幾何形狀入手開展問題探究，讓學生對該類型綜合題的考查視角有了更深刻的認識，總結(jié)了相應的突破思路. 在拓展探究過程中還體現(xiàn)了數(shù)學的拓展遷移方法，對于培養(yǎng)學生的數(shù)學思維有著一定的幫助. 因此在實際教學中，教師應引導學生開展問題拓展延伸，從問題的內(nèi)容、解法入手進行深度教學，讓學生感知問題中融合的思想方法，感悟通法解題的優(yōu)勢所在.

3. 承啟高中，數(shù)形結(jié)合

函數(shù)與幾何問題是中學數(shù)學知識融合的典型代表，該類問題具有一定的導向性，可為函數(shù)與幾何問題的突破提供解法參考. 如上述從關鍵點入手，聯(lián)系幾何特性的思路不僅適用于初中的反比例函數(shù)與幾何綜合題，對后續(xù)高中數(shù)學的同類考題也具有參考價值，因此學生在學習中需要洞悉考題結(jié)構(gòu)，總結(jié)方法思路，形成解題策略. 另外數(shù)形結(jié)合也是解析函數(shù)與幾何類考題的常用方法，數(shù)形結(jié)合解析問題，即以形助數(shù)，以數(shù)輔形，是實現(xiàn)“數(shù)”與“形”有效融合的方法. 通過數(shù)形結(jié)合可以把握曲線圖像與幾何圖形的結(jié)構(gòu)及關聯(lián)，打開問題的突破口，構(gòu)建問題解析的思路.

總之，開展考題探究應關注問題的考查內(nèi)容、解析思路和拓展方向，形成類型問題系統(tǒng)的知識與方法儲備. 反比例函數(shù)與幾何綜合題是中考的典型問題，其問題結(jié)構(gòu)和突破思路具有廣泛適用性，教師要在教學中引導學生關注問題，總結(jié)方法，強化思維，穩(wěn)步提升.