線段圖使數學思維可視化

胡偉

數學思維通常是指人們用數學的觀點去思考問題、分析問題和解決問題的認知活動過程。數學思維能力主要包括：觀察、操作、比較、猜想、嘗試、抽象、概括和推理能力等。學生在解決問題時，要經歷的思維過程有：提取有用信息，分析數量關系，尋找解題思路，最后再解決問題。這一系列的思維活動是一種心理活動過程，怎樣才能讓這種心理活動過程“可視化”？筆者認為，線段圖能夠將實際問題中所蘊涵的復雜的數學信息和抽象的數量關系形象化，用直觀的、可視化的方式表達出來，有利于探索解決問題的思路與方法，有效促進問題的解決，培養學生的數學核心素養。

線段圖幫助提取有用信息

線段圖是數學學習的重要工具。不是隨意的畫幾條線段，都能夠叫做線段圖。我們所說的線段圖應該包含以下幾個要素：數量名稱;標準統一的線段;表示出已知數量（條件）和未知數量（問題）;表示數量之間的關系。

線段圖可以幫助學生分析哪些數量是作為解決問題的條件的數量（有用信息），哪些數量是無用信息（多余條件），并將有用信息直觀地呈現在眼前。在解決實際問題的教學中，有不少題目文字敘述復雜而且抽象，可能還會存在多余條件，這就需要學生運用線段圖，從題目的大量文字中提取解決問題的有用信息，將這些數學信息直觀地呈現在線段圖上，減少了分析問題的工作記憶量，進而可以將更多的精力分配給從已知數量推導出未知數量的工作。

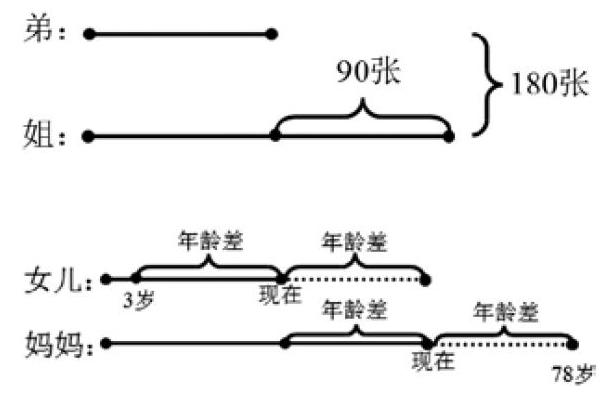
例如，媽媽的郵票張數是弟弟的3倍，妹妹比弟弟多90張，我和姐姐一共有180張郵票，姐姐和弟弟各有多少張郵票？

在這個問題中有3個信息，根據題目的問題，可以判斷“姐姐比弟弟多90張，弟弟和姐姐一共有180張郵票。”是解決這個問題的有用信息，而“媽媽郵票是弟弟的3倍”是多余條件，在解決這個問題時應舍棄。用畫線段圖應該這樣呈現（如圖），學生就很清楚地看見已知信息，隨時都能調用已知信息來分析問題，解決問題。

線段圖直觀表示數量關系

分析清楚數量關系是解決問題的關鍵所在，題目文字中呈現的數量關系往往比較抽象，要想直觀的表達數量之間的關系，線段圖是很好的工具。

線段圖使隱藏的數量關系顯性 化生活中的數學問題往往已知條件多，而且在眾多的條件之間，在條件與問題之間的聯系不明顯，需要學生通過比較復雜的記憶、理解、推理才能弄清信息與信息、信息與問題之間的數量關系，學生的思維活動最容易在這個階段受到阻礙。線段圖可以使隱藏的數量關系顯性化，從而順利分析出解答思路。

例如，“媽媽對女兒說：當我是你這么大時，你才3歲。但當你是我這么大時，我已78歲了。問：媽媽現在多少歲了？”這個問題有一定難度，它不是我們平時教學中常見的典型應用題，在這個實際問題中，可用于解決問題的條件不多，而且還都在變化。題中隱含了一些重要的信息，從字面上無法很好的表述和應用。但是如果用上線段圖，情況就不一樣了，數量關系就一目了然，3歲到78歲剛好是3個年齡差，學生很快就能通過年齡差解決問題。

利用線段圖找出數量間的對應關系 在小學高年級教學中，分數、百分數的應用對學生來說難于理解，究其原因在于學生很難找到數量間的對應關系，難以形成數量與分率的對應關系，造成無法解答或解答錯誤。但借助線段圖分析分數應用題，則可以準確地找出數量間的對應關系。

一批大米，吃了總數的40%后又買來240千克，這時的總數是原來的總數，這批大米原有多少千克？此題中，“又買來240千克”是至關重要的一個量，它是在總數剩60%后又多出來的量，畫圖時，引導學生分析題意、找準240這個量對應的分率，逐步畫出以下線段圖，就很容易列式解答了。

線段圖幫助尋找解題思路

學生經歷了用線段圖提取有用信息，用線段圖直觀表達數量關系的過程，其實是一個記憶和編碼的過程，線段圖在幫助學生對有用信息進行記憶和編碼，同時學生已在畫線段圖的過程中，對信息再進行記憶和編碼，接下來學生就能利用線段圖直觀呈現的數量信息和數量關系，尋找解決問題的思路，解決問題的思路一般有兩種：第一是分析法。從問題出發，尋找解決問題的信息，一步一步地進行探索，最后到達題目的已知條件。第二是綜合法。從數學題的已知條件出發，經過逐步的邏輯推理，最后解決所求問題。

結束語

華羅庚說過：“數缺形時少直觀，形少數時難入微。”線段圖分析問題讓學生的思維“可視化”，可以將直觀的“形”與抽象的“數”進行有機結合，體現了“數形結合”的思想方法，用線段圖分析問題能使學生在數學上獲得更好的發展。

（作者單位：四川省成都市雙流區實驗小學）