數形結合的數學教學實錄

林志勝

摘要：數形結合是一種重要的數學思想，也是一種常用的數學方法。“數”和“形”是雙邊關系，兩者通過對應和轉化，實現“以形助數，以數助形，數形互助”。通過數形結合，有利于學生分析各個數量間的關系，引發聯想，拓展思路，將復雜問題簡單化，有效提高學生的解題速度和能力。在小學數學的教學中注重運用直觀圖形，巧妙地把“數”和“形”結合起來，把抽象概念直觀化、生動化，幫助學生形成概念，有效提高課堂效率。

關鍵詞：小學數學;數形結合;實錄

數學家華羅庚曾說：“數形本相倚，焉能分作兩邊飛，數缺形時少直觀，形少數市難入微，數形結合百般好，隔裂分家萬事休。” 數形結合思想就是把數學問題中的數量關系與空間形式結合起來進行思維，從而使“數”與“形”各展其長，優勢互補，使所要解決的問題化難為易，化繁為簡。筆者結合教學實際談談數形結合思想在小學數學教學中的滲透關系。

概念算理中滲透數形結合

數學學習中離不開計算，新課標提出學生解題多樣化，但在此過程中不能忽略算理，只有理解了算理才能更好地提高數學能力。因此教師在教學中需充分利用數形結合，將抽象算理直觀呈現給學生。例如，一年級兩位數加一位數和整十數，教師通過小棒操作或小棒圖的展示，直觀形象地展示“35+3”與“35+30”的計算方法，并突出兩者在計算上的區別，使學生理解算理和算法。又如在五年級講解“異分母分數加減法”時，“畫圖法”的使用可以讓學生更直觀理解。講解的過程，教師利用數形結合讓學生體會“通分”的必要性，通過畫圖幫助學生理解，化解學習難點。

數形結合培養學生解決問題能力

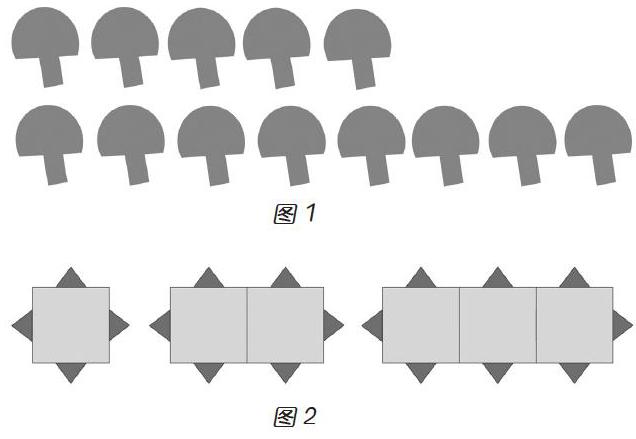
數形結合，可以直觀呈現數學問題，幫助學生將復雜的文字表達轉化為簡單的直觀圖形，培養學生解決數學問題的能力。例如，一年級上冊第15頁第四題：猜一猜，小兔子采了多少個蘑菇？作為初入小學的學生，在理解“我采的蘑菇比小白兔多，比小灰兔少”時，往往不知如何入手，這時可以采用畫圖法（如圖1）：先分別畫出小白兔和小灰兔所采的蘑菇數量，再讓學生畫出小兔子所采的蘑菇數量，答案便顯而易見了。

數形結合強化學生邏輯思維能力

兒童的認知規律一般是由感知到表象，再形成概念的過程，讓學生多角度靈活思考與想象，這對強化知識理解、提高思維能力和發展空間觀念意義重大。例如，五年級學習了“正方體與長方體的表面積”之后，學生對于幾個小正方體拼成一個長方體后面積減少多少的問題總覺得很棘手，但若借助圖形，學生很快就能明白每兩個正方體拼在一起就會減少兩個接觸面的面積這個道理，只要按題意畫出圖形，問題便迎刃而解。

數形結合提升學生發散思維

在數學教學中滲透數形結合，有利于學生分析數量之間的關系，提高解題能力和速度，發展學生的發散思維。例如，四年級下冊《植樹問題》的教學片段。

師：學校新修水泥路的一旁要栽5棵樹，請想一想，有幾種種法，并說出種植的棵數與間隔數之間的關系。（用“—”表示間隔數，用“|”表示種植的棵數）

生1：道路兩端都要栽：|—|—|—|—|

結論：種植棵數=間隔數+1

生2：只在一端栽：—|—|—|—|—|或|—|—|—|—|—

結論：種植棵數=間隔數

生3：兩端都不栽：—|—|—|—|—|—

結論：種植棵數=間隔數-1

在教師的點撥下，學生通過“畫一畫”，使種植棵數與間隔數之間的關系形象呈現，輕松發現規律，獲得了愉快的學習體驗。

又如一道拓展練習題：按這種方式（如圖2）擺桌子和椅子，一張桌子可坐4人，兩張桌子可坐6人……

問題1：按照這種方式擺桌子和椅子，10張桌子可坐（? ）人。

問題2：N張桌子可坐（? ）人。

學生通過觀察一張桌子、兩張桌子、三張桌子坐人的數量，從圖形中發現規律，進而歸納出N張桌子坐的人數，真正體現了“以形輔數”的思想，進行了思維的發散。

數形結合是一種重要的數學思想，也是一種常用的數學方法，通過數與形的對應和轉化來解決數學問題，兼有數的嚴謹與形的直觀之長，是優化解題過程的重要途徑之一。總之，教師在小學數學課堂教學中應積極滲透數形結合的思維方法，讓思維開花，為教學開辟更廣闊的天地，讓學生在數學海洋里快樂學習。

參考文獻

王文平.數形結合思想在小學數學教學中的實踐與應用[J].科學咨詢（教育科研），2020（5）.

（作者單位：廣東省汕頭市外馬路第三小學）