“一題一課”精雕細琢，反思經(jīng)驗水到渠成

陶友根 段小龍 胡健

[摘? 要] “一題一課”能通過一個題目的深入研究，完成一節(jié)課的教學任務(wù)，達成多維教學目標，讓解題教學事半功倍. 針對解析幾何的特點，在關(guān)注課堂生成的前提下，可采取相應(yīng)的“一題一課”教學設(shè)計策略，促進學生形成題后反思活動的經(jīng)驗：尋“一題多解”，形成數(shù)學語言翻譯經(jīng)驗;找表層規(guī)律，形成題目元素推廣經(jīng)驗;查前人成果，形成題目背景探源經(jīng)驗;探拓展應(yīng)用，形成知識載體推廣經(jīng)驗;究“多題一解”，形成問題模型梳理經(jīng)驗.

[關(guān)鍵詞] 一題一課;反思經(jīng)驗;教學設(shè)計

“一題一課”，就是教師通過對一道題或一個材料的深入研究，挖掘其中的學習線索與數(shù)學本質(zhì)，基于學情，科學、合理、有序地組織學生進行相關(guān)的數(shù)學探索活動，從而完成一節(jié)課的教學任務(wù)，以此達成多維目標的過程. “一題一課”的問題應(yīng)由淺入深，有層次性、開放性、廣延性，讓學生在開放的探究過程和結(jié)果中思維得到不同的發(fā)展[1].

隨著課改的推進，高考命題已經(jīng)由能力立意向核心素養(yǎng)導向轉(zhuǎn)變，怎樣提升解題教學的效率，促進學生形成解題后的反思活動經(jīng)驗，發(fā)展學生素養(yǎng)呢？“一題一課”的教學設(shè)計以一個題目為出發(fā)點，讓學生變中求進、舉一反三，定能事半功倍. 本文以2019年成都市高三二診理科數(shù)學第16題為例，基于幫助學生形成反思活動經(jīng)驗，探索解析幾何的“一題一課”教學設(shè)計策略.

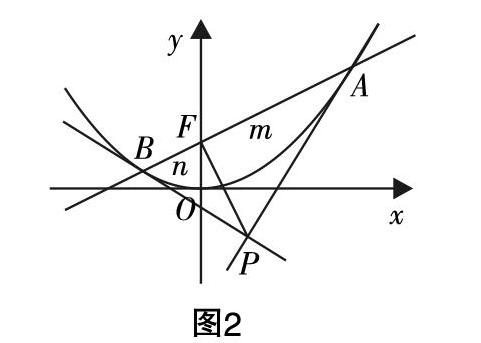
原題呈現(xiàn)：已知F為拋物線C：x2=4y的焦點，過點F的直線l與拋物線C相交于不同的兩點A，B，拋物線C在A，B兩點處的切線分別是l1，l2，且l1，l2相交于點P，則PF+■的最小值為____________. （以下簡稱“本題”）

尋“一題多解”，形成數(shù)學語言翻譯經(jīng)驗

破題的前提是理解題目，波利亞認為理解題目分為“熟悉題目”和“深入理解題目”，就是將試題的表述符號化，即翻譯題目，直譯或意譯. 直譯就是直接將文字語言翻譯為符號語言，意譯是深度翻譯，可能需要從多角度、多形式去翻譯，比如數(shù)的方面和形的方面，數(shù)或形內(nèi)部不同切入點等. 通過探尋“一題多解”，并比較其優(yōu)劣，進而總結(jié)如何優(yōu)化數(shù)學語言翻譯方式，以便得到更理想的解法. 在這個過程中，通過多角度的翻譯切入，提升學生解題活動的經(jīng)驗，尤其是數(shù)學語言翻譯經(jīng)驗.

本題分析1：直線l過點F可設(shè)為y=kx+1;直線l與拋物線C相交于不同的兩點A，B，可用直線l與拋物線方程聯(lián)立，A，B點坐標設(shè)而不求;在A，B點處的切線斜率可用求導獲得，從而寫出切線方程，求出切線交點P的坐標;得到PF，AB的關(guān)系，轉(zhuǎn)化為函數(shù)最值問題處理.具體解析如下：

由題可設(shè)l：y=kx+1，A（x1，y1），B（x2，y2），聯(lián)立直線l與拋物線的方程x2=4y，y=kx+1，可得x2-4kx-4=0.

由韋達定理有x1+x2=4k，x1x2=-4，所以AB=■x1-x2=■·■=4（k2+1）.

拋物線C：x2=4y，即y=■x2，所以y′=■x，所以切線l1，l2的方程分別為y=■x-■，y=■x-■.

聯(lián)立以上兩個方程，解得點P■，■，即P（2k，-1）.

所以PF=■=2■=■，PF+■=PF+■.

設(shè)f（x）=x+■，f ′（x）=1-■，當x=4時， f（x）有最小值6.

所以當PF=4時，PF+■的最小值為6.

本題分析2：直線l過點F，還可用直線的參數(shù)方程，設(shè)為x=tcosα，y=1+tsinα（α為傾斜角，t為參數(shù)），用參數(shù)的幾何意義求AB.（解析過程略）

本題分析3：切線方程，也可以假設(shè)切線，與拋物線方程聯(lián)立消去y，用Δ=0解出斜率，從而求解. （解析過程略）

本題分析4：得到PF+■=PF+■以后，也可以配湊為■+■+■≥3■=6. （PF=4時等號成立）（解析過程略）

通過對試題表述的多向翻譯，使學生獲得了同一問題的多個切入點，也能比較不同處理方式在計算繁雜程度的區(qū)別，優(yōu)劣緣由的探索之間感受選擇的依據(jù)，為后續(xù)優(yōu)化算法積累經(jīng)驗.

覓表層規(guī)律，形成題目元素推廣經(jīng)驗

試題總是由多種元素構(gòu)成的，解析幾何中主要有點、線、曲線等，將特殊元素改為另外的特殊元素，或?qū)⒃匾话慊浅Ｒ姷念}目變式方式，這有利于尋找相同載體下的淺層規(guī)律，同時因為這種變式通常對解法的影響較小，也能進一步強化通性通法的鞏固. 通過元素推廣研究，先猜后證，或成功或失敗，讓學生感受推廣的一般方法，形成基本活動經(jīng)驗.

本題中，如果將定點F（0，1）一般化，變?yōu)镸（0，m）（m>0），則直線l與拋物線的方程聯(lián)立x2=4y，y=kx+m，可得x2-4kx-4m=0，所以切線的交點P■，■，即P（2k，-m）. 我們發(fā)現(xiàn)，點P的縱坐標與點M的縱坐標互為相反數(shù)，同時也說明不管k如何變化，點P的軌跡是直線y=-m.

如果將定點M（0，m）再一般化，變?yōu)閽佄锞€內(nèi)的一點S（s，m），則直線l與拋物線的方程聯(lián)立x2=4y，y=k（x-s）+m，可得x2-4kx+4ks-4m=0，所以切線的交點P■，■，即P（2k，ks-m）. 消去參數(shù)k，得點P的軌跡方程為y=■x-m.

如果我們把拋物線一般化為x2=2py（p>0），拋物線內(nèi)的一定點S（s，m），則直線l與拋物線的方程聯(lián)立x2=2py，y=k（x-s）+m，可得x2-2pkx+2p（ks-m）=0，所以切線的交點P■，■，即Ppk，■.消去參數(shù)k，得點P的軌跡方程為y=■x-■m.

由此，我們得到一個一般規(guī)律：過拋物線x2=2py（p>0）內(nèi)的定點S（s，m）的直線與拋物線交于兩點，拋物線在該兩點處的切線相交，且交點在定直線y=■x-■m上.

本題的元素一般化還可以繼續(xù)，在此不贅述. 這個將點和拋物線一般化的研究過程. 研究方法基本沒有改變，卻為學生自主學習和探索提供了很好的模板，也讓學生看到規(guī)律的探尋并非遙不可及，而規(guī)律指引下的后續(xù)解題將更加輕松.

查前人成果，形成題目背景探源經(jīng)驗

解析幾何作為數(shù)學重要的分支，自創(chuàng)立起就吸引了大量優(yōu)秀的人前仆后繼地參與研究，早已碩果累累. 在“課標”把“體現(xiàn)數(shù)學的文化價值”列入基本理念后，命題者更是經(jīng)常依托數(shù)學史料，以著名問題、著名定理、著名公式或著名圖形等為切入點，融知識、方法、思想、素養(yǎng)于一體，命制出一些富有人文色彩的試題.

欣賞試題，廣泛挖掘試題的深厚背景，一方面可以學習和借鑒前人的研究成果，重走研究之路可以讓學生收獲研究的經(jīng)驗，直接吸收成果可以讓學生解小題的速度更快，解大題的方向更明確;另一方面，學生能真實感受到前人研究的豐碩成果，有利于滲透數(shù)學文化，播撒數(shù)學研究的種子.

本題的背景是阿基米德三角形，阿基米德三角形的性質(zhì)列舉（性質(zhì)眾多，只摘錄一二）：拋物線x2=2py（p>0）上不同兩點A（x1，y1），B（x2，y2），以A，B兩點為切點的切線PA，PB相交于點P，稱弦AB為阿基米德△PAB的底邊[2].

定理：若直線AB過拋物線內(nèi)一定點C（xC，yC），則另一頂點P的軌跡為一條直線，方程為xCx-p（y+yC）=0. 特別地，當C在y軸上時，即直線AB過拋物線內(nèi)一定點C（0，m）（m>0），那么：（1）另一頂點P的軌跡方程為y=-m;（2）kAP·kBP=-■（定值）.

再特殊化，直線AB過拋物線的焦點F0，■，那么：（1）另一頂點P的軌跡方程為y=-■，即準線;（2）kAP·kBP=-1，即PA⊥PB;（3）PF⊥AB;（4）△PAB的面積的最小值為p2;（5）AP與x軸交于點C，BP與x軸交于點D，xC=■，xD=■.

基于阿基米德三角形的性質(zhì)PF⊥AB，于是本題可以有以下解法：

由阿基米德三角形的性質(zhì)可得PA⊥PB，PF⊥AB.

設(shè)AF=m，BF=n，則AB=m+n，由射影定理得PF2=mn.

由結(jié)論■+■=■，即■+■=■=1，所以m+n=mn，所以PF+■=■+■≥3■=6.

追溯題目背景，挖掘背景的豐富內(nèi)涵，讓學生更好地回答問題“你知道一道與它有關(guān)的題目嗎？你知道一條可能有用的定理嗎？”[3]從而迅速地找到解題方案. 通過背景的研究，解決以此為背景的多個關(guān)聯(lián)題目，從而實現(xiàn)以點帶面解決“問題串”;通過共同參與的探源活動，為學生自主活動示范，促進學生形成探源活動經(jīng)驗.

探拓展應(yīng)用，形成知識載體推廣經(jīng)驗

橢圓、雙曲線、拋物線被稱為圓錐曲線，它們與圓有著千絲萬縷的聯(lián)系，更高層面它們同屬于二次曲線，因此在一種曲線中承載的知識和方法，很可能在另外的曲線中也會有. 將題目載體（主要曲線）平行遷移，如拋物線變?yōu)闄E圓、圓變?yōu)闄E圓等，讓知識和方法得到拓展應(yīng)用，利于學生知識和方法的體系化、深度化，同時在這一過程中，形成知識載體的推廣經(jīng)驗.

本題可將載體拋物線換為橢圓，變式為：已知F為橢圓C：■+y2=1的右焦點，過點F的直線l與橢圓C相交于不同的兩點A，B，橢圓C在A，B兩點處的切線分別是l1，l2，且l1，l2相交于點P，求點P的軌跡方程.

略解如下：

設(shè)A（x1，y1），B（x2，y2），則橢圓C在A，B處的切線方程為l1：■+yy1=1，l2：■+yy2=1，兩式聯(lián)立，得x=■，即xP=■.

當直線l與y軸不垂直時，設(shè)l的方程為x=ty+1，則x1=ty1+1，x2=ty2+1，所以x2y1-x1y2=（ty2+1）y1-（ty1+1）y2=y1-y2，故xP=2，yP=■1-■xP=-t，所以點P的軌跡方程為x=2.

當直線l⊥y軸時，橢圓C在A，B兩點處的切線平行，不符合題意.

綜上，點P的軌跡方程為x=2.

載體由拋物線換成橢圓，P的軌跡仍然為直線，學生自然產(chǎn)生了疑問，是不是圓錐曲線（甚至二次曲線）都有這樣的特點？于是引發(fā)進一步探究.

究“多題一解”，形成問題模型梳理經(jīng)驗

問題千變?nèi)f化，但萬變不離其宗，將問題提煉出模型，解法固定化（相對），有利于學生充分利用轉(zhuǎn)化與化歸思想，將不熟悉的問題轉(zhuǎn)化為熟悉的問題，將多種載體、多種表述去偽存真，九九歸一實現(xiàn)“多題一解”，提升學生解決數(shù)學問題的能力，感受反思提煉帶來的巨大收獲.

本題可提煉出“雙切線切點弦”模型，從點P0（x0，y0）引二次曲線Γ：Ax2+Bxy+Cy2+Dx+Ey+F=0的兩條切線，所得切點弦（過兩個切點的直線）有如下結(jié)論：

（1）直線方程為：Axx0+B■+Cy0y+D■+E■+F=0. 以橢圓為例，已知橢圓C：■+■=1（a>b>0），經(jīng)過橢圓C內(nèi)定點M（m，n）的直線l與橢圓C交于A，B兩點，且橢圓C在A，B兩點處的切線分別為l1，l2，若l1與l2交于點P，則點P的軌跡方程為■+■=1. 證明略. 應(yīng)用于本題中，A=1，B=C=D=F=0，E=-4，設(shè)P0（x0，y0），得切點弦方程為x0x-2y-2y0=0，因切點弦過F（0，1），所以y0=-1.

（2）當點P在直線上運動時，切點弦過定點;當切點弦過定點時，點P的軌跡是一條直線（或一部分）. 此內(nèi)容深入探究，便是射影幾何中圓錐曲線的極點極線，本文不做研究.

問題模型的建立，讓學生最終擺脫了元素、載體的束縛，得到了問題的一般解決辦法，雖說探究過程中產(chǎn)生的結(jié)論不見得能直接使用，但這種開放性探究的經(jīng)驗收獲是滿滿的，后續(xù)的解題活動必能舉一反三.

綜上所述，為了幫助學生形成題后反思活動的經(jīng)驗，我們應(yīng)多開展“一題一課”教學活動，對于解析幾何的“一題一課”教學設(shè)計，可以采用以下基本模式：尋“一題多解”——找表層規(guī)律——查前人成果——探拓展應(yīng)用——究“多題一解”. 但要注意的是，不是每個題目都有這些步驟，實際操作中要關(guān)注課堂生成，不可生搬硬套. 本文著力闡述“一題一課”的設(shè)計策略，借鑒了一些網(wǎng)絡(luò)資料，對于知識本身的介紹不夠細致和深入.

變更題目是波利亞《怎樣解題》的主旋律，“解題表”的許多問句都是直接以題目變更為目的，擬訂方案中的“你能否想到一道更普遍化的題目？一道更特殊化的題目？”解題回顧中的“你能在別的什么題目中利用這個結(jié)果或這種方法嗎？”[3]等等. 由此可見，解題教學中應(yīng)用好“題目變更”，用好經(jīng)典題目，通過“一題一課”的教學模式，對試題進行“源”與“流”的研究，進行變式拓展，最關(guān)鍵是抽象出一般模型，讓模型為以后的研究服務(wù)，實現(xiàn)“多題一解”，讓試題的價值最大化，定能事半功倍. 同時，精雕細琢教學活動設(shè)計，讓學生在反思活動中充分經(jīng)歷過程，形成基本活動經(jīng)驗，從而發(fā)展數(shù)學素養(yǎng).

參考文獻：

[1]? 吳立建. “一題一課”理念下的教學實施[J]. 江蘇教育，2018（02）.

[2]? 方亞斌. 一題一課：源于世界數(shù)學名題的高考題賞析[M]. 杭州：浙江大學出版社，2017.

[3]? G·波利亞. 怎樣解題：數(shù)學思維的新方法[M]. 徐泓，馮承天譯. 上海：上海科技教育出版社，2011.