例談回避分類討論的六大策略
張魁
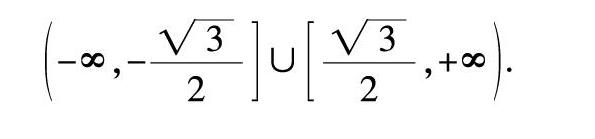

[摘? 要] 分類討論是常見而重要的一種解題策略,它較好地體現了對“能力”的考查,備受命題者的關注,是當下高考熱點問題.當然,分類討論需做到不重復、不遺漏,這就對思維的嚴謹性提出了較高的要求,學生時常會因為考慮不全面而導致解題失誤. 從優化解題過程,提高解題效率的角度來思考,有些問題可簡化或避免分類討論.文章對此進行一些歸納探究.
[關鍵詞] 高中數學;分類討論;回避;策略
正確靈活地運用數學思想,不僅可以達到化難為易的解題效果,還可以有效提升解題的大局思路與總體思考能力. 分類討論是一種行之有效的思想方法,也是一種重要的解題策略,其重要性在近幾年的高考試題中也有明顯體現.通過合理分類可以分化問題,化零為整,一一擊破難點問題,在討論時需做到不重不漏,而這在一定程度上也對學生的數學思維提出了較高的要求. 事實上,分類討論并不是所有問題都可適用,有些題型淺顯觀察似含有分類因素,但當對問題本質深入觀察和細致分析之后,又可避免繁雜的討論過程.因此,我們在關注分類討論思想應用的基礎上,也需克服動輒討論的思維定式,不可盲目而呆板地進行分類討論,而應充分挖掘潛在的特殊因素,靈活機動地運用適當的策略,從而簡化或回避分類討論.
引參換元,規避討論
換元法是將某個式子視為一個整體,引入新的變量,從而將問題轉移到對一個新對象的研究中去,使問題得到簡化. 當我們以一個新字母替換題目中的整體時,則可以規避分類討論的繁雜過程,給人以柳暗花明的感覺,從而使問題迎刃而解.
例1:當a>0時,解關于x的不等式■>a-2x.
分析:本題若先平方,則需進行分類討論從而獲解,過程煩瑣.而通過換元法令■=t,可避免討論,簡化解題過程.
解:令■=t,則t≥0,且有x=a-■. ?搖代入原不等式,據條件a>0,可化簡得2t2-at-a2<0,所以-■ ■參數分離,避繁就簡 例2:設函數f(x)=x2-1,對于任意x∈■,+∞,f■-4m2f(x)≤f(x-1)+4f(m)恒成立,試求出實數m的取值范圍. 分析:此例題若直接進行求解,需經歷多種情況的討論來解決,過程煩瑣不說,難度也較大,學生極易思維卡殼,造成錯誤.事實上,可以分離參數,解題的關鍵是將原問題完美轉化為具體函數的求最值問題,從而提高解題的速度和正確率. 解:據題意,可得■-1-4m2(x2-1)≤(x-1)2-1+4(m2-1),即■-4m2≤-■-■+1在x∈■,+∞上恒成立. 令f(x)=-■-■+1,x∈■,+∞,則當x=■時,f(x)可取到最小值,最小值為-■. 所以■-4m2≤-■,可解得m∈-∞,-■∪■,+∞. 整體思想,免于討論 所謂整體思想,望文生義就是將若干式子組合為一個整體,直接或是變形后可代入另一個式子,從而減少或回避求解單個變量而導致的煩瑣運算,使解題過程簡捷明快,而且富有創造性. 事實上,在解決一些數學問題時,若能從全局著眼深入觀察特征和本質,則可以免于討論,收到事半功倍的效果. 例3:試求出同時滿足以下兩個條件的所有復數z,①z+■∈R,且1 分析:按常規解題思路,先設z=a+bi(a,b∈R),然后再討論求解,會導致題目變得復雜,學生在計算過程中也較易出錯.這時若從整體思想入手,將z+■視為一個整體,然后化歸為一元二次方程求根,則可以有效回避討論,使復雜的題目變得簡單,從而快速、準確地得出結論. 解:設z+■=a,則有z2-az+10=0,又有1 數形結合,避免討論 數形結合是極具數學特色的信息轉化,在解題中,它呈現各種獨特優勢,如思路上的靈活,過程上的便捷,方法上的多樣等,不僅有效避免了討論,還為學生的解題提供多向通道. 例4:若直線y=x+b和曲線y=3-■有公共點,試求出b的取值范圍. 分析:對于本題,若運用一般解法將函數圖像的交點個數轉化為判斷方程解的個數,則需分類討論x的取值范圍,比較冗長,造成解題過程的混亂,此時結合圖形考慮,便可以避免這一點. 解:據y=3-■,可得(x-2)2+(y-3)2=4(y≤3),那么函數所對圖像則為一個下半圓,該半圓以(2,3)為圓心,2為半徑,且與y軸切點為A(0,3). 當直線y=x+b經過點A(0,3)時,b=3;當直線與該半圓相切時,■=2,解得b=1-2■或b=1+2■(舍去),再根據圖1進行分析,可得1-2■≤b≤3. 正難則反,另辟蹊徑 在數學解題中,一般思維是正面的、順向的,但有些數學問題從正面著手難以完成,則不妨進行逆向思考,另辟蹊徑,這就是“正難則反”策略. 在解題過程中,有一些數學問題在分類討論過程中相當麻煩,但若用補集的方法從結論的反面進行分析和探究,從而得出反面結論,再與集合性質相結合,則可以突破思維定式,使問題化難為易,讓思維進入高一階的境界. 例5:已知三條拋物線y=x2+4ax-4a+3,y=x2+(a-1)x+a2,y=x2+2ax-2a中至少有一條與x軸有交點,求a的取值范圍. 分析:本題如果從正面直接求解,則需分類討論的情形有七種之多,繁雜程度可以想象,若運用“正難則反”策略,去掉不合題意的解集,從問題的反面“3條拋物線都不與x軸相交”這一種情況著手解決,相對于命題本身更簡單、更明確,從而使問題簡化. 解:當3條拋物線都不與x軸相交時,有16a2+4(4a-3)<0,(a-1)2-4a2<0,4a2+8a<0.解得-■ 再排除掉以上3條拋物線都不與x軸相交的情況,取其補集,可得a≤-■或a≥-1. 反客為主,去除討論 所謂“反客為主”,就是當從處于“主位”的對象入手難以解決時,巧妙地更換對象,將處于“客位”的對象置于“主位”,從而形成解決問題的策略,從而避免了討論的過程,使問題得到簡化解決. 例6:對于任意m∈[-2,2],函數f(x)=mx2-mx+m-6的值總小于0,試求出x的取值范圍. 分析:本題關于x的二次函數f(x)的值總小于0,即f(x)的最大值小于0,而f(x)的最大值是由x的取值范圍來確定的. 如果單純從二次函數角度去思考,問題難度系數很大,分類情形也難以定奪. 若是能考慮到函數f(x)中的x為自變量,它占據“主位”,而m為待定常數,即置于“客位”,逆轉這兩個對象的角色,反客為主,將f(x)視為g(m)=(x2-x+1)m-6,也就是看作關于m的一次函數,則可以回避討論,解題過程由此得到優化. 解:設g(m)=(x2-x+1)m-6,則函數g(m)<0在m∈[-2,2]時恒成立. 因為g(m)為m的一次函數,所以只需g(-2)<0,g(2)<0. 即-2(x2-x+1)-6<0,2(x2-x+1)-6<0,所以x∈(-1,2). 總之,當今的數學命題,無論是能力立意,還是知識立意,都彰顯出對數學思想方法應用能力的一種考查. 在上述多個例題中可以看出,一些分類討論問題可以消除或避開引起分類討論的因素,使題目產生易解的變因素,從而簡化解題過程. 由于高考題型千變萬化,上述例題并不一定全面,還需學生在平時的訓練中多多積累,本文旨在拋磚引玉,以期引起大家的思考,在解題中挖掘數學的魅力.

