圓錐曲線中定點分弦成定比問題的探究

廣東省廣州市番禺區實驗中學(511400) 潘神龍

設點P是平面上的一定點(非原點),給定一個實數λ,圓錐曲線C是否有弦MN被點P分成的長度之比恰為λ的兩條線段? 如果有,這樣的弦有幾條? 以往人們認為此類問題解法復雜,且難以用公式表示,較少去研究它.本文系統地研究并解決了此類問題,得到以下結果:弦MN的斜率k與定比λ、μ值之間的關系,定比λ的變化規律,定點P的存在區域……并提供了處理圓錐曲線問題的一種思路.

全文假設:定點P在第一象限,直線MN與圓錐曲線C相交,|MP|≤|NP|,即?1＜λ≤1 且λ0;直線MN繞點P旋轉時沿逆時針方向.

1 圓

定理1設圓C:x2+y2=r2,定點P(x0,y0)分斜率為k的弦MN所成比為令μ=x20+y20(μ＞0,μr2),有

證明設弦MN的方程為(t為參數),將其代入圓的方程,整理得

設此方程的兩根為t1,t2,分別對應M,N兩點,根據t的幾何意義,t1=?λt2,所以λ(t1+t2)2+(λ?1)2t1t2=0;由韋達定理,

整理得(Ⅰ).

1.1 定點P 在圓內,0＜μ＜r2

(1)λ=1,弦僅有一條,與OP垂直;(2)1,弦有兩條,關于直線OP對稱;(3)弦僅有一條,過圓心;(4)?1＜且0,弦不存在.當直線MN繞點P從過圓心旋轉至與OP垂直時,λ逐漸變大.

圖1

圖2

1.2 定點P 在圓外,μ＞r2

(1)?1＜λ弦有兩條,關于直線OP對稱;(2)弦僅有一條,過圓心;(3)且λ0,弦不存在.當直線MN繞點P從過圓心旋轉至趨于與圓相切時,λ逐漸變小.

圖3

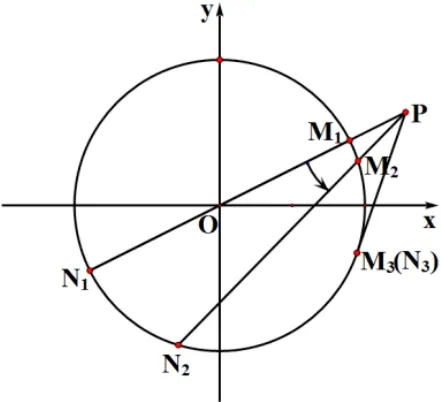
圖4

1.3 推論

推論1當時,(Ⅰ)退化為一次方程,弦有兩條,其中一條弦的斜率不存在.

推論2當弦存在時,設若λ＞0,點P滿足若λ＜0,點P滿足r2＜μ≤由此得到點P的存在區域.

推論3存在以點P為中點的弦的充要條件是0＜μ＜r2.

推論4定比λ是方程1=0 的根.

推論5弦長

證明由t1=?λt2得

2 橢圓

定理2設橢圓定點P(x0,y0)分斜率為k的弦MN所成比為令有

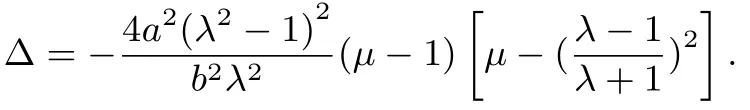
2.1 定點P 在橢圓內,0＜μ＜1.

(1)λ=1,與OP共軛的弦