一類三點共線問題的解析與探究

廣東省汕頭市潮南區礪青中學(515135) 鄭燦基

江蘇省淮安市范集中學(223215) 胡傳虎

一、問題呈現

(2019年山東棗莊市高二期末)已知圓O:x2+y2=1,點P在直線l:y=x+2 上,若圓O上存在兩點A,B,使得則點P的橫坐標的取值范圍是( )

本題以直線和圓為背景,以向量為載體,涉及三點共線問題,著重考查邏輯推理、數學運算等核心素養,需要運用數形結合、轉化與化歸等思想方法進行解題.本題看似較為平淡,實則是一道內涵豐富的好題.

二、思路分析及解答過程

本題由已知條件可以得出直線l與圓O相離,題設目標是求滿足的點P的橫坐標的范圍,需圍繞點P尋找條件,建立關于點P的關系式或不等式.本題對于不少學生而言是陌生的,P,A,B雖三點共線,但涉及的動點較多,感覺入手困難,需挖掘題目中隱含條件.

1 幾何視角

根據題目條件,數形結合,注重挖掘其中的幾何性質.

解析連結OP,設直線OP與圓O相交于C,D兩點.如圖1 所示.由得因為PD≤PB,PC≥PA,所以要使得圓O上存在兩點A,B,使得必須滿足所以(r為圓O的半徑)即PO≤2r.設P(x0,x0+2),則解得?2≤x0≤0.

2 代數視角

解析設P(x0,x0+2),A(cosα,sinα),B(cosβ,sinβ)(α≠β),可由得

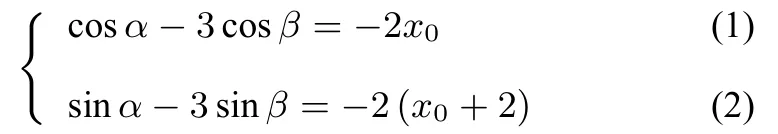
由(1)2+(2)2得10?6 cos(α?β)=4x02+4(x0+2)2.

由0≤α＜2π,0≤β＜2π知α?β ∈(?2π,0)∪(0,2π),所以?1≤cos(α?β)＜1,所以4＜10?6 cos(α?β)≤16,即4＜4x02+4(x0+2)2≤16,解得?2≤x0≤0.

點評解法1 注重挖掘圖形的幾何性質,等價轉化為是解題的關鍵,有利于培養學生的幾何直觀能力;解法2 實質上是常規解法,利用設點P的坐標建立關于橫坐標x0的關系式,利用三角函數的性質建立關于x0的不等式,進而求得x0的取值范圍,有利于培養學生的化歸和運算能力.

三、問題拓展和探究

解析幾何試題常隱藏一些幾何或代數背景,需要去深……