營造課堂氣氛，培養學生創新思維

揭志安

[摘? 要] 名師理念，起到了很好的示范、引領作用. 創新思維的發展，要從多方面、多角度進行探討、實踐. 學生核心素養的體現，課堂教學是最好的戰地，學生可以發揮得淋漓盡致. 課堂教學如何營造課堂氣氛，達到滿意的教育教學效果，提高教學質量，是教學中值得探究的問題.

[關鍵詞] 初中生;課堂氣氛;創新思維;核心素養

平常教學中，課堂上往往出現兩種不同的場面：有的教師精神飽滿，生動傳情，學生情緒高漲，注意力集中，教學雙方都沉浸在一種輕松愉快的氣氛中，積極開啟智能的機器，共同探索知識之謎;有的教師則不甚得法，講得唇干舌燥，聲音嘶啞，而學生木然處置之，毫無反應，整個課堂猶如一潭死水.

數學，注重學生思維、分析及多方面能力的培養，也就是當代教育常提的核心素養的體現. 營造活躍的課堂氣氛，培養學生創新思維發展，是每一位數學同仁值得探析的課題. 怎樣營造課堂氣氛，讓學生成為課堂的主角，培養自主學習能力，核心素養得到較好的體現？這是值得我們共同探討的問題.

■ 課堂要有疑問

書本知識源于前人總結，教師應該緊扣課本，創設問題情境，用疑問開啟學生思維的心扉. 問題，是教學活動的開端，貫穿整個教學過程的主線，是教學活動的歸宿. 營造一個學生能夠明顯意識到的疑難情境，使學生產生認識上的困惑，從而激發學生的探究，是教學成功的基本條件之一.

如教學“三角形全等”，老師準備以下教具，舉實例，并提問：一塊玻璃，不小心被打成兩塊，分為①和②，現在要你到玻璃店去裁一塊和原來大小一樣的玻璃，你是帶①去，還是帶②去？或者①和②都帶去？學生議論紛紛，說法各一，為后面學習“全等三角形”的判定打下埋伏，堅定學生學習的信心.

■

又如學習“有理數的乘方”，首先分小組交流、探討下面問題：一張紙，厚度0.1毫米，連續將它對折20次，會有多厚？對折100次呢？對折n次呢？引入新課，探究新知. 總之，課堂教學，只要教師全面把握探究教學目的，找準探究性思維訓練與教材內容之間的結合點，就能創設出多種多樣的問題情境，活躍課堂氣氛，達到較好的課堂教學效果.

■ 課堂教學中要有猜想

猜想是對事物變化的一種“猜測”、判斷，沒有經過嚴格的推理和驗證. 教師課堂教學，要精心設計問題，讓學生在學習過程中有猜想，在頭腦中形成一種求知的心理定式.

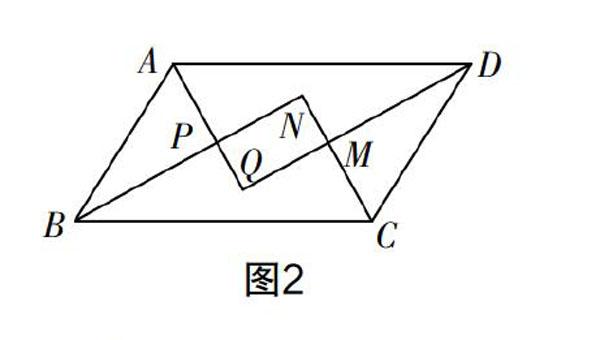
如：已知？荀ABCD中，AQ，BN，CN，DQ分別是∠DAB，∠ABC，∠BCD，∠CDA的平分線，AQ與BN交于P，CN與DQ交于M，在不添加其他條件的前提下，試寫出一個由上述條件推出的結論，并給出證明過程. 這里就要求學生從已知條件出發，沿不同方面、不同層次進行觀察與猜想，從而探索、推理出最理想的結論.

■

再比如：32-12=8×1=8，52-32=8×2=16，72-52=8×3=24，

92-72=8×4=32， …

觀察上面的等式，你能發現什么規律？用代數式表示為______.

猜想的思維基礎是不完全歸納，即由特殊到一般的推理. 教師引導學生猜想越合理，解題思路就越明確.

■ 課堂上有驚訝

教師要善于釋疑學生的迷惘，輕輕點撥后使學生茅塞頓開，心里驚嘆不已，驚訝中有說不出的喜悅之情.

在上“一元二次方程”時，學生對方程的初步知識，在小學就有些基礎，教師如果照本宣科，效果甚微. 抓住學生的好奇心，采取以下方法，可以較好地調動學生的學習積極性：每位同學設自己的歲數為x歲，請你用自己的歲數，乘以2，再加上5（這個過程要求學生獨立完成）. 接著，教師隨意叫幾位同學報出結果，教師故意想一想，說出學生的歲數，使學生在驚訝中思索：老師怎么這么快就知道我的歲數？心里驚嘆，加深了求知的欲望. 教師抓住時機，引入新課，發展學生的思維.

■ 課堂上應有笑聲

教師的教學、講述，要生動有趣，幽默詼諧，使得學生不時地會心一笑，活躍課堂氣氛. 我們都知道，數學離不開數字、圖形，如果沒有教師的課堂氣氛調動，一節課下來往往就是死氣沉沉，久而久之，學習上兩極分化就會很嚴重. 教師應該善于聯系生活實際，多挖掘生活中的趣事，使學生的核心素養得到更好的體現.

如教學“倒數”時，可以通過“翻跟斗”——單杠運動，加深學生的理解，使問題變得生動、形象. 學習“有理數”的有關定理及法則時，告訴學生，這些內容，猶如生活中的法規，如果你不去遵守，違反了，就要造成重大錯誤，使學生從中知道平時學習時應該照章辦事，格式規范，一絲不茍.

又如學習“合并同類項或同類根式”，如何化簡3a2-2b+5a2-4b+3？對此，可以打個比方：團結友愛、性格相合的人，經常性一下課就會在一起，談學習，談理想. 正如上面式子中的3a2與5a2，-2b和-4b，它們都有共同點，含有相同的字母和次數，是一對好朋友，可以走到一起，引出3a2-2b+5a2-4b+3=（3a2+5a2）+（-2b-4b）+3，很好地完成了這部分知識的學習，學生在愉快的氛圍中掌握了知識要點.

■ 課堂應有爭議

爭議可以使數學問題從惘然中得到順利解決. 教師要鼓勵學生大膽質疑，讓學生圍繞數學問題各抒己見，把問題弄明白.

如，（1）有理數乘法運算的學習，教師把（-3）×（-7）-6×（-9）做如下板書：

①（-3）×（-7）-6×（-9）=21-6×（-9）=15×（-9）=-135;

②（-3）×（-7）-6×（-9）=21-54=-33.

學生針對教師的解題思路，展開激烈討論;教師抓住時機，讓學生說一說自己的解題思路，使得問題順利解決.

（2）絕對值概念教學，比較抽象，是數學教學的一大難點. 學生對一些實際數字求絕對值，能較好地掌握，但遇到“已知a<0，b>0，且a>b，那么a+b與0的關系是什么”等類型題目時，學生不知所措. 這時教師就要以學生為主體，讓學生爭議，大膽質疑，緊扣“同號”與“異號”，結合絕對值概念，提醒學生多舉實際數字，通過計算、比較，把問題弄清楚.

■ 課堂上有沉思

一節課，學生要有思考的余地;在一些關鍵問題上，教師要留有“空白”，多讓學生獨立思考，自主交流、探討. 學生的學習，教師的引導，應相輔相成. 好的教育，強調教師的教是為了不教，目的就是讓學生有良好的學習習慣、頑強的探索精神、創新的學習方法.？搖

如教學“二次函數”表達式的多樣性，教師一定要讓學生自己動手，獨立按配方、描點、連線進行練習，積極思考，加深理解;從中滲透平行移動的思想，知道確定一個二次函數的圖像，關鍵在于確定開口方向、頂點坐標-■，■■及對稱軸x=-■.

■ 讓學生有聯想空間

教師講課，應留有余地，讓學生產生聯想，透過有限去展現無限，讓學生思維更寬廣，激發興趣，開拓創新.

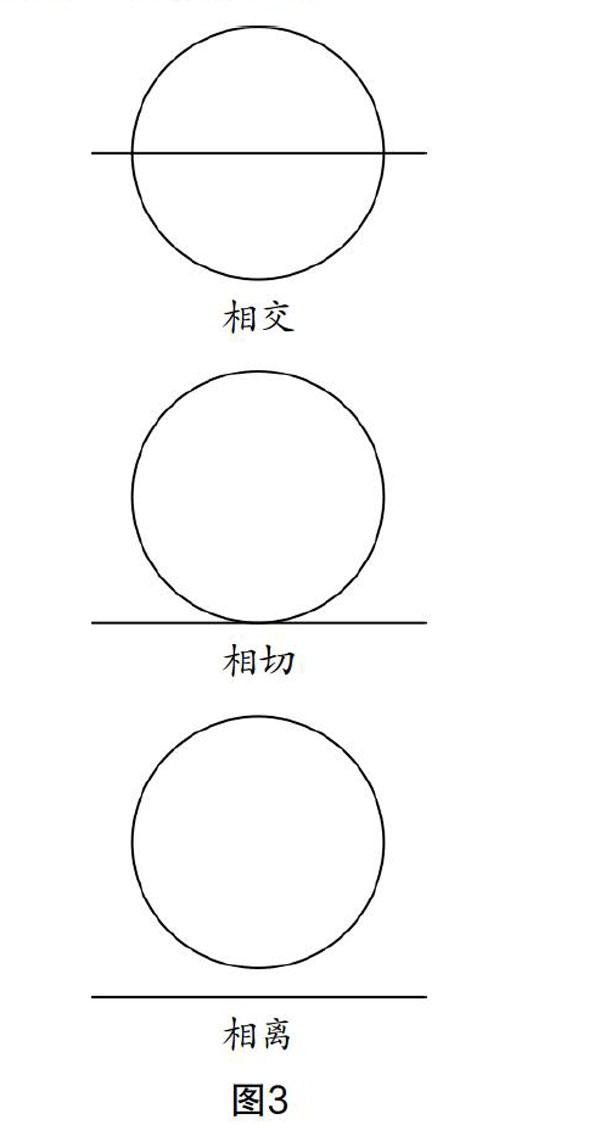
“圓”是初中數學教學的重點、難點，需要教師創新教學方法. 在分析、講解這一章知識點時，教師可發揮學生的主體作用，通過聯想去掌握有關知識. 如講解“直線與圓的位置關系”，可以引導學生聯想太陽與地平線的位置關系：剛剛露出一點→脫離地平線慢慢升起→西落. 學生根據這一規律，畫出圖形，理解三種位置關系.

■

教學“圓與圓的位置關系”可以引導學生聯想“奧運五環”、宇宙空間的“星球”的位置關系.

聯想的思維基礎是類比推理，既由特殊到特殊的推想，把解決某個特殊問題的原則和方法“移植”過來，應用在接近或者相似的問題上，聯想的方法不同，得到的解決方法也不同.

聯想是探索解題途徑的一種基本方法.

■ 結語

教學是一門藝術，教無定法. 課堂氣氛的活躍，需要及時創新教學方法，培養學生的綜合能力. 教師在教學中，應充分調動學生的積極思維，運用各種手段，向學生提出更高的思維要求，促進學生自主發展.