例談促進深度思考的數學教學策略

王慧云

摘要：數學教學應該促進學生深度思考、發展思維。對此，可以有如下策略：以問題情境，促進學生主動地思考;以模型建構，促進學生數學地思考;以連環追問，促進學生深度地思考。

關鍵詞：數學思維;深度思考;問題情境;數學模型

數學是思維的科學，是“思維的體操”。數學教學應該促進學生深度思考，進而發展思維。對此，可以有如下策略：

一、以問題情境，促進學生主動地思考

情境蘊含、產生問題，問題驅動、引領思維。為了促進學生深度思考，可以創設適當的問題情境，促使學生情智在場、具身投入，主動地思考。

例如，教學蘇教版小學數學四年級下冊《多邊形的內角和》一課，可以設計如下逐步遞進的探究問題，不斷驅動、引領學生主動地思考：

（1）看到這一課題，你想到了什么？（明確學習起點）

（2）對于多邊形的內角和，你想知道些什么？（明確學習任務）

（3）面對這些問題，你覺得該如何有序地開展研究？從哪種圖形入手？（明確研究方向）

（4）回顧一下，我們研究三角形的內角和時，采用了哪些方法？這些方法對今天的學習有哪些借鑒呢？（明確研究思路）

（5）你已經知道了哪種四邊形的內角和？是多少度？你覺得一般四邊形或者說任意四邊形的內角和會是多少度呢？（明確常規方法）

（6）除了量和拼，我們能否換個思路，想想還有其他的方法嗎？既然我們已經學過三角形的內角和是180度，那么能否把四邊形分割、轉化成三角形呢？最少能轉化成幾個？

（7）和剛才量、拼的方法比起來，你覺得這種分割的方法如何？如果給你任意一個四邊形，你會用這種分割的方法得出它的內角和嗎？

（8）我們已經通過分割成三角形的方法得到四邊形的內角和是360°，順著這樣的方法和結果，要求五邊形、六邊形、七邊形……的內角和，其實就是要看什么？

（9）這些多邊形應該怎樣分割，各分割成多少個三角形，才能方便地算出它們的內角和呢？其中是否存在某種規律？

（10）通過實踐操作和數據整理，你發現了什么規律？如果圖形的邊數越來越多，你能根據發現的規律求出它的內角和嗎？你能用一個式子表示多邊形內角和的計算方法嗎？

……

二、以模型建構，促進學生數學地思考

數學是模式（模型）的科學。模型思想注重運用數學知識解決問題（尤其是現實問題），且追求將一個問題的解決拓展為一類問題的解決。《義務教育數學課程標準（2011年版）》指出：“（運用數學知識解決問題的）活動應體現‘問題情境—建立模型—求解驗證的過程，這個過程要有利于理解和掌握相關的知識技能，感悟數學思想，積累活動經驗;要有利于提高發現和提出問題的能力、分析和解決問題的能力，增強應用意識和創新意識。”為了促進學生深度思考，教師還可以引導他們建立模型，促使他們理解本質、掌握方法，學會數學地思考。而引導建立模型，要讓學生經歷從模仿到創造的循序漸進、先立再破、不斷提升的過程。

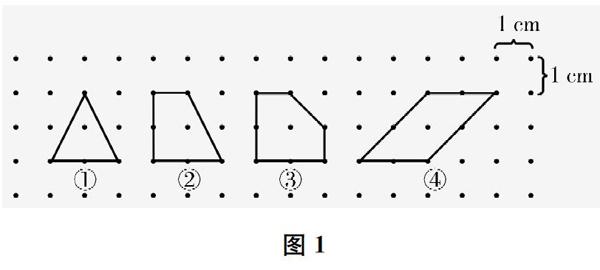
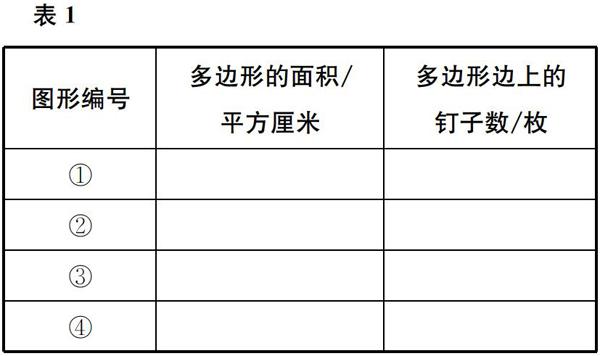
例如，教學蘇教版小學數學五年級上冊《釘子板上的多邊形》一課，可引導學生通過觀察、操作、推理、計算，不斷地尋找關系、發現規律，建立不同層次的模型：

首先，引入圖形面積計算的常規方法后，出示圖1和表1，提出問題：下面多邊形的面積各是多少平方厘米？每個多邊形邊上的釘子各有多少枚？先數一數、算一算，將結果填入表格中，再與同學說說你的想法。學生探究后發現：這些多邊形邊上的釘子數越多，面積就越大;這些多邊形面積的數值（平方厘米）是邊上釘子數的一半;這些圖形還有一個共同的特點，就是內部都只有1枚釘子。進一步地，學生總結出多邊形內部只有1枚釘子時，它的面積（數值）與邊上的釘子數的關系：多邊形的面積=邊上的釘子數÷2——用n表示多邊形邊上的釘子數，用S表示多邊形的面積（數值），那么S=n÷2。由此，建立知識上最初級的模型。

在此基礎上，繼續提出問題：（1）研究到這里，你能想到什么？（2）如果多邊形的內部有2枚、3枚、4枚……a枚釘子，會有什么樣的規律呢？（3）如果多邊形的內部沒有釘子呢？通過探究，學生逐漸發現并總結出其中的規律：設a為多邊形內部的釘子數，則a=2時，S=n÷2+1，a=3時，S=n÷2+2，a=4時，S=n÷2+3，a=5時， S=n÷2+4，a=0時，S=n÷2-1——用一個公式概括就是S=n÷2+a-1，即皮克定理。由此，建立知識上更高級的模型。

然后，提出問題：回顧探索、發現規律的過程，你有什么體會？通過交流碰撞，學生梳理歸納出：（1）要善于從不同的多邊形中找到它們的相同點;（2）用含有字母的式子表示規律，簡明易記;（3）探索規律時，要認真觀察、反復比較，而發現規律后，要進行驗證。由此，建立方法上更高級的模型（范式）。這一模型不僅適用于本節課的探究，而且適用于今后許多數學知識的學習。

三、以連環追問，促進學生深度地思考

數學思維需要經過不斷琢磨（反復斟酌、推敲），向更深處漫溯，從而做到精益求精，找到知識理解的適切方法、問題解決的不同策略。為此，要多提“……是什么”“……為什么”“……怎么樣”“如果不……還可以……”等指向深度思考的問題。

（一）在思維生長點琢磨

思維的生長點是指可以由此及彼延伸聯系的思維內容。通常，對已有的知識、問題等預設的生長點，可以這樣引導學生琢磨：（1）新知識是在哪些知識的基礎上產生、發展的？新知識“新”在哪里？其本質（特點）與用途（優點）分別是什么？（2）問題的解決，是從條件出發順向思考更簡單，還是從問題入手逆向思考更容易？需要列表整理條件，還是畫圖理解題意？需要合情推理，還是精準計算？而對新穎的思路、想法等生成的生長點，可以這樣引導學生琢磨：這一思路或想法新穎在哪里？巧妙在哪里？給了我怎樣的啟迪？

例如，教學蘇教版小學數學五年級下冊《分數的意義》一課，基于“學生在三年級初步認識了分數，知道把一個物體或幾個物體組成的一個整體平均分成幾份，其中的1份或幾份可以用幾分之一或幾分之幾來表示”的學情，可以這樣引領學生琢磨：（1）除了“一個物體或幾個物體組成的一個整體”平均分后可以用分數表示之外，還有其他情況可以用分數表示嗎？（2）一個物體、一個計量單位或幾個物體組成的一個整體都可以用什么來表示？稱之為什么？（3）自然數“1”和單位“1”之間有怎樣的聯系和區別？（4）什么是分數？什么是分數單位？分數和整數之間有怎樣的聯系和區別？（5）為什么要學習分數？由此，學生會對“分數的意義”有較為充分的理解和深刻的建構。

（二）在思維困惑點琢磨

思維的困惑點是指感到困惑不解的思維內容。通常，對學生思維的困惑點，教師可這樣引導學生琢磨：是沒有理解知識，還是不會操作實踐？是不會舉例驗證，還是欠缺邏輯推理？是思維過于機械、僵化，還是鉆進了牛角尖？

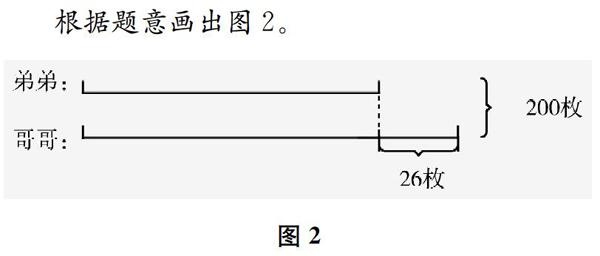
例如，教學蘇教版小學數學四年級下冊《解決問題的策略——畫圖》一課，通過教材例題“小寧和小春共有72枚郵票，小春比小寧多12枚。兩人各有郵票多少枚？”的學習，學生初步理解了畫圖能使數量關系表示得更直觀、更清楚。但是，面對“哥哥和弟弟共有200枚郵票，哥哥給弟弟26枚后兩人的郵票一樣多。哥哥、弟弟原來各有郵票多少枚？”這一變式問題，不少學生誤認為哥哥只比弟弟多26枚郵票，會這樣解題：

根據題意畫出圖2。

因此，弟弟：（200-26）÷2=87（張）;哥哥：（200+26）÷2=113（張） 。

這時，教師可以引導學生琢磨：“哥哥給弟弟26枚后兩人的郵票一樣多”說明了什么？學生經過深入思考，便會明晰：哥哥應該比弟弟多2個26枚郵票，那么，從總數200中去掉2個26，就得到弟弟原有郵票數的2倍，再除以2，就得到弟弟原有的郵票數;在總數200的基礎上添加2個26，就得到哥哥原有郵票數的2倍，再除以2，就得到哥哥原有的郵票數。

在此基礎上，教師可以進一步出示對比問題：“哥哥和弟弟共有200枚郵票，哥哥去掉26枚后兩人的郵票一樣多。哥哥、弟弟原來各有郵票多少枚？”讓學生繼續琢磨：這兩題在結構上有哪些相同的地方？有哪些不同的地方？在解決思路上又有哪些異同？對我們的數學學習有什么啟迪？這樣，學生就會有撥云見日、豁然開朗的感覺。

（三）在思維發散點琢磨

思維的發散點特指可以從不同的角度、向不同的方向發散聯系的思維內容。尤其是在解決問題時，教師可以引導學生發散思考，力求一題多解：除了教材中給出的方法或老師講解的方法之外，是否還有其他的思維路徑和解題方法？而在解決問題后，教師可以引導學生發散思考：得到的結果能否做進一步推廣？

例如，教學蘇教版小學數學四年級上冊《解決問題的策略——列表》一課，解決教材“練習九”第5題（見圖3）時，可以引導學生發散思考，從不同角度分析數量關系，找到不同解題思路。可這樣提問：（1）“照這樣計算”是什么意思？（2）要求“45分鐘生產多少個”，數量關系式是什么？（3）要求“生產540個需要多少分鐘”，數量關系式是什么？（4）如何列式計算這兩問？分別有幾種解題思路與列式方法？分別選用表中的哪一組數量？為什么可以這樣選擇？由此，使得學生明白解題思路與列式方法的多樣性。對第一問，既可以先求出每分鐘生產零件的個數，即工作效率，再用“工作效率×工作時間（45分鐘）”求出工作總量，也可以先求出45里面有幾個3（或6、9），再用得數去乘54（或108、162）。對第二問，既可以先求出每分鐘生產零件的個數，即工作效率，再用“工作總量（540個）÷工作效率”求出工作時間，也可以先求出540里面有幾個54（或108），再用它去乘3（或6）。由此，學生的理解會更深入，思考會更靈活。

（四）在思維聚焦點琢磨

思維的聚焦點特指思維發散后可以通過比較進行優化的思維內容。其實，數學思考既追求多樣的角度和方向，以提升靈活性，更追求優化（適當乃至最佳）的路徑和方法，以提升深刻性。因此，教師要引導學生對因發散而產生的思路和想法進行比較、優化。

例如，教學蘇教版小學數學四年級上冊《解決問題的策略——列表》一課，解決教材“練習九”第5題（見圖3）第二問“生產540個需要多少分鐘？”時，學生通過發散思維，得到兩種解題思路（見上文），進而得到8種綜合列式方法：（1）540÷（54÷3）;（2）540÷（108÷6）;（3）540÷（162÷9）;（4）540÷（216÷12）;（5）540÷54×3;（6）540÷108×6;（7）540÷162×9;（8）540÷216×12。對此，教師可以引導學生聚焦思維，通過比較分析、估算判斷，發現：因為540里面有10個54，所以生產540個零件需要10個3分鐘，即30分鐘。這種思路更加容易理解，這一方法更便于計算。

參考文獻：

[1] 鄭毓信.小學數學教育的理論與實踐——小學數學教學180例[M].上海：華東師范大學出版社，2017.

[2] 王永春.小學數學與數學思想方法[M].上海：華東師范大學出版社，2014.

[3] 曹培英.跨越斷層，走出誤區：“數學課程標準”核心詞的解讀與實踐研究[M].上海：上海教育出版社，2017.