直觀想象：賦予兒童數學思考的力量

【摘 要】直觀想象對于發展兒童的數學思考具有重要價值，它有助于激發兒童獨立自主的學習意識，培養兒童科學有效的思維方式，喚醒兒童實踐創新的理性精神。教師在教學中注重引導、幫助和鼓勵兒童溝通數形聯系、構建直觀模型、創新探究模式，有利于培養他們理性思考的品質。

【關鍵詞】直觀想象;數學思考;理性精神;數形聯系;直觀模型;探究模式

【中圖分類號】G623.5【文獻標志碼】A【文章編號】1005-6009（2020）25-0037-04

【作者簡介】蔣太金，江蘇省連云港市和安小學（江蘇連云港，222000）教師，一級教師，連云港市教學標兵。

良好的數學教育不僅要傳授知識、培養技能，還要發展學生的思維能力和創造能力，提升學生的理性思維、審美智慧和創新精神，更要讓學生經歷數學發現的過程，學會數學地思考問題。數學思考是數學學習的基礎和核心，是數學教學中最有價值的行為，是數學課堂教學的生命力之所在。

一、當下兒童的數學思考存在缺位問題

數學思考，就是指在面臨各種現實的問題（包括非數學問題）情境時，能夠從數學的角度去思考，自覺應用數學的知識、方法、思想和觀念去發現其中存在的數學現象和數學規律，并能運用數學的知識、思想和方法去解決問題。

然而，在當下的數學教學中，兒童的數學思考存在一些缺位現象。例如：在數學學習中，一些學生的表現消極、被動，缺少自主學習的興趣和意識，他們在遇到問題時想的不是去探究、去發現，而是“游離”在一邊，不去思考或假裝思考;在數學交流中，很多學生的思考往往停留在淺表層面，主要是由于學習體驗不到位，缺少實踐反思，缺乏對問題本質的深層分析;在數學探究中，有些學生的學習方式和思維方式單調而低效，在遇到問題時，他們的思考或支離破碎、沒有頭緒，或天馬行空、漫無邊際，缺少方法的積累和思想的沉淀。

二、直觀想象對培養兒童的數學思考具有重要價值

直觀想象是指借助幾何直觀和空間想象感知事物的形態與變化，利用圖形理解和解決數學問題的思維過程。它不單是空間想象能力，也不單是數形結合思想，而是多種數學思想、數學能力的發展和融合。直觀想象主要具有以下特征：其一是直觀性，直觀想象是聯結形象思維和抽象思維的紐帶，它既可以借助幾何直觀把現實情境或數學問題抽象成直觀模型，也可以運用空間想象把復雜的圖形表征抽象成可視化的思維模型;其二是思辨性，直觀想象是一個思辨的過程，在這一過程中，需要調動多種感官，從不同的角度進行分析和綜合，將物體的形狀、特征、變化等結合起來，將眼前的物象與心中的意象融為一體，進行深層次加工;其三是創造性，直觀想象帶給兒童的不僅有分析問題和解決問題的思路和方法，還有其背后蘊含的數學思想和學習經驗。由上可知，直觀想象能開闊兒童的學習思路，豐富兒童的學習方式，提高兒童學習的自主性和創造性。

三、以直觀想象促進兒童數學思考培養的教學策略

（一）溝通數形聯系，化抽象為形象，培養兒童數形轉化的意識

1.借形解數，喚醒操作經驗。

數學是抽象的，數學定義的理解、算法的形成、規律的探究等本身就是一個個抽象的思維過程。但兒童的抽象思維能力并未形成，教師應充分借助直觀操作、直觀模擬等為他們提供思考的平臺和“試驗場”，引導他們逐步從直觀模型過渡到數學理解。如教學蘇教版三上《兩位數除以一位數》一課，計算46÷2，相較于探索算法和理解算理，喚醒學生的操作經驗更有意義。教師可以引導學生借助實物或圖形分一分、擺一擺，巧妙地化解算法的抽象，這種真實的操作體驗有利于學生在頭腦中形成清晰的表象，從而實現對算理的透徹理解。然后從直觀操作引出豎式計算。最后將豎式計算與直觀操作進行類比。這一“聯系操作支持理解，再由算法回溯操作”的過程，有助于學生順利實現從動作思維到符號思維的過渡。

2.賦形以數，內化意義建構。

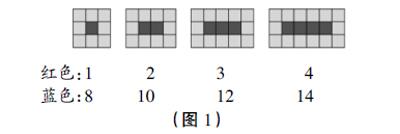
圖形的直觀性為抽象的數學理解帶來了很大的便捷，但有時也需要賦予“形”以“數”的意義，把直觀圖形抽象成具象的數字，從而使兒童理解圖形的本質。如教蘇教版四上《周期規律》一課，教師出示這樣一道練習題：“下面每個圖中各有多少個紅色小正方形和多少個藍色小正方形？照這樣畫下去，第6個圖中的紅色小正方形和藍色小正方形各有多少個？”如果學生只是通過繼續畫圖來尋求結果，那么他們的思考往往只能停留在表層。如果跳出這一“藩籬”，把隱含在圖形中的信息抽象成具體的數字（如圖1），然后先分析數字中的規律，再結合圖形來驗證，反而更容易解決問題。

無論是借形解數還是賦形以數，都是為了在抽象與直觀之間架起一座橋梁，促進學生生成一種數形轉化的思維方式，使他們在遇到一些實際問題時能夠靈活地進行數學思考。

（二）構建直觀模型，化復雜為簡單，提升兒童分析推理的能力

1.搭建操作模型，讓分析游刃有余。

美國教育學家布魯納認為，學生對數學知識的理解有三種模式：一是直觀動作模式，二是具體形象模式，三是抽象邏輯模式。這是一個從動作感知到形象表象再到邏輯抽象的過程。教師教學時搭建操作模型，引導兒童將數學抽象付諸具身體驗之中，既有利于兒童分析和理解問題，也有助于他們實現從形象到抽象的過渡。如教學蘇教版三上《分數加減法》一課，由情境引出算式 + 之后，接下來的探究環節，如果教師直接放手給學生，不少學生會直接將分子相加、分母相加，得出 ，這顯然偏離了探究的主旨和方向。但如果充分利用教材的“情境功能”，引導學生先把長方形的 涂上紅色， 涂上綠色，再寫出算式的得數，學生便能通過涂色和觀察清晰地發現：5個 加2個 得7個 ，是 。操作的過程給學生帶來了真實、深刻的活動體驗，讓學生的分析和理解有了最原始的數學模型。在這一過程中，智慧在學生的指尖流淌，思維在學生的體驗中自然生成。

2.構建圖像模型，讓思考落地生根。

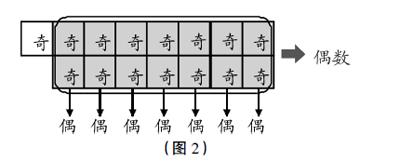
數學的本質特征是其抽象性，抽象的數學知識本身也是兒童認知和理解的難點。在數學教學中，為抽象的數學知識建立起適切的圖像（圖形）模型，引導兒童借助圖像（圖形）的直觀性來學習和審視抽象的內容，他們的思考便有了有力的支撐和清晰的視角，從而能有效地解決問題。如教學蘇教版五上《和與積的奇偶性》，探究之后，學生便能發現：和的奇偶性與加數中奇數的個數有關系。看似完美的結局，實則未能真正凸顯規律的本質。但如果教師此時及時追問：“為什么會這樣呢？”便會激起學生深層次的思考，進而借助圖像（如圖2）分析得出：奇數的個數是奇數，把奇數兩個兩個地湊成一對（即一個偶數），必然還剩下一個奇數，所以和是奇數。直觀的圖像真實地還原了數學問題的本質特點和核心規律，清晰地再現了學生數學思考的過程，學生的學習智慧正在逐步形成。

3.創建思維模型，讓思維拾級而上。

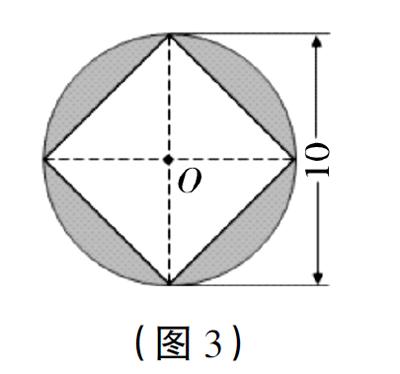
從更開放的視角來看，教師在教學中還應引導學生創建思維模型，充分展現學生思維的全過程。如蘇教版五下“圓”單元有這樣一道習題：求圖（如圖3）中涂色部分的面積。不少學生在解答時感到困難。究其原因，學生的思維是零散的、片面的，他們分析問題時缺乏清晰的脈絡和系統的思考。此時，教師可以引導學生利用思維導圖進行分析（如圖4），讓每一步分析都清晰可見，數學推理也自然形成。環環相扣的思維模型既展現了解題方法，還原了推理過程，也拓寬了學生的思維空間，有助于學生反思意識和學習能力的培養。

（三）創新探究模式，化無章為有法，發展兒童理性思考的品質

1.建構推理模式，讓思考更加靈活。

推理是數學的基本思維方式。推理能力的發展應貫穿于整個數學學習過程中。從推理的角度觀照數學教學，其活動過程就是數學推理的過程。數學直觀能為推理提供模型參照，空間想象能在兒童腦海中勾勒出形象的思維模型和推理路徑。教師在教學中融入推理，讓兒童的學習過程轉變為主動發現、實驗、想象和驗證等活動過程，課堂也會因此增添幾分智慧和靈動。如蘇教版五下“解決問題的策略：轉化”單元有這樣一道練習題：有8支足球隊參加比賽，比賽以單場淘汰制進行。一共要進行多少場比賽才能產生冠軍？學生不難想到，可以畫圖（如圖5）來分析：8支球隊兩兩比賽要賽4場，獲勝的4支球隊再兩兩比賽要賽2場，以此類推，一共要比賽4+2+1=7（場）。其實，分析到這里，教學并沒有結束，教師還應引導學生進一步反思和推理：產生冠軍，就是最后只剩下1支球隊，也就是要淘汰7支球隊，因為每場比賽淘汰1支球隊，所以一共要比賽8-1=7（場）。

2.重構思維模式，讓思想更加自由。

美國心理學家卡羅爾·德韋克指出：人與人之間的差距，就在于思維模式的不同。教師在教學中要關注兒童的心理、態度和習慣，幫助他們樹立正確的學習觀，重建科學的成長型思維模式，不斷激發他們的成長意識和探索精神。如教學蘇教版五下《圓環的面積》一課，學生通過思考大都能發現圓環（如圖6）的面積計算方法，即外圓的面積-內圓的面積=圓環的面積，從而得出π×102-π×62=64π（cm2）。與此同時，一位學生提出了與眾不同的觀點。

生：如果對著圓環剪一刀，我們想象一下，展開來就應該是一個梯形（如圖7）。拼成梯形后，梯形的上底就是內圓的周長，下底就是外圓的周長，高是4米，這樣，梯形的面積為（12π+20π）×4÷2=64π（cm2），和剛才的計算結果是一樣的。

師：同學們覺得她說得有道理嗎？

大部分學生表示贊同，但也有少數學生不認可。教師適時引導學生對上述方法展開討論……

筆者認為，無論學生的發現是否成立，無論他們探究到了何種程度，只要他們認真思考了，就會有自己的理解和感悟。這種獨特的視角、“另類”的表達直接激起的是學生的創新意識，不僅讓學生感受到了成功的喜悅，也成就了他們思維的精彩。

康德曾說：“如果沒有感性，則對象不會被給予;如果沒有知性，則對象不能被思考。沒有內容的思想是空洞的，沒有概念的直觀是盲目的。”要引導兒童進行直觀想象，教師就要給他們提供廣闊的平臺，讓每一個兒童自主地學習、積極地建構、靈活地思考。如此，兒童的可能性被激發，學習意識持續生長，行為習慣持續生成，他們的數學思考也定會精彩綻放。

【參考文獻】

[1]周德明.借助幾何直觀理解問題，構建直觀模型解決問題[J].中學數學，2019（2）：3-9.

[2]戚興棟.立足知識本質，發展學生幾何直觀力[J].數學教學通訊，2018（11）：10-11.

[3]周立棟.小學數學中的推理及其教學[J].上海教育科研，2016（12）：90-92，61.

注：本文獲2019年江蘇省“教海探航”征文競賽特等獎，有刪改。