基于蒙特卡羅模擬的PPP項目投資風險分析

摘要：當前，PPP模式在國內進行得如火如荼，各路資本紛紛摩拳擦掌。對于社會資本參與者而言，需要對投資項目進行諸多評價，尤其是針對收益與風險的財務評價。傳統的投資項目評價模型已發展得非常成熟，有著整套的思路和方法，但對于PPP項目，進行經濟效益分析通常僅從預測來的固定數據著手，鮮有考慮項目面臨的各種風險及存在的眾多不確定性。本文旨在通過對擬投資項目進行蒙特卡羅模擬分析，綜合考慮各方面因素，給PPP投資項目提供一個進行財務評價的新思路。

關鍵詞：PPP項目;投資風險;蒙特卡羅模擬

PPP模式最早起源于歐洲，由政府授權私人資本參與投資建設并運營公共基礎設施，以緩解政府資金吃緊時投資基礎設施建設的壓力。最近幾年，地方政府債務壓力劇增，迫使傳統的工程承包施工模式向投資拉動轉型，再加上財政部的極力推行，更使得這種投資模式在公共基礎設施方面的參與度越來越高。基礎設施領域的投融資模式從地方政府融資平臺主導，逐步向平臺融資為主、PPP模式為輔的局面轉變，有些地方甚至出現兩種融資模式并行的情況。然而，PPP項目整個生命周期存續時間長，項目參與者多，組織結構復雜，面臨的不確定性因素很多，尤其是在項目建成投產后的運營階段，投資者最為關注的莫過于評價和監控項目收益是否已達到預期。

一、風險分析的必要性

在項目實踐中，國內眾多對PPP項目進行投資評價的案例多側重于確定某個價格水平，而現實是，外部環境如政府履約能力下降、材料價格上漲、技術更新、政策變化、產品標準升級等因素的變化，使得一個簡單的道路施工項目都無法按照招標價格完全鎖定，更遑論長達20—30年經營期的PPP項目了。如果投資者在進行投資效益分析時，僅按照某些給定的數據資料進行財務分析和測算，必然與實際存在較大出入，因此，投資前分析擬投資項目的風險和不確定性是非常重要且有必要的。

二、分析方法的選擇

當下，國內對傳統投資項目進行財務評價多參考建設部和發改委發布的《建設項目經濟評價方法與參數》（2006第三版），而PPP作為一種新的投融資模式，尚未形成自有的一套評價體系。在《PPP項目財務評價實戰指南》中，蒲明書等學者以傳統常規投資項目分析評價方法為基礎，初步構建了PPP項目財務評價模型，即根據市場調查與預測得來的數據，在不同層面（項目全投資、項目自有資金、投資各方現金）編制能夠滿足不同分析目的的財務報表，在此基礎上對項目作出評價，來滿足投資各方不同的決策需求。財務分析的基礎是對財務報表進行分析，而評價投資項目的可行性更是依賴于根據項目各期資金流入流出情況編制的預測現金流量表。該書參照方法與參數給出了三個評價PPP項目的指標，包括動態投資回收期、凈現值及內部收益率。

然而，在方法與參數一書中并未補充具體的風險分析及有關的指標評價，《PPP項目財務評價實戰指南》雖然略有提及，但也并未給出具體的處理過程。參閱相關文獻了解到分析項目風險的方法有兩種基本途徑：一是比較傳統的方法，即對相應評價指標做適當修正;二是采用技術分析的方法，如敏感性分析法和概率樹法，但是這兩種方法的缺點顯而易見，它們僅能圍繞單個因素的變動進行分析或只能模擬有限場景，不能對所有可能發生的情況進行測算，并且在復雜的環境條件下，目標值同時受諸多因素的影響，單一因素分析也不能反映具體實際。蒙特卡羅模擬可以同時對多個變量進行成千上萬次模擬，這就相當于整個測算過程中該項目實施了成千上萬次，而輸入的影響目標值的變量如投資總額、折現率、年均現金凈流量則是隨機的，每模擬一次都會給出一個目標值，在此基礎上計算目標值的概率分布圖，同時可以根據計算出來的項目標準差及變異系數確定目標值偏離預期的程度，由此評價目標項目的風險高低。經過考量分析，對PPP投資項目進行財務評價選擇蒙特卡羅模擬方法是合適的。

三、蒙特卡羅模擬分析方法的具體實施

對投資項目進行蒙特卡羅模擬分析：第一，確定目標變量，筆者在此選取的是前述三個評價指標中的凈現值指標;第二，確定影響目標變量的各項經濟因素，并分析各因素的參數特征;第三，確定目標值與各變量之間的影響關系，建立評價指標計算模型;第四，模擬運算，并得出合適數量的樣本值;第五，對樣本值進行統計分析，并對模擬結果進行解釋。

以某河道治理PPP項目為例，蒙特卡羅模擬的分析步驟如下：①根據歷史資料分析相關數據信息，評估相關參數特征，確定概率分布，如項目初始投資額符合正態分布，年均凈現金流符合三角分布，利率（折現率）符合均勻分布，由此產生各參數每次模擬時的隨機數;②建立財務風險評價模型;③進行模擬運算，通過查閱相關文獻，結合項目實際情況，模擬5 000次得到的樣本值足以對項目風險進行客觀分析與評價;④對5 000次模擬得到的樣本值進行統計分析，求出項目凈現值指標的概率分布;⑤分析評價目標項目風險水平和預期盈利能力。

四、案例分析

（一）案例資料

某投資項目為城市河道治理工程，不具備獨立的商業經營條件，采用政府購買服務模式以保證SPV公司合理利潤。項目選擇“股權合作+BOT”的PPP模式，合作期限20年（其中建設期2年，經營期18年），政府在合作期10年內完成社會資本股權回購。20年合作期滿由SPV公司將全部資產無償移交政府指定機構。

1.項目總投資估算約45 413萬元（實際操作中以審計局審計決算值作為政府財政支付的最終依據），其中建設投資43 650萬元，建設期融資費用約1 763萬元。銀行融資費率用按現行五年期以上銀行貸款基準利率即4.9%（隨利率變化而同步調整）。

2.根據政府資金支付的不同用途，政府財政支出按股權回購費用、SPV融資還本付息費以及運營缺口補助費等三部分進行測算。

第一，股權回購費用。按照政府在合作期10年內完成社會資本股權回購（回購方式和比例暫按合作期第6年至第10年等比例回購），資本金內部收益率執行5年期以上銀行貸款基準利率，從而測算社會資本股權回購支付資金。經計算股權合作期10年內政府支付股權回購費用約12 370萬元。

第二，SPV融資還本付息費。貸款期限20年（含建設期2年），貸款償還按照等額還本、利息照付方式，按照5年期以上銀行貸款基準利率4.9%（隨利率變化而同步調整）測算，20年合作期內政府支付SPV融資還本付息費總額約52 352萬元。

第三，運營缺口補助費。不考慮折舊攤銷，按照4.9%年靜態利潤率（執行5年期以上銀行貸款基準利率），以運營成本為基數核算合理利潤，并考慮扣除稅金及附加后，計算運營缺口補助（即運營財政補貼，列入年度財政預算），經核算20年合作期內政府支付運營缺口補助約936萬元。

綜上，20年合作期內政府財政支出總額約65 658萬元（折現值約41 494萬元），包括股權回購費用約12 370萬元，SPV融資還本付息費約52 352萬元，運營缺口補助費約936萬元。

（二）風險因素識別

社會資本方根據政府方提出的合作條件，結合所掌握的相關基礎資料，需要作出是否參與該項目的投資決策。決策中最大的不確定性因素與項目投資總額、資本成本、及年均凈現金流量有關，而后者與運營成本有關。說明如下：

由于政府支付的股權回購金額、融資還本付息費及運營缺口補助金額是固定的，這些作為項目全投資的現金流入不存在政府違約風險以外的、由于不確定性導致流入減少的風險，因此，在進行蒙特卡羅模擬分析時可以不予考慮;在現金流出方面，投資額看似固定，但實際操作中以審計局審計決算值作為政府財政支付的最終依據，而根據經驗數據，由于對項目所處環境了解不足、材料人工費用等成本上漲、施工技術要求提高等因素，導致最終決算金額與前期合同金額存在較大出入的情況非常普遍;另外，本案例投資施工方案中測算每年的運營成本除試運營期外基本穩定在某一固定值，而事實是，在較長的一段時期，運營成本可能與物價指數相掛鉤呈逐年上漲趨勢或圍繞某一固定值上下波動，受這些不確定性因素影響，項目凈現金流出可能會波動上漲而不會是固定在某一特定值上。此外，銀行利率在漫長的經營期內受國家財政政策調整的影響，也不可能被完全鎖定。這些不確定性因素都會影響到項目現金凈流量，進而影響到社會資本方投資該項目的效率與效果。

（三）風險因素的概率分布假定

為作出投資決策，社會資本方需進行項目全投資現金流分析，計算項目全投資的財務凈現值。為反映不確定性因素對項目投資效益的影響，進行蒙特卡羅模擬分析。在蒙特卡羅模擬分析中，將項目總投資、項目折現率與年均凈現金流量均取為輸入變量，項目全投資凈現值取為目標變量，通過蒙特卡羅模擬得到項目全投資凈現值的若干樣本值，進而計算其統計特征量。

在蒙特卡羅模擬中，假定項目總投資符合期望值為45 413，標準差為1 500的正態分布;折現率選用融資成本4.9%，隨銀行利率調整上下浮動，根據利率調整數據資料分析，假定符合3.9%—5.9%的均勻分布;年均凈現金流量根據實施方案測算，假定符合最大值為5 929萬元，最小值2 070萬元，最可能值為3 135的三角分布（三角分布各值由項目施工方案給出的各特定值測算得出）。

（四）選定實現相關參數變量的函數

由于上述參數分別符合正態分布、均勻分布與三角分布，故在EXCEL表格中可以直接采用NORM.INV、RAND（）函數來產生隨機數。在EXCEL中實現三角分布需要固定前一次所取的隨機數以避免數據由于表單操作而發生變化。相關參數的表現形式如下：

1.項目初始投資：C0=NORM.INV（RAND（），45413，1500）

2.折現率：

3.年均凈現金流量：C1=2070+（5929-2070）×IF（RAND（）<

4.項目凈現值NPV：NPV（rate， value 1，value2，……）

（五）模擬運算過程

筆者利用EXCEL進行了模擬運算，涉及的項目初始投資、項目折現率以及年均凈現金流量等數據均由計算機系統隨機產生，每次運算均產生相應的凈現值。對5 000個隨機得來的凈現值進行統計分析，以找尋其統計特征及規律;將凈現值下限設定為0，并對其進行降序排列，計算出凈現值大于0的累計概率;同時，利用EXCEL中的AVERAGE函數及STDEV函數分別求出該組數據的均值及標準差，利用MAX（）及MIN（）函數求出5 000次模擬凈現值的極大值及極小值。

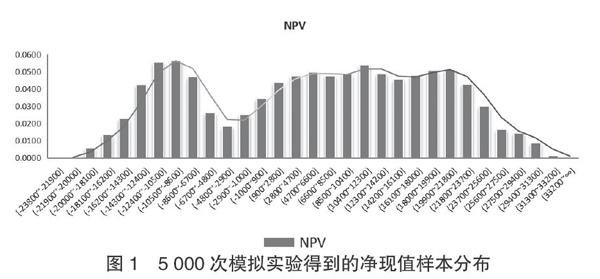
利用該組數據繪制直方圖，就得到了被研究的該PPP投資項目的凈現值樣本分布圖（如圖1）。

本文利用用蒙特卡羅模擬法在計算機模擬5 000次，得到擬投資項目凈現值NPV如下的統計特征：最大值為31 717.13萬元，最小值為-23 243.56萬元，平均值為4 066.16萬元，標準差為12 783.71萬元，凈現值出現在0—31 717.13的概率為62.82%，凈現值出現負數的概率為37.18%。同時，各數據偏離期望值的離散程度很高，該投資項目雖然可行但存在較大風險。

五、結語

本文利用EXCEL軟件提供的函數功能，實現了蒙特卡羅模擬實驗，通過案例給出了基于蒙特卡羅模擬的PPP項目投資風險分析的具體處理過程，并對項目作出評價。然而，本文在處理過程中仍有不足之處，在進行年凈現金流測算時，為了簡化過程，假定各年凈現金流量滿足符合某一數據特征的三角分布，而在該案例中，由于5—10年的股權回購，因而在這一階段凈現金流與其他各年存在較大差異，但本文中給予了模糊處理。

參考文獻：

[1]蒲明書，等.PPP項目財務評價實戰指南[M].北京：中信出版社，2016.

[2]國家發展改革委建設部.建設項目經濟評價方法與參數（第三版）[M].北京：中國計劃出版社，2006.

[3]向壽生，尚宇梅.Excel在投資項目概率分析中的應用[J].商業研究，2008（7）.

[4]梁磊.用EXCEL實現風險決策的蒙特卡羅模擬分析[J].科學技術與工程，2008（20）.

[5]謝嵐.管理會計中EXCEL的高級應用：長期投資決策的蒙特卡羅模擬模型的設計與應用[J].財會信息化，2014（10）.

[6]連春茗，孟昭亮.PPP項目財務評價指標含義及其適用性的比較研究[J].中國工程咨詢，2017（6）.

作者簡介：渠文靈（1987—），女，山東鄆城縣人，會計師，碩士，主要從事財務工作研究。