素養導向下高考導數解答題的備考之道—-2019 年高考全國Ⅰ卷第20 題的試題分析及備考啟示

廣東省佛山市南海區石門中學 劉偉

在2019 屆高考備考中,筆者任教實驗班,承擔了學校尖子生培養的重任.高考備考中應如何突破導數解答題,一直是筆者教學及備考過程中不斷思考的問題.本文中,筆者將結合對2019 年高考全國Ⅰ卷理科數學第20 題的研究,談談自己在導數題備考中的一些思考與體會.

1 試題呈現

已知函數f(x) = sinx-ln(1+x),f′(x)為f(x)的導數.證明：

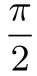
(2)f(x)有且僅有2 個零點.

2 靜觀其“變”

該題的題干十分簡潔,給出一個不帶參數的函數解析式,題目設置兩問,都是零點問題(第一問本質就是二階導函數的f′′(x)變號零點問題).題干十分簡潔,因為不帶參數,給人的第一印象不會太難.但仔細一看,該題還是有很多“與眾不同”的特點：

創新點1—-函數形式新：縱觀近十年全國Ⅰ卷的導數題,基本都是由超越函數或與多項式函數的組合或復合而成的,幾乎沒有出現超越函數與正余弦函數組合而成的高考題,因此該題中出現的函數f(x)=sinx-ln(1+x)會讓學生們感到十分陌生,不知如何下手.

創新點2—-考查方向新：2016 年起,廣東省恢復使用全國1 卷的試題,2016 年及2018 年均考查了二元不等式,備考老師很容易形成一種備考的思維定勢,過分關注二元不等式的相關問題,甚至把它放在導數備考中的首要地位,2019 年各地模擬題中層出不窮的二元(含x1,x2)不等式問題足以反映這種思維定勢.此題考查的方向也與“預估”的不同,有較明顯的反押題反刷題的味道,符合高考的公平性及選拔性要求.

創新點3—-設問形式新……