函數思想下分段計費問題的教學探究

鄭祥旦

（福建省大田縣教師進修學校）

分段計費問題是人教版《義務教育教科書·數學》五年級上冊的教學內容，在后繼學習中可看作分段函數的問題。運用函數思想做好分段計費的教學，需要了解分段教學的基本思想，需要了解學生使用圖象法學習的基礎。

一、了解分段函數的基本思想

分段函數本身不是初等函數，但它是由若干個基本初等函數組合而成的。例如，人教版《義務教育教科書·數學》八年級下冊有如下的一道例題，其中y與x的函數解析式可表示為，其圖象如圖1所示。

圖1

例：“黃金1號”玉米種子的價格為5元/kg，如果一次購買2kg以上的種子，超過2kg部分的種子價格打8折。

（1）填寫下表。

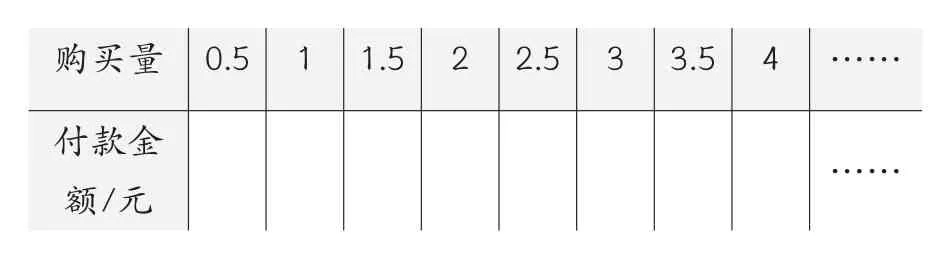
0．5 1 1．5 2 2．5 3 3．5 4 ……購買量付款金額/元……

（2）寫出購買量關于付款金額的函數解析式，并畫出函數圖象。

x＝2是此分段函數的分段點，同時y(x)在x＝2是連續的。而函數的連續性及其相關的證明通常是微積分的內容。

與上題相比，五年級分段計費的例題則是另一種表現形式的分段函數，y與x的函數解析式可表示為

x＝3、4、5、6是此分段函數的分段點，y(x)在x＝3、4、5、6上也是連續的（如圖2）。

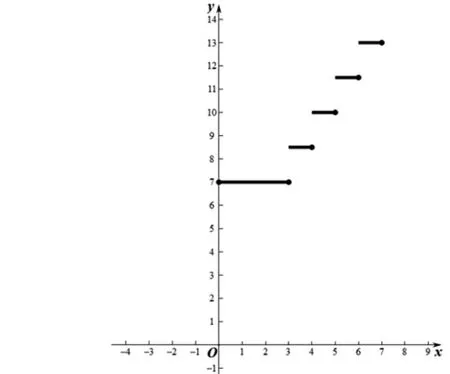
圖2

其圖形在x＝3、4、5、6各點產生跳躍現象，我們稱x＝3、4、5、6為函數y(x)的跳躍點。

顯然，學生畫出這樣的圖形是不符合題意的（如圖3），該圖形用函數解析式表示為：

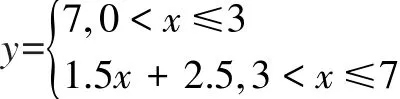
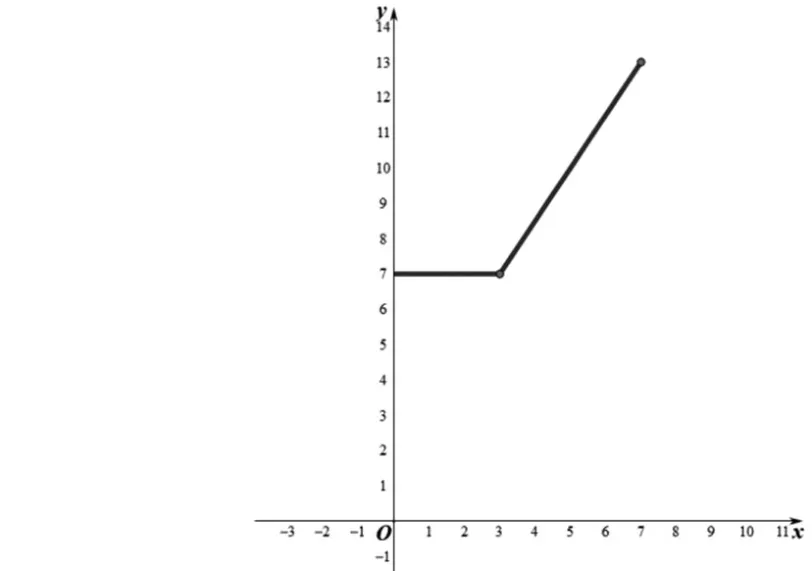
圖3

進一步來說，分段計費的例題是由若干常量函數組合而成的分段函數，學生畫出的圖形是由常量函數和正比例函數組合而成的，而八年級所學的則是由兩個不同的正比例函數組合而成的。但這樣的題目也存在于五年級的練習題，如“某市自來水公司為鼓勵節約用水，采取按月分段計費的方法收取水費。