數形結合思想方法在高中數學教學與解題中的應用

盛福明

摘 要隨著我國新課標的推進和落實，為進一步提升學生的綜合能力，必須要不斷激發出學生的學習興趣，幫助學生養成獨立自主的學習能力。在教學過程中，數學教師們必須要使學生掌握一定的解題思路和方法，因此可采用數形結合的方式，運用在高中數學教學以及解題中，提升學生數學學習以及解題效果。

關鍵詞數形結合;高中數學;教學;解題

中圖分類號：C41 文獻標識碼：A 文章編號：1002-7661（2020）08-0065-01

當前我國的教育水平正在不斷完善和提高，由于受到長期應試教育的影響，傳統的教學模式已經無法滿足當前的教學需求，教師要將課堂歸還給學生，使學生成為課堂上的主體。高中數學的學習需要學生具備較強的邏輯思維能力和理解能力，要想使學生對抽象的數學概念和知識有更好地吸收和理解，可以將數形結合的思想方法融入其中，循序漸進地提升學生的解題能力。

一、數形結合思想“數轉形”的運用

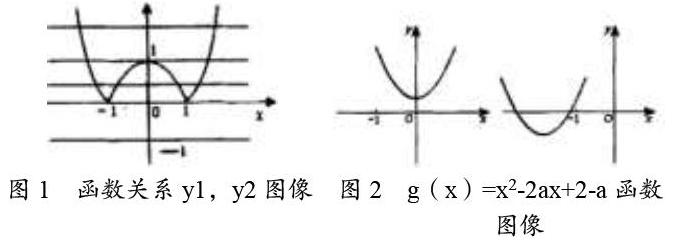
在高中的數學學習中具有較多形象且直觀的圖形，這些圖形對幫助學生解題以及教學都有很好的輔助作用，所以在實際的教學過程中，教師可以引導學生通過數形結合思想去解決難以求解的代數以及抽象的數學問題，為幫助學生找出解題思路，加強學生的數學邏輯，可以通過圖形激發學生的具象思維。例如，在講解︱x2-1︱=k+1中求K的取值，教師可以將方程轉變為y1以及y2不同函數，得出y1=k+1，y2=x2-1，教師可以引導學生繪制函數圖像。如圖1所示，函數關系式y1=k+1在坐標系中與x軸平行的直線，因此：（1）k<-1時，y1以及y2無交點，故原方程無解;（2）k=-1時，y1，y2則有兩個交點，因此原方程有兩個解;（3）若-1

二、數形結合思想中“形轉數”的運用

解答高中數學題的過程中，圖像和圖形能夠起到很好的輔助作用，但這須要學生自身具備較強的邏輯思維能力，若是對其中的數學知識點掌握不熟悉，單純依靠圖形解決問題也很容易出現錯誤。在解題中需要靈活運用數形結合，為防止不必要的失誤，可通過“形”轉“數”的方式解決代數問題，從而拓寬解題思路。例如，在解答函數f（x）=x2-2ax+2中，當x∈[-1，±∞]，函數f（x）=x2-2ax+2>a成立，求函數a的范圍。通過題意可得出當x∈[-1，±∞]時，函數g（x）=x2-2ax+2-a處在直角坐標系橫軸，及x軸的下側，如圖2所示，若使等式成立，需保證a∈（-2，1）或a∈（-3，1）.

圖1 函數關系y1，y2圖像圖2 g（x）=x2-2ax+2-a函數圖像

類似于這類題目就需要學生通過形轉數的方式，把函數圖像轉變為代數問題進行解決，同時要抓住題干中的已知條件，不能忽略已知限定變量，確保形轉數的高效。

三、數形結合思想中數形轉換的運用

在高中數學課堂上學生需要靈活運用數形轉換，例如針對于一些靜態函數的解答，就可以將數形轉換運用其中，對高中數學中的一次函數、二次函數以及三角函數等較為抽象的問題進行分析，并且這種數形轉換能夠解決圓錐曲線以及直線等問題。

四、數形結合思想要與教材相融合

高中的數學知識教學有許多都離不開數形結合思想，例如，教師在對“不等式的求解”知識內容教學時，除了采用傳統的方式進行解答之外，教師還可以通過數形結合思想中的“形”解答，將其中的絕對值賦予幾何意義。除上述之外，為了能夠更廣泛的貫徹數形結合，教師可以采用樹狀圖的方式將可能存在的答案都一一列舉出來。這樣能夠便于學生更好地理解和接受，同時能夠防止學生出現記憶混亂的情況。

函數知識一直都是高中數學較難的部分，其中的冪函數、三角函數都讓學生感到頭疼。在解答此類數學題時需要結合題干以及直角坐標系，在坐標系中將題干中的文字描述通通體現出來，通過將復雜的問題簡單化，解出問題的答案。教師應當將類似的方法傳授給學生，使學生掌握解題方法培養自主學習的能力，從根本上提升學生的綜合素質。

綜上所述，數形結合包含了形轉數、數轉形等方法，是高中數學教學和解題常用的方法之一，為了能提升高中生的解題效率，教師須要潛移默化的使學生掌握數形結合思想，通過空間圖像變換、數量關系等解決問題，同時結合抽象和具象思維提高高中數學的解題能力。

基金項目：本文系2018年度甘肅省“十三五”教育科學規劃一般自籌課題《活用“數形結合”思想提高高中學生數學解題能力的研究》成果之一，課題立項號GS[2018]GHB1866。

參考文獻：

[1]鄢爭艷.數形結合思想在高中數學教學中的應用[J].數碼設計（下），2019（10）：103.

[2]趙順林.數形結合在高中數學教學中的運用探究[J].讀與寫，2019（27）：186.