題組

摘 要：學(xué)生的學(xué)習(xí)深度不夠，學(xué)生的學(xué)習(xí)只停留在熱鬧的表層，并沒(méi)有通過(guò)學(xué)習(xí)達(dá)到知識(shí)的深度建構(gòu)，沒(méi)有將知識(shí)內(nèi)化為自身的能力和素養(yǎng)。因此教學(xué)中要關(guān)注題組的練習(xí)，只有高質(zhì)有效的題組練習(xí)，才能讓學(xué)生既有進(jìn)一步學(xué)習(xí)的興趣，又能通過(guò)練習(xí)讓學(xué)生對(duì)知識(shí)有更深入的本質(zhì)理解，從而完成知識(shí)的建構(gòu)，形成真實(shí)的數(shù)學(xué)素養(yǎng)。

關(guān)鍵詞：題組;練習(xí);深度學(xué)習(xí)

一、 梯度呈現(xiàn)，讓感悟更深刻

數(shù)學(xué)題如果只是零亂地呈現(xiàn)知識(shí)的話(huà)，學(xué)生通過(guò)學(xué)習(xí)只是得到了一些零碎的知識(shí)點(diǎn)。因此題組的呈現(xiàn)要讓學(xué)生能更好地完成知識(shí)的獲取和技能的形成，更要能讓學(xué)生從題組的練習(xí)中經(jīng)歷數(shù)學(xué)問(wèn)題的抽象和構(gòu)建數(shù)學(xué)模型的全過(guò)程，在數(shù)學(xué)的學(xué)習(xí)過(guò)程中增強(qiáng)對(duì)知識(shí)的感悟與體驗(yàn)。因此，在組織學(xué)生進(jìn)行新課學(xué)習(xí)時(shí)，可以將知識(shí)以題組的形式有梯度地呈現(xiàn)給學(xué)生，帶領(lǐng)學(xué)生圍繞著遞進(jìn)型題組展開(kāi)學(xué)習(xí)。向?qū)W生充分展現(xiàn)問(wèn)題的產(chǎn)生、發(fā)展和解決方法的內(nèi)在聯(lián)系，除了使學(xué)生學(xué)得解決單個(gè)問(wèn)題的方法之外，還可以通過(guò)幾個(gè)問(wèn)題之間的聯(lián)系以及解決方法的變化，以達(dá)到對(duì)數(shù)學(xué)本質(zhì)知識(shí)的掌握和對(duì)思維的訓(xùn)練。在學(xué)習(xí)中引導(dǎo)學(xué)生關(guān)注數(shù)學(xué)知識(shí)背后的模型，培養(yǎng)學(xué)生建模的意識(shí)，以使得學(xué)生學(xué)習(xí)更有體驗(yàn)，探究更有深度，在題組練習(xí)的推進(jìn)中讓學(xué)生學(xué)會(huì)數(shù)學(xué)建模。

如在乘法分配律的教學(xué)中，由于乘法分配律有乘法和加法兩級(jí)運(yùn)算，并且還包含了括號(hào)的變化，對(duì)小學(xué)生來(lái)說(shuō)是很容易和乘法交換律混淆的知識(shí)。因此在學(xué)習(xí)過(guò)程中需要給學(xué)生提供更容易感知的學(xué)習(xí)素材，這樣才能有效支撐學(xué)生的體驗(yàn)和認(rèn)知。使得學(xué)生不會(huì)只停留在公式的記憶中，知其然而不知其所以然。因此在教學(xué)中可以先出示：（5+15）×3 8×6+12×6 （13+7）×4 5×3+15×3 （8+12）×6 13×4+7×4 思考①：不計(jì)算你會(huì)怎么分類(lèi)？計(jì)算后再分類(lèi)你又會(huì)怎么分？經(jīng)過(guò)學(xué)生逐層遞進(jìn)的分類(lèi)，原來(lái)散開(kāi)的題目就分成兩列，一列有括號(hào)一列沒(méi)有括號(hào)并且左右兩列結(jié)果相等的一一對(duì)應(yīng)的排列在一起，學(xué)習(xí)就此展開(kāi)。接著思考②：對(duì)比左右兩列的算式，你有什么發(fā)現(xiàn)？學(xué)生接下來(lái)都會(huì)發(fā)現(xiàn)有括號(hào)的式子先算和再乘一個(gè)數(shù)，而沒(méi)括號(hào)的先算兩個(gè)乘再把兩個(gè)積相加。這樣學(xué)生就初步建立了對(duì)乘法分配律感性認(rèn)知。再接著思考③：是不是所有這樣寫(xiě)的兩算式都相等呢？你能舉例驗(yàn)證嗎？這樣學(xué)生在練習(xí)的過(guò)程中進(jìn)一步增強(qiáng)了知識(shí)的認(rèn)知。然后思考④：你能用你喜歡的方式表達(dá)這個(gè)規(guī)律嗎？通過(guò)讓學(xué)生借助題組練習(xí)逐步抽象，學(xué)生對(duì)乘法分配律有了更深的體驗(yàn)和感悟，建構(gòu)起數(shù)學(xué)的模型就堅(jiān)實(shí)多了。

二、 同質(zhì)變形，讓知識(shí)能溝通

在一些重要知識(shí)點(diǎn)，我們可以通過(guò)題組的變式，讓學(xué)生在不同的情境中體驗(yàn)相同的知識(shí)加深對(duì)知識(shí)的理解。正是如此在教學(xué)中利用習(xí)題的變形組合，讓學(xué)生在變化的題組練習(xí)中對(duì)知識(shí)進(jìn)行學(xué)習(xí)理解。這樣對(duì)知識(shí)的學(xué)習(xí)就不會(huì)停留在概念的一些關(guān)鍵語(yǔ)句上，而是對(duì)知識(shí)內(nèi)涵有了真正的理解。小學(xué)數(shù)學(xué)分為兩個(gè)階段，隨著學(xué)段的增加，知識(shí)的難度在不斷加大，不少新知識(shí)與舊知識(shí)既有聯(lián)系又有區(qū)別，有時(shí)思維方式會(huì)完全相反。如小學(xué)生在學(xué)習(xí)方程時(shí)，領(lǐng)悟方程的思想是有一定難度的。因?yàn)榉匠痰乃枷牒蛯W(xué)生算術(shù)思維不一致，學(xué)生的學(xué)習(xí)就變得非常艱難。如果老師圍繞著“含有未知數(shù)的等式是方程”這一概念對(duì)方程進(jìn)行判斷理解，這樣展開(kāi)的數(shù)學(xué)教學(xué)就缺乏對(duì)知識(shí)內(nèi)涵的深刻理解。方程背后隱藏著更為重要的思想意義：通過(guò)未知數(shù)參與的等號(hào)左右兩邊表示的兩件事情等價(jià)這一內(nèi)涵的理解就無(wú)法落到實(shí)處。

其實(shí)方程和方程思想一直隱藏在學(xué)生在生活和學(xué)習(xí)中，我們要通過(guò)有效的提煉讓方程和方程思想以題組的形式呈現(xiàn)在學(xué)生的面前，通過(guò)學(xué)生的自主學(xué)習(xí)，使得方程思想更好地納入學(xué)生的數(shù)學(xué)知識(shí)系統(tǒng)之中。在方程的認(rèn)識(shí)教學(xué)中可以呈現(xiàn)這樣的內(nèi)容：①公交車(chē)上原來(lái)有12人，到了一個(gè)站點(diǎn)，上來(lái)3人，下去2人。現(xiàn)在公交車(chē)上有多少人？②公交車(chē)上原來(lái)有一些人，到了一個(gè)站點(diǎn)，上來(lái)3人，下去2人。現(xiàn)在公交車(chē)上有13人，原來(lái)有多少人？通過(guò)對(duì)比兩道題學(xué)生會(huì)發(fā)現(xiàn)，第二道題可以順著思考，也可以倒過(guò)來(lái)思考，那么對(duì)比第一題哪種思考方式更好理解呢？學(xué)生通過(guò)觀(guān)察和實(shí)踐發(fā)現(xiàn)用一個(gè)未知數(shù)來(lái)表示，就可以和第一題一樣思考了，這樣建立了數(shù)量之間的相等關(guān)系，初步形成了方程思想。這時(shí)再出示③公交車(chē)上原來(lái)有12人，到了一個(gè)站點(diǎn)，上來(lái)若干人，下去2人。現(xiàn)在公交車(chē)上有13人，上車(chē)多少人？④公交車(chē)上原來(lái)有12人，到了一個(gè)站點(diǎn)，上來(lái)3人，下去若干人。現(xiàn)在公交車(chē)上有13人，下車(chē)多少人？思考怎么解答時(shí)，學(xué)生會(huì)發(fā)現(xiàn)只要抓住了數(shù)量關(guān)系，未知數(shù)可以用x來(lái)代替，這樣就可以像第一題一樣，順著思考了。通過(guò)以上題組的練習(xí)，把看似抽象的知識(shí)，讓學(xué)生借助代數(shù)思維順向找出數(shù)量之間的關(guān)系，方程知識(shí)的理解也就水到渠成。

三、 類(lèi)比推進(jìn)，讓思辨能深入

深度的學(xué)習(xí)離不開(kāi)思辨的不斷深入，只有學(xué)生圍繞知識(shí)不斷地思考，知識(shí)才能真正建構(gòu)。在題組的設(shè)計(jì)中，要重視相同類(lèi)的知識(shí)有序推進(jìn)，把多個(gè)練習(xí)在描述、情境、呈現(xiàn)方式等方面恰當(dāng)組合，通過(guò)知識(shí)間的類(lèi)比，可以幫助學(xué)生深入思考知識(shí)間的內(nèi)在聯(lián)系，將解題思路和方法由一道題拓寬到一類(lèi)題。數(shù)學(xué)題組如果能做到有序變化，學(xué)生通過(guò)強(qiáng)化舊知識(shí)，獲得新知，學(xué)生的數(shù)學(xué)思維也能不斷發(fā)展。因此教師編制題組練習(xí)要能帶領(lǐng)學(xué)生進(jìn)行認(rèn)知結(jié)構(gòu)的發(fā)展和完善，就能在清晰建構(gòu)數(shù)學(xué)知識(shí)的同時(shí)拓展思維。將有些習(xí)題進(jìn)行“變式改編”，改變題目的一些條件，讓學(xué)生可以從不同角度，不同方面接觸到知識(shí)的本質(zhì)，知識(shí)結(jié)構(gòu)在不斷重組和重構(gòu)中完善發(fā)展。用這種方式進(jìn)行教學(xué)，能使學(xué)生隨著變式的題組積極思索，找尋解決的辦法，在問(wèn)題解決中發(fā)展思維，培養(yǎng)學(xué)生思維的靈活性。

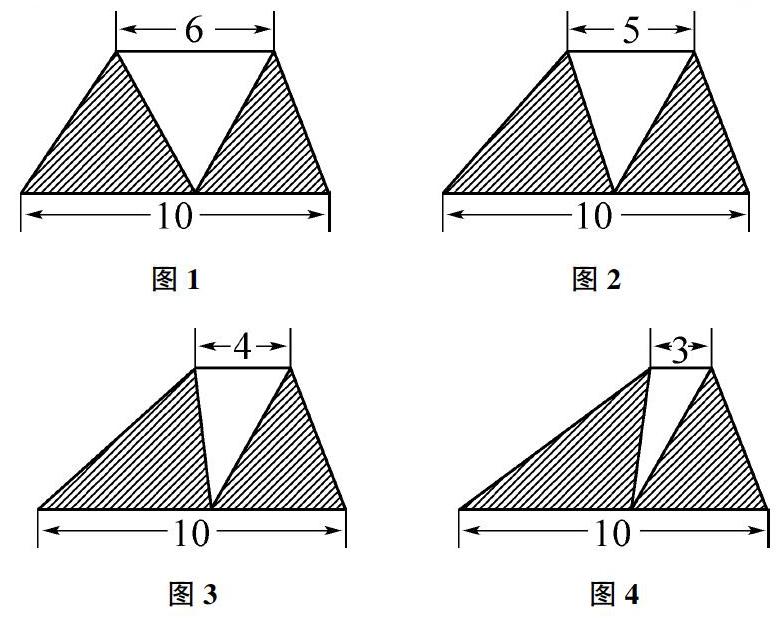
如組合圖形的面積計(jì)算是在學(xué)生掌握了平行四邊形、三角形、梯形面積之后進(jìn)行的學(xué)習(xí)的內(nèi)容。讓學(xué)生通過(guò)自主運(yùn)用已掌握的幾何知識(shí)解決不盡相同的問(wèn)題，是對(duì)學(xué)生進(jìn)行思維拓展的很好方式。組合圖形的面積計(jì)算中一方面學(xué)生要學(xué)會(huì)如何分解這些圖，另一方面學(xué)生考慮結(jié)果之間有著什么樣的聯(lián)系。在解決問(wèn)題中有樣一個(gè)圖形（圖1）：一個(gè)上底為6cm，下底為10cm，高為7cm的梯形，求陰影部分的面積。學(xué)生很快就理清了思路：梯形面積-空白三角形面積=陰影部分面積，先算梯形面積：（6+10）×7÷2=56cm2，再算空白三角形面積：6×7÷2=21cm2，最后計(jì)算陰影部分的面積：56-21=35cm2。隨后，再出示圖2、圖3和圖4，這幾個(gè)梯形的底都是10cm、高都是7cm，請(qǐng)計(jì)算這些陰影圖形的面積是多少平方厘米？

通過(guò)計(jì)算學(xué)生會(huì)發(fā)現(xiàn)這些陰影部分的面積都是35cm2，這是巧合嗎？學(xué)生通過(guò)觀(guān)察、計(jì)算、探索會(huì)發(fā)現(xiàn)陰影部分的面積和上底沒(méi)有關(guān)系只和梯形的下底和高有關(guān)系，隨著上底的不斷變小，陰影部分的面積和底是10cm高是7cm的三角形面積是相等的。

四、 網(wǎng)絡(luò)聯(lián)系，讓思維能發(fā)展

學(xué)生所學(xué)的知識(shí)如果只是一個(gè)個(gè)孤立的點(diǎn)，知識(shí)之間沒(méi)有建立起聯(lián)系的網(wǎng)絡(luò)，學(xué)生在解決問(wèn)題時(shí)就無(wú)法提取運(yùn)用相關(guān)知識(shí)。題組練習(xí)的編制要指向?qū)W生綜合知識(shí)的運(yùn)用，讓學(xué)生在題組的練習(xí)中通過(guò)對(duì)知識(shí)的不斷調(diào)用，在調(diào)用知識(shí)中不斷對(duì)比完善知識(shí)的建構(gòu)，學(xué)生綜合運(yùn)用所學(xué)的知識(shí)的能力也在辨析中不斷提高，知識(shí)點(diǎn)達(dá)到融會(huì)貫通的作用。因此老師們?cè)O(shè)計(jì)的練習(xí)要考慮整個(gè)單元知識(shí)或整個(gè)大知識(shí)體系是什么，要將題組練習(xí)的設(shè)計(jì)放在整個(gè)知識(shí)體系中來(lái)進(jìn)行，這樣才能有效提升學(xué)生的數(shù)學(xué)學(xué)習(xí)品格和關(guān)鍵能力。

百分?jǐn)?shù)作為分?jǐn)?shù)的一個(gè)下位概念，在學(xué)習(xí)時(shí)要引導(dǎo)學(xué)生將分?jǐn)?shù)和百分?jǐn)?shù)進(jìn)行對(duì)比，幫助學(xué)生更好地利用舊知有效遷移過(guò)來(lái)，在學(xué)習(xí)過(guò)程中要利用題組練習(xí)在潛移默化中培養(yǎng)學(xué)生建構(gòu)知識(shí)，和類(lèi)比推理的能力。也正是將分?jǐn)?shù)與百分?jǐn)?shù)進(jìn)行多次對(duì)比，幫助學(xué)生對(duì)兩個(gè)概念進(jìn)行區(qū)分，促進(jìn)學(xué)生對(duì)百分?jǐn)?shù)的意義和價(jià)值在題組的練習(xí)中抽象出來(lái)。如在教學(xué)中對(duì)百分?jǐn)?shù)的認(rèn)識(shí)要反復(fù)地對(duì)百分?jǐn)?shù)進(jìn)行對(duì)比，超過(guò)100%的百分?jǐn)?shù)的理解是對(duì)百分?jǐn)?shù)的一個(gè)必要理解過(guò)程。如出示出下題組：①六（1）班的男生占班全的（ ）。A. 80% B. 100% C. 200%;②冬令營(yíng)中男生占全部學(xué)生的（ ）。A. 80% B. 100% C. 200%;③書(shū)法興趣小組中男生占女生的（ ）。A. 80% B. 100% C. 200%;通過(guò)以上題組的對(duì)比，學(xué)生發(fā)現(xiàn)始終是男生與單位“1”進(jìn)行比較，但單位“1”在不斷變化，因此結(jié)果也是不盡相同的。將單位“1”的變化帶入到百分?jǐn)?shù)的理解中來(lái)，學(xué)生對(duì)百分?jǐn)?shù)的含義有了更深的理解，知識(shí)在不經(jīng)意之間建立起聯(lián)系，能夠融會(huì)貫通地運(yùn)用。

我們應(yīng)該深刻鉆研教材、理解教材的編寫(xiě)意圖。挖掘各章節(jié)的知識(shí)要點(diǎn)，通過(guò)精心設(shè)計(jì)題組，將知識(shí)點(diǎn)之間的聯(lián)系，更完整有序地呈現(xiàn)在題組模塊中。題組模塊就可以更好地將知識(shí)與學(xué)生的認(rèn)知發(fā)展規(guī)律結(jié)合起來(lái)，更好地符合數(shù)學(xué)發(fā)生發(fā)展的演繹過(guò)程。這樣才能使題組練習(xí)的功能最大化，讓學(xué)生的學(xué)習(xí)更在深度，從而提高課堂教學(xué)的效益。

參考文獻(xiàn)：

[1]黃愛(ài)華.“大問(wèn)題”教學(xué)的實(shí)施要訣[J].小學(xué)教學(xué)設(shè)計(jì)，2018（1）.

[2]周平健.讓題組練習(xí)充盈思維的張力[J].湖南教育，2012（4）.

[3]顧亞龍.題組模塊，助力課堂生長(zhǎng)[J].小學(xué)數(shù)學(xué)教師，2019（1）.

作者簡(jiǎn)介：林輝，中小學(xué)一級(jí)教師，福建省龍巖市，長(zhǎng)汀縣實(shí)驗(yàn)小學(xué)。