從錯誤中悟錯

朱明軒

【摘 ?要】 ?試卷講評是初中數學教學中必不可少的環節，對學生發現自身學習問題、矯正錯誤有積極作用。本文以學生試卷中常犯的錯誤為例，就如何引導學生從錯誤中悟錯分享自己的教學實踐經驗。

【關鍵詞】 ?初中數學;試卷講評;悟錯;糾錯

學生對知識的學習具有相對獨立性，一般通過逐個學習單個知識實現對整個知識體系的學習，然而試卷題目的解答則需要他們具備綜合運用知識的能力，二者的矛盾就催生了學生在試卷題目解答上的錯誤。試卷講評課是在考試或者試卷練習后教師對學生解題中出現的錯誤進行分析與評價的課程，通過對試卷題目的再次解答，引導學生從錯誤中悟錯，彌補學生學法上的缺陷，從而達到深化鞏固知識的目的。因此，試卷講評課的開展至關重要。

1、教學過程

筆者在實際教學實踐中發現，學生解題出現錯誤，很大程度上不是因為他們不理解、學不懂知識，而是因為他們審題不清，看題有所遺漏，混淆了概念、公式、定理的使用范圍。那么對于這類的錯誤，筆者一般采用解題過程還原的方法引導學生悟錯。以下題為例：

錯誤說明：從學生試卷反饋情況來看，個別學生該題一分沒有，主要是他們將后邊的常數項1遺漏了。

教學說明：對此，筆者邀請該題答錯的學生重新到黑板解答，并要求該生闡述自己的解題過程。在習題再次解答過程中，筆者提問該生“整式的化簡過程是怎樣的呢？”該生回答“先給分母通分，再對通分后的分子進行合并同類項，最后再化簡。”筆者追問“若所化簡的整式中有常數項，該怎么辦？”該生經過思考認識到了自己的錯誤，對整式化簡部分的知識有了更深刻的認知。之后，筆者又給出了兩道相似的題，要求學生進行解答。學生解答時，筆者巡回觀察，發現這些遺漏常數項部分的學生基本都化簡正確。

另外，學生解題出現錯誤，也有一定程度是因為他們的解題思路不清晰，考慮不全，對數學思想方法運用不當。對于這類的錯誤，筆者一般采用答案補充檢驗法引導學生從錯誤中悟錯。以下題為例：

題2：當m取何值時，二次函數y=（m2-2m-4） x+m-5的圖像在x、y軸上所截得的長度相等。

錯誤說明：這道題對大多學生來說并不難，因為整個數量關系十分明確。然而這道題答案不唯一，需要進行分類討論，從學生的試卷反饋情況來看，部分學生忽略了m=5這個答案，出現了答案不全的錯誤。

教學說明：對此，筆者針對該題提出問題“這道題的答案有幾個呢？”引發學生對該題進行再次思考，鼓勵答案不完全的學生說明自己的解題過程，并邀請答案完全的學生對其解題過程進行補充，同時，再次追問“他的答案到底對不對呢？”引導答案不完全的學生通過算式化簡、畫函數圖像對其答案進行檢驗。整個過程中，答案不完整的學生逐漸意識到了自己考慮不全的錯誤，發現了自己對字母所代表的數字含義認識上的不足。另外，筆者對于整式約分的幾種情況進行了說明。之后，要求學生自己對該題進行變式，自己出題自己做。通過課堂巡視，發現有上述錯誤的學生漸漸都開始考慮答案的完整性了。

還有，學生出現解題錯誤，也有一部分原因是他們的解題過程太復雜，導致思路混亂，從而出現錯誤。對于此類錯誤，筆者一般采用一題多解法，幫助學生找到簡潔的解題思路，以引導學生從錯誤中悟錯。以下題為例：

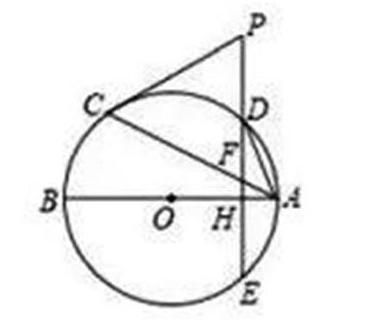
題3：如圖所示，AB、AC分別為圓的直徑和弦，點D為劣弧AC上一點，弦DE垂直于AB交圓于點E，交AB于點H，交AC于點F，P是ED延長線上的一點，且PC和PF等長。

（1）求證：PC是圓O的切線;

（2）點D在劣弧AC什么位置時，AD2=DE·DF，說明理由;

（3）在第二問的條件下，如果OH長度為1，AH長度為2，弦AC的長是多少？

錯誤說明：根據學生的試卷反饋信息，筆者發現，在第三問的解答上，好多學生用了多次的三角形相似與勾股定理，整個解題過程很復雜，有較多定理應用上的錯誤。

教學說明，對此，筆者邀請班上僅用勾股定理及圓弧的性質就將第三問解答得明明白白的學生講述自己是如何解題的。同時提出問題“還有沒有其他簡潔的解題方法？”引發學生展開討論，基于此開展一題多解教學，并滲透相關知識定理的正確運用，引導學生發現自己解題中的錯誤，感受相同題目的多種解題方法。

2、教學反思

數學試卷講評課的對象是數學題目，然而其目的不在于將題目講得多深、多透，而在于引導學生主動發現錯誤，從錯誤中悟錯，同時給他們提供糾正錯誤的機會。教師存在的價值就是引發學生的思考，而不是讓學生對自己、對教材產生依賴。一旦學生對教師、對教材有較強的依賴性，那么他們的思維能力就會退化，更不必說是運用綜合性思維解決復雜問題了。通過對學生解題錯誤的分析，我們可知，不理解知識并非他們出現錯誤的真正原因，實際原因在于審題不清、不會靈活解題。對此，教師就需要根據學生的錯誤原因、錯題性質，采取針對性的教學方法，以加強學生對正確、簡潔的解題方法的學習。另外，數學題目中，有很多都是需要用到概念進行解答的。因此，教師也不能忽略概念的應用題目講評。

【參考文獻】

[1]劉穎婕.淺談初中數學試卷講評課的有效性[J].中學數學教學參考，2016（21）：16-17.

[2]陳艷秋.初中數學試卷講評探究——以蘇教版初中數學為例[J].數學教學通訊，2018（08）：40-41+67.