斜齒面齒輪齒面接觸問題的有限元-線性規劃解法
宋相男,靳廣虎
(南京航空航天大學 直升機傳動技術實驗室, 江蘇 南京 210016)
0 引言
本質上而言,面齒輪傳動是漸開線圓柱齒輪與錐齒輪相嚙合的齒輪傳動[1],在直升機主減速器的傳動系統、銑床主軸的傳動系統以及自行車的無鏈條傳動系統中均有很好的應用。其特有的結構和嚙合特性使其具備諸多優勢,成為21世紀直升機傳動系統研究的重點。
LITVIN.F.L研究了面齒輪齒面成形的理論方法及齒面接觸應力的分析[2-3];沈云波等分析了斜齒面齒輪齒寬限制條件[4-5];方宗德、WU S H及YE.S.Y等人基于齒輪齒面的柔度矩陣對齒面接觸應力進行了計算[6-9];T.F.Conry等基于線性規劃的思想提出了彈性接觸問題的解法[10-12];唐進元基于有限元的思想計算了螺旋錐齒輪的嚙合剛度[13]。
本文提出基于有限元-線性規劃法對斜齒面齒輪齒面接觸問題進行計算的方法,基于齒面接觸區域的載荷和變形量計算了齒輪副的嚙合剛度及最大壓應力。
1 斜齒面齒輪的齒面成形及接觸軌跡
1.1 齒面數學模型
斜齒面齒輪齒面十分復雜,無法直接將其齒面方程表示出來,需借助其加工刀具齒面方程,并結合齒輪嚙合方程間接對其齒面加以描述。
1) 插齒加工坐標系
根據斜齒面齒輪插齒加工原理,建立如圖1所示加工坐標系。其中,ssc(o-xsc,ysc,zsc)為刀具的固定坐標系,ss(o-xs,ys,zs)是與刀具固聯的轉動坐標系,sfc(o-xfc,yfc,zfc)為面齒輪的固定坐標系,sf(o-xf,yf,zf)是與面齒輪固聯的轉動坐標系,φs和φf分別為刀具與面齒輪的轉角。
2) 刀具的齒面方程
圖2為刀具端面齒廓及坐標系,該坐標系與圖1中的坐標系對應。其中,θs為刀具漸開線齒廓上的角度參數;θsc為刀具基圓上齒槽寬所對應圓心角之半,其計算公式為
θsc=2π/Ns-(tanαst-αst)
(1)
式中:Ns為刀具齒輪的齒數;αst表示刀具端面壓力角。
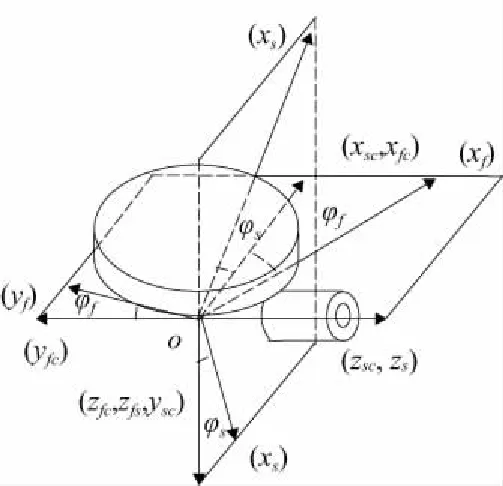
圖1 斜齒面齒輪插齒加工坐標系

圖2 刀具齒面坐標系
漸開線齒廓方程為:
(2)
式中:rbs為刀具基圓半徑;“±”分別表示漸開線齒廓Ⅰ和Ⅱ。
漸開線斜齒輪刀具的齒面由端面齒廓沿z軸作螺旋運動掃略形成,故刀具齒面1(即齒廓Ⅰ螺旋而成的齒面)方程表示為:
(3)
同理,齒面2方程為:
(4)
式中:γs為端面齒廓沿z軸螺旋的角度;ps為螺旋參數,其計算公式為
ps=2πrbs/tanβb
(5)
式中βb為刀具基圓螺旋角。
3) 斜齒面齒輪的齒面方程
根據包絡理論和齒輪嚙合原理,則得斜齒面齒輪的齒面方程為:
(6)
式中:Mf,s是坐標系ss到sf的坐標轉換矩陣;f(θs,γs,φs)是齒面嚙合方程。Mf,s表示為:
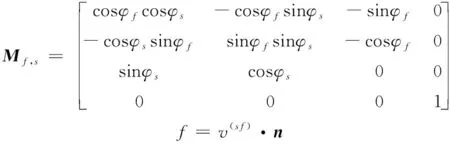
其中:v(s, f)為刀具與面齒輪嚙合點處的相對運動速度;n表示嚙合點處法向量。
1.2 齒面嚙合軌跡
采用齒數N1比刀具齒數Ns少1~3個,且其他參數與刀具一致的漸開線斜齒圓柱齒輪與面齒輪嚙合,實現點接觸傳動。因齒面參數相同,故斜齒輪齒面方程與刀具相類似,其齒面方程用r1(θ1,γ1)表示。
嚙合傳動時,兩輪齒面連續相切,則在固定坐標系中,兩輪齒面接觸點具有相同的坐標和法向量,即:
(7)

依據上述理論分析,利用matlab編寫程序,實現斜齒面齒輪齒面及接觸軌跡的可視化,如圖3。
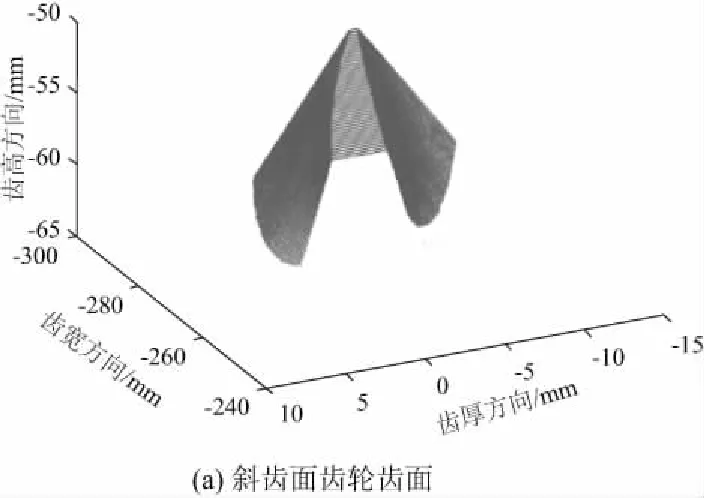
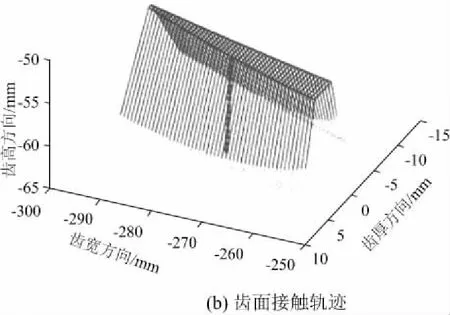
圖3 斜齒面齒輪齒面及接觸軌跡
2 斜齒面齒輪齒面接觸問題計算理論
2.1 面齒輪彈性接觸問題的基本理論
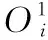
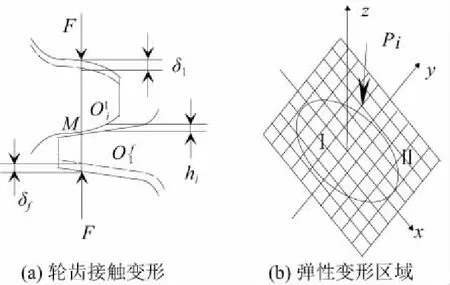
圖4 斜齒面齒輪接觸情況
取區域Ⅱ包含實際接觸區域Ⅰ,區域Ⅱ上各點的彈性力為Pi,區域Ⅱ上點是否在實際接觸區域Ⅰ上的判別條件為:
1) 在接觸區域Ⅰ:
(8)
2) 不在接觸區域Ⅰ:
(9)
式中:δ為兩輪齒的整體接近量,δ=δ1+δf。
各點的接觸彈性變形可表示為:
ωi=ai·pi
(10)
式中ai表示各點的齒面柔度系數。
設區域Ⅱ上共有N個節點,則各點彈性力之和為F,即
(11)
由式(8)-式(11)可得到區域Ⅱ上各節點的初始距離hi、節點力pi、彈性變形ωi和輪齒的整體接近量δ滿足:
(12)
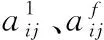
記區域Ⅱ上斜齒輪和面齒輪齒面上各節點的柔度系數之和為一N×N階矩陣A
(13)
則式(12)可改寫為:
(14)
式中:P=[P1,P2,…,Pn]T,H=[h1,h2,…,hn]T為N×1階列向量。
2.2 兩齒面對應節點間初始距離hi的求解


(15)
式中:t為坐標參數,其值為任意實數。

(16)
3 齒面載荷分布的線性規劃算法
3.1 面齒輪彈性接觸問題的數學模型
將變形協調條件式(8)和式(9)改寫為
(17)
引入松弛變量Yi(Yi≥0),則上式可寫為
(18)
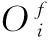
(19)
將式(18)代入式(14)可獲得斜齒面齒輪齒面彈性接觸問題的數學模型:
(20)
式中:{e}為N×1階單位向量;[I]為N×N階單位矩陣;P=[P1,P2,…,Pn]T、H=[h1,h2,…,hn]T為N×1階列向量。
該模型中需求解的未知量為(P,δ,Y),Pi≥0,δ≥0,Yi≥0,且各未知量均需滿足接觸條件式(19)。
3.2 改進的單純形法計算齒面載荷
參照線性規劃的一般形式,將斜齒面齒輪的彈性接觸問題改寫為:
在約束條件:
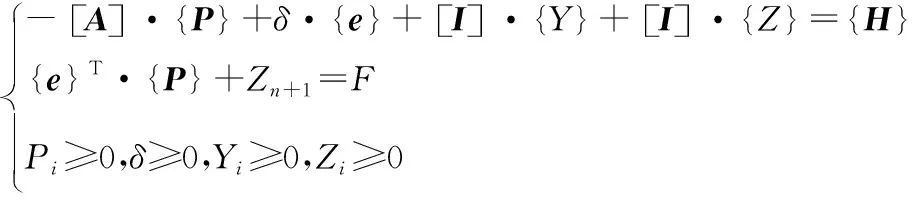
(21)
下,求目標函數
(22)
的最小值。
式中:Zi為人工變量,其值非負。
該問題不同于一般線性規劃問題之處在于其附加有接觸條件式(19),將該問題表示如表1所示。

表1 面齒輪彈性接觸問題的線性規劃表示
表1第一行元素為待求的各未知量,往后每行代表一個約束條件,共有N+2個約束條件,最右邊一列的值為等式約束式(21)的右邊常數項。
將表1的第N+2約束行元素減去前N+1約束行元素之和,并將結果放置于原第N+2約束行,獲得改進后的形式如表2所示。

表2 面齒輪彈性接觸問題的改進線性規劃表示
表2中,di、Zd可分別表示為:
(23)
由表2可知,Zi的系數矩陣為一單位陣,故令Zi為基變量,令(P,δ,Y)為非基變量,取值為0,得初始基本可行解。因未知量數遠大于方程數,故有多組基本可行解,但僅有一組為所需解。由線性規劃的求解過程可知,得到一組基本可行解后,需不停地進行轉軸運算,使各變量不斷進入或退出基變量,找出一組使目標函數取最小值的可行解。
任何一個非基變量xs增加一正增量Δxs,將使目標函數變化為Zd+dsΔxs,為使目標函數減小最快,應使ds為di中的最小負值。找出變量xs所在列的所有正系數ais,其對應最右邊的常數項為bi,作比值bi/ais,找出所有比值的最小者。假設在r行,則以r行s列元素為轉軸元素進行轉軸運算。此時,原非基變量xs進入基本可行解,而相應的Zr則退出基本可行解。
用該方法求解斜齒面齒輪的齒面接觸問題時,有附加接觸條件式(19),故對進入基本可行解的變量有限制條件。假設某次進入基本可行解的變量選為Ps,則需檢查與之對應的Ys是否為基變量。若否,Ps可自由進入基本可行解;若是,Ps進入后Ys退出,則此次Ps仍可進入,否則找出di中除ds以外的最小負值所在列的變量進入基本可行解;同理,若某次進入基本可行解的變量選為Ys,則應對相應的Ps進行檢查。
重復上述運算過程,直至得到滿足接觸條件的基本可行解。實際計算表明,在2×(N+1)個循環內便可以得到唯一可行解。
3.3 齒輪副綜合嚙合剛度的求解
斜齒面齒輪的齒厚在齒寬方向上不斷變化,故目前還未見斜齒面齒輪副嚙合剛度的解析求解法。基于以上求解,可獲得接觸區域上各節點的載荷和變形,從而求得單對齒嚙合剛度:
(24)
式中δu為單對輪齒的綜合彈性變形。
本文中,δu定義為整片接觸區域上所有對應節點間彈性變形的平均值,即
(25)
式中m為實際接觸的節點個數。
多對齒接觸時,各接觸齒對間可看作是并聯彈簧,故將同時嚙合輪齒的單對齒嚙合剛度進行分段疊加,即可得嚙合副的綜合嚙合剛度Km:
(26)
式中s為同時嚙合的輪齒對數。
3.4 實例計算
斜齒輪的法面模數mn=4,齒數N1=27,壓力角α=22.5°,螺旋角β=10°,刀具齒數Ns=28,面齒輪齒數Nf=131。
1) 初始距離hi
圖5所示為接觸點附近兩齒面對應點間的初始距離圖。由圖可知,斜齒面齒輪內徑靠近齒根和外徑靠近齒頂處,兩齒面上對應點間的初始距離較大,而在接觸點附近,兩齒面上對應點間初始距離較小,該趨勢與兩齒面形狀吻合。
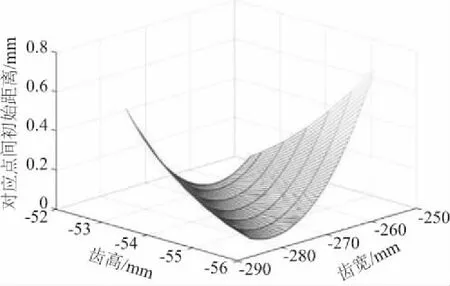
圖5 接觸區域對應點間初始距離
2) 接觸區域載荷分布
圖6所示為斜齒面齒輪齒面接觸區域上的載荷分布,該接觸區域上最大載荷出現在初始接觸點(橢圓中心)處,接觸區域的載荷在空間內呈半橢球體分布,這與Hertz接觸理論是吻合的。

圖6 接觸變形區域載荷分布
3) 嚙合剛度
根據式(22)和式(23)求得單對齒從嚙入到嚙出過程中,嚙合剛度計算值及傅里葉擬合曲線如圖7。
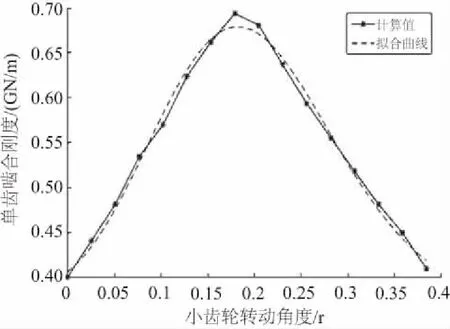
圖7 單齒嚙合剛度曲線
將單對齒嚙合剛度曲線向左、右移動角度Δφ可得臨近齒對的單齒嚙合剛度曲線如圖8。Δφ為斜齒圓柱齒輪轉過一個周期的轉角與重合度的比值。

圖8 各嚙合齒對的嚙合剛度
將各單齒對的嚙合剛度按式(24)進行分段疊加,得綜合嚙合剛度,如圖9。
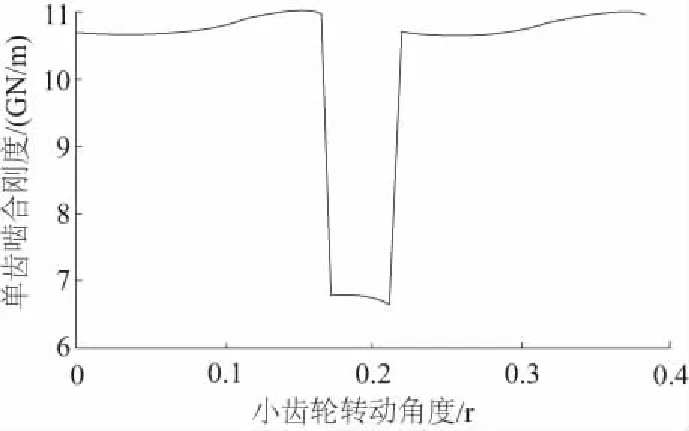
圖9 綜合嚙合剛度
4) 最大接觸應力計算結果與驗證
采用本文方法和Hertz理論法分別計算單對齒嚙合時接觸區域的最大接觸應力,結果如圖10所示。其中,施加的載荷F=2500N。由圖可知,嚙合過程中,兩種方法所得接觸應力的最大誤差為7.87%,最小誤差接近0。

圖10 斜齒面齒輪齒面最大接觸應力
4 結語
本文主要做了如下工作:
1)通過包絡理論和齒輪嚙合原理推導了斜齒面齒輪的齒面方程,并基于matlab實現其齒面及接觸軌跡的可視化。
2)建立適合斜齒面齒輪接觸問題的線性規劃模型,對單純形算法加以改進,求得齒面載荷分布和各接觸位置的彈性變形,給出了基于有限元和線性規劃求解斜齒面齒輪副嚙合剛度的方法。
3) 通過與傳統的Hertz接觸理論計算出的接觸應力進行對比,得到的誤差均在8%以內,證明了本文方法的有效性。
本文為斜齒面齒輪齒面接觸問題提出了一種行之有效的計算方法,給出了一種計算斜齒面齒輪副嚙合剛度的途徑,為斜齒面齒輪傳動中接觸強度的分析提供了一定的理論基礎。

