基于掌握學習理論下的微課輔助教學實踐*

廣東省廣州市聚德中學()

平時的數學教學中，數學老師總有這樣的苦惱，題目講過了好多次了，學生怎么還會錯呢? 雖然知道多講幾次會提高答對率，但是，教學進度緊、教學時間往往不允許.學生總會有這樣的煩惱：明明上課聽懂了，再次遇見類似的題目，怎么還是做不出呢? 針對這兩點，筆者用一道特殊四邊形背景下的將軍飲馬問題，在一個班級進行測試，試圖回答3個問題：(1)學生要講幾次才能達到90%的準確率? (2) 微課要如何嵌入更有效? (3)將軍飲馬問題的最大難點是什么?

1 測試班級學情

測試班級的總體情況：八年級，人數：47.學生總體情況：八年級上冊期末測試，該班平均分在海珠區排名第5.

2 測試過程

2.1 初次遇見，11人給出正確答案

如圖1所示，正方形ABCD的面積為12，ΔABE是等邊三角形，點E在正方形ABCD內，在對角線AC上有一點P，使PD+PE的和最小，則這個最小值為( )

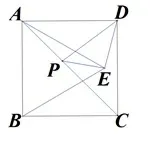
圖1

本道題是八年級下學期學完平行四邊形，某份復習卷的第10題(選擇題最后一道)該題考察的是正方形背景下的將軍飲馬問題：線段之和的最小值.學生要在較多線干擾的情況下識別將軍飲馬問題，要找到點P，能由正方形面積求出邊長.關鍵點：知道為什么點P是BE與AC的交點，BE的長度就是所求的PD+PE最小值.

2.2 同學交流，換個背景

小測題目：如圖2，菱形OBCD，B(5,0),M(0,1)，K是OC上一點，求DK+MK的最小值.

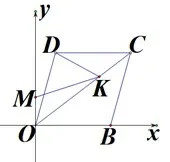
圖2

這次測試是在第二天，上述題目沒評講，只是學生之間有交流過，19個學生結果對，其中，14個學生的圖沒畫完整，無法判斷是否真會.該題與試卷上的題……