精選素材，巧求15°角的三角函數(shù)值

廣東省佛山市順德區(qū)順德德勝學(xué)校

特殊角的三角函數(shù)值，是我們比較喜歡在圖形中研究和用來考查同學(xué)們應(yīng)用知識能力的一個重要知識點.筆者在教學(xué)中，結(jié)合對北師大九年級(下)27頁的復(fù)習(xí)題第22題的研究和思考，引導(dǎo)學(xué)生思考探討：應(yīng)用銳角三角函數(shù)定義求15°角的三角函數(shù)值問題.

原題如下：

把一條長1.35m的鐵絲彎成頂角為150°的等腰三角形，求此三角形的各邊長(結(jié)果精確到0.01m).

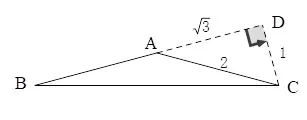
圖1

筆者在挖掘教學(xué)素材時，總想改編為讓學(xué)生不用精確到0.01，而直接保留根號的計算結(jié)果.于是結(jié)合圖形，引導(dǎo)學(xué)生通過構(gòu)造含30°角的直角三角形加以解決，其關(guān)鍵就是解決15°角的三角函數(shù)值的問題.

解如圖1，在ΔABC中.因為AB=AC,∠BAC=150°，所以∠B=∠ACB=15°.過C作CD ⊥AB交BA的延長線于點D,則在RtΔACD中，∠CAD=30°.設(shè)CD=1,則AC=2,AD=所以AB=AC=2.BD=AB+AD=2+√所以在RtΔCBD中，tan ∠CBD =即但當(dāng)要求sin 15°,cos 15°時，需要BC的長度，這時根據(jù)勾股定理可得所以

到此，對BC的進(jìn)一步化簡技巧，成了絕大部分同學(xué)的難以逾越的障礙.由此，大部分同學(xué)對sin 15°,cos 15°的函數(shù)值望而卻步.

對這個問題的探討，人教版的九年級(下)教師教學(xué)用書(2014年10月第1版，2017年9月第5次印刷)在167頁的拓展性問題也進(jìn)行了相關(guān)研討，原文如下：

1.不查表，你能求15°的三角函數(shù)值嗎？

【答案與提示】構(gòu)造一個有一個銳角為15°的直角三角形，再利用銳角三角函數(shù)的定義求解.

解如圖2，作ΔABC,使AB=AC,且∠BAC=30°,過點A作AD ⊥ BC于點D,過點C作CE ⊥ AB于點E.

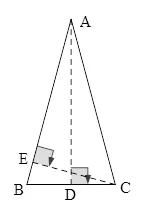
圖2

不妨設(shè)AB=AC=2a，則CE=a,AE=所以

在RtΔBCE中，由銳角三角函數(shù)定義，得sin 15°=

教師用書中同樣涉及到的化簡運(yùn)算技巧問題.

這時，我們自然會想到，當(dāng)一副三角板疊放在一起時，也有15°的角，能否用平常用的三角板，構(gòu)造出適當(dāng)?shù)膱D形，解決上述問題？……