正方形中的那些事*

廣東省深圳實驗學校初中部()

1 正方形中的垂直結構

例1 如圖1，已知正方形ABCD中，點E,F,G,H分別在邊AB,CD,AD,BC上，若EF ⊥ GH，判 斷EF與GH的數量關系.

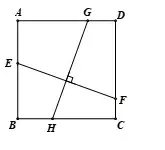
圖1

教學片段

教師：正方形給我們的第一印象是“方正”，這種感覺是由正方形中的“垂直結構”所保證的.正方形的對角線不僅有“互相垂直”的位置關系，還有“相等”的數量關系，那么對于一般的垂直結構，有類似的結論嗎?

圖2

生1：可以過點G作GM ⊥BC，過點F作FN ⊥ AB，證明ΔGMH∽= ΔFNE.(圖2)

教師：很好，還有別的證法嗎？

生2：還可以過點D作DP//GH，過點C作CQ//FE，證明ΔDCP=∽ ΔCBQ.(圖3)

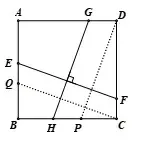
圖3

教師：通過“作垂直”或“作平行”的方法，構造全等三角形，得到結論：兩條互相垂直的直線被正方形對邊截得的線段長相等.

例2如圖4，將邊長為12的正方形ABCD折疊，使得B點落在邊AD上的P點，若折痕_EF的長為13，求線段PD的長.

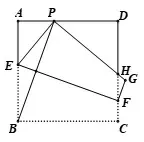
圖4

解析識別折疊問題中的垂直結構：PB ⊥EF，得到PB=EF=13,則AP=5,故PD=7.

圖5

方法提煉還可以將正方形中的垂直結構推廣到矩形(圖5)中，由ΔGMH∽ΔFNE，得：

2 正方形中的45°

例3如圖6，正方形ABCD邊長為2，點E,F,G,H分別是在邊AB,CD,AD,BC上，且EF與GH的夾角為45°，若EF=求GH的長.

圖6

教學片段

教師：除了90°角，正方形常常還與45°角相結合，如：對角線平分一組對角、半角模型等.

生3：仿照例1的作法，將線段EF和GH平移到點B處(即過點B作BM//EF,BN//HG)，則：∠MBN=45°,可構造半角模型.(圖7)

圖7

例4(例2 變式)如圖4，將邊長為12的正方形ABCD折疊，使得B點落在邊AD上的P點.

教學片段

教師：我們回到前面的折疊問題，在這個例題中，存在45°角嗎？提出你的猜想.

生4：連接BH,猜想：∠PBH=45°.(圖8)

圖8

教師：如何證明呢？小組成員互相討論.

生5：小組討論得：先證PB平分∠APH,再作BM ⊥PH,證明：ΔBAP∽= ΔBMP,ΔBCH∽= ΔBMH.

解析因為∠EPB=∠EBP,AD//BC.所以∠BPH=∠PBC=∠APB.易證：ΔBAP∽= ΔBMP(AAS)，ΔBCH∽= ΔBMH(HL).所以45°.

教師：除了∠PBH為定值外，題目中還有“變化中的不變量”嗎？……