一類不等式(等式)證明問題的降格處理

形如a1+a2+···+an ≥(=,≤)f(n)、a1a2·····an≥(=,≤)g(n)的數列前n項和、積型不等式、等式的證明問題，在高考及競賽試題中時有出現.此類問題涉及函數、數列、不等式等高中數學的核心內容，是高考及競賽的一個熱點和難點.解決此類問題的通常方法是放縮法、數學歸納法和利用數列單調性等，方法較難較繁，對考生的能力有較高的要求.若從數列的觀點看，上述兩式的左邊分別是數列{an}的前n項和、積，若把f(n),g(n)分別視為數列{bn}的前n項和、積，(若f(n)=c(非零常數)，可把c視為無窮等比數列{bn}的前n項和Bn的極限即所有項和B)，則問題的實質是兩個數列{an}與{bn}的前n項和或積的不等或相等問題，從而只要通過比較數列{an},{bn}的通項an,bn的大小即可.這樣就把證明兩個數列前n項和、積的不等、相等關系降格為證明相應通項的不等、相等關系，從而可使問題化難為易，化繁為簡.茲舉例說明.

1.把證明兩數列前n 項和、積的相等關系降格為證明相應通項的相等關系

例1(《數學》選修2-2(湖南版)第140 頁第9(3)題)證明：

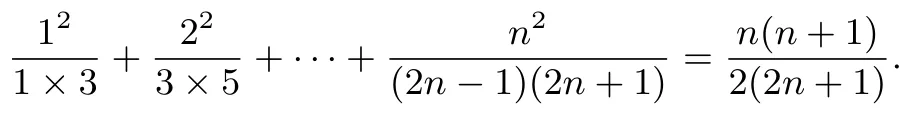
簡析記原式左右兩邊分別為數列{an},{bn}的前n項 和An,Bn，則bn=Bn -2)，并且也適合上式，則bn=(為節省篇幅，以下各例將略去這一步).于是有an=bn(n ∈??，從而可得An=Bn，即原式成立.

例2(ⅠMO-8試題)對于一切正整數n及每個實數(k= 0,1,··· ,n,m是任意整數)，求證：

簡析記原式左右兩邊分別為數列{an},{bn}的前n項和An,Bn，則

且b1=B1= cotx-cot 2x=也適合上式.則有an=bn(n ∈??),從而可得An=Bn，即原式成立.

例3證明cosxcos 2x·····cos 2n-1

簡析記原式左右兩邊分別為數列{an},{bn}的前n項乘積An,Bn，則an=cos 2n-1x，

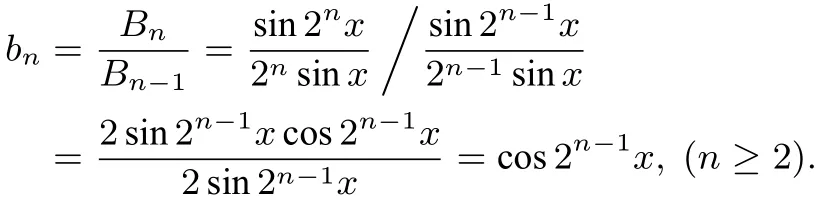
且易求得b1=B1= cosx也適合上式.則有an=bn(n ∈??)，從而得An=Bn，即原式成立.

例4(2018年高考天津卷理科第18 題)設數列{an}是等比數列，公比……