一道清華大學自招試題的解法探究及拓展
2020-02-20 07:50:50廣東省中山市濠頭中學528437
中學數學研究(廣東)
2020年1期
關鍵詞:解題
廣東省中山市濠頭中學(528437) 閆 偉
1.試題呈現與分析
例1(2019年清華大學自主招生考試第8 題)已知橢圓,過點F(2,0)的直線與橢圓交于A,B兩點,點C在直線x= 3 上,若?ABC為等邊三角形,求?ABC的面積.
試題分析題目結構清晰,以橢圓為背景,主要考查橢圓的焦點弦、幾何性質、直線與橢圓的位置關系,三角形的面積等知識以及轉化與化歸、數形結合等數學思想,突出考查學生邏輯推理、推理論證及運算求解等方面的能力,試題的思維過程和運算過程體現了能力立意的命題思想,較好地體現了對直線與圓錐曲線的核心內容和基本思想方法的考查,亦較好地檢測學生的數學素養和學習潛能.
2.解法探究
解法1(通性通法,少思多算)設直線l:x=my+ 2,A(x1,y1),B(x2,y2),AB中點為N,聯立整理可得(m2+3)y2+4my-2=0,
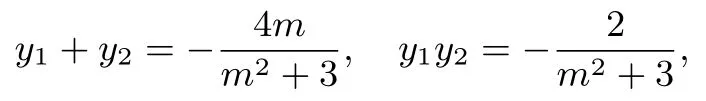
易求得N點橫坐標

因為?ABC為等邊三角形,所以CN ⊥AB,即kCN=-m,于是
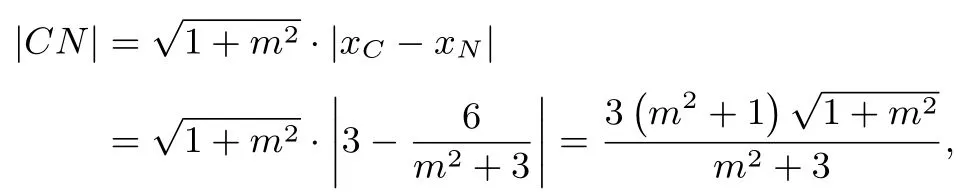
評注本解法通過設直線方程并聯立直線與橢圓結合韋達定理,再利用坐標表示弦長建立關于斜率的等式達到求解參數的目的,解題思路清晰,學生容易想到,但是運算較為繁瑣,要求學生提高數學運算能力.下面先給出兩個結論:
(1)設AB是過橢圓= 1 (a > b >0)右焦點F的弦,直線AB與x正半軸所成的角為θ,則
(2)設橢圓焦點弦AB的中垂線交長軸于點D,則e為橢圓的離心率.

圖1
證明(1)如圖1所示: 過A點作直線的垂線于A1,由橢圓的第二定義知即化簡整理得同理得
(2)如圖1知

解法2(巧用結論,多思少算)設直線AB與x正半軸所成的角為θ,由題意知離心率根據上述結論正三角形的邊長|AB|=過A,B分別作直線x= 3的垂線,垂……
登錄APP查看全文
猜你喜歡
小學生學習指導(低年級)(2022年9期)2022-10-08 03:12:02
小學生學習指導(低年級)(2021年4期)2021-07-21 01:59:26
中學數學雜志(2019年1期)2019-04-03 00:35:46
數理化解題研究(2017年4期)2017-05-04 04:07:56
讀寫算(下)(2016年11期)2016-05-04 03:44:22
中學生數理化·八年級數學人教版(2016年3期)2016-04-13 09:17:06
中學生數理化(高中版.高二數學)(2016年10期)2016-03-01 03:46:37
讀寫算(下)(2016年9期)2016-02-27 08:46:44
讀寫算(下)(2015年11期)2015-11-07 07:20:59

