2019年高考全國Ⅱ卷解析幾何試題的探究與推廣*

北京市第十二中學(100071) 劉 剛

1.試題

真題(2019年高考全國Ⅱ卷理科第21 題)已知點A(-2,0)、B(2,0)，動點M(x,y)滿足直線AM與BM的斜率乘積為記M軌跡為曲線C.

(1)求C的方程，并說明C是什么曲線？

(2)過坐標原點的直線交C于P、Q兩點，點P在第一象限，PE⊥x軸，垂足為E，連接QE并延長交C于點G.(i)證明： ?PQG是直角三角形;(ii)求?PQG面積的最大值.

試題考查了曲線的方程、直線和橢圓的位置問題以及最值問題，考查了學生分析問題與解決問題的能力，體現了邏輯推理、直觀想象、數學運算等數學核心素養.試題解法靈活，內涵豐富，綜合性強，為不同學生搭建了施展才能的舞臺，是一道好題.

2.解法探究

解答(1)C的方程是C是中心在坐標原點，焦點在x軸上的橢圓，不含左、右頂點，過程從略.

(2)解法1 (i)設直線PQ的斜率為k，則其方程為y=kx(k ＞0)，與C的方程聯立，解得則P(u,uk)，Q(-u,-uk),E(u,0)，于 是直線QG的斜率為方程為將其與C的方程聯立，得

設G(x0,y0)，則-u和x0是方程①的解，所以x0=由此得從而直線PG的斜率為

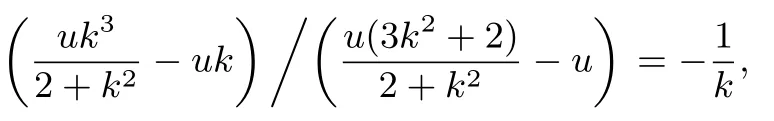
所以PQ⊥PG，故?PQG是直角三角形.

(ii)由(i)得所以?PQG的面積

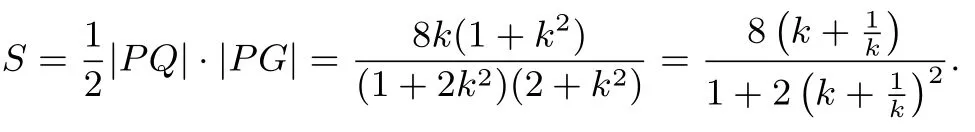
點評解法1 第(i)問以直線PQ的斜率k為研究對象，先聯立直線PQ與C的方程，并為了表達簡便，設出進而得到點P,Q,E的坐標，在此基礎上求出直線QG的方程并與C的方程聯立，然后運用韋達定理得到點G的坐標，最后借助斜率完成解答，體現了坐標法的應用;第(ii)問在第(i)問的基礎上先表示出?PQG的面積，然后化簡、換元，最后借助函數的單調性求得最值，體現了解析幾何與不等式、函數交匯的特點.

解法2 (i)設由已知得E(2 cosα,0)，所以

因 為Q,E,G三點共線，所以共線，即整理得2 cosαsinβ-sinαcosβ+cosαsinα=0，于是cosα(sinα+sinβ)=sin(α-β)，即

由此得

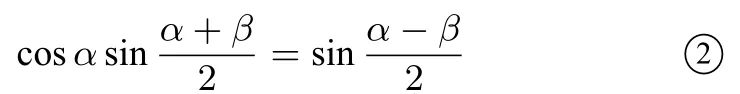
因 為所以……