大學生近年來公共數學成績分析

齊暢 章葉璐 晏建學

摘 要：學生成績是衡量學生對課程的掌握情況及教師的教學效果最直接的指標，傳統的成績分析方法是按分數段劃分并根據正態分布計算平均成績和方差。本文主要從正態分布模型檢驗及聚類分析兩方面入手，利用SPSS軟件對財經大學2010學年至2017學年部分班級公共數學成績進行分析，更科學、合理地反映學生對課程的掌握情況，并檢驗教師的教學效果。

關鍵詞：正態模型檢驗 聚類分析 SPSS

基金項目：本文為“第十三屆云南財經大學本科生科研訓練計劃（SRTP）（項目編號47《云南財經大學近年來公共數學成績聚類分析》）”項目成果。

本文以2010～2017級部分授課班級成績為例，數據包括學號、姓名、班級編號、課程名稱、教學老師、年級、學生總成績等。數據情況如下：

首先檢驗學生成績是否服從正態分布，然后用聚類分析功能對學生成績進行分析，并檢驗不同班級、年級、教師之間學生成績分布差異是否明顯，同一老師所帶不同班級、不同年級學生成績差異是否明顯，不同老師不同學院不同班級學生成績差異是否明顯，不同年級之間學生成績差異是否明顯。用聚類分析彌補傳統按分數段劃分及根據正態分布計算平均成績和方差的不足，更加科學、合理地反映學生對課程的掌握情況及教師的教學成果。

1 對數據分課程進行正態分布模型檢驗

將2010～2017級的概率論與數理統計（理工類）、微積分（經管類）、微積分（理工類）、線性代數（經管類）、線性代數（理工類）這五門不同的公共數學課程作為分類的依據。

分別對上述課程的學生成績進行正態分布模型檢驗。按照“分析-描述統計-探索”的步驟進行操作，將“成績”作為因變量，得到輸出結果（詳見附錄）。對數據的正態性進行擬合優度檢驗，首先進行“數據-加權個案”操作，再由“分析-非參數檢驗-卡方”進行操作，將“成績”作為因變量，得到輸出結果（詳見附錄）。

從輸出結果中，可以看到各個課程的成績都沒有均勻地分布在某個特定的區間內，而是存在有很多偏離區域很大的點。同時，可以看到各個課程的成績漸進顯著性均為0，而卡方擬合優度檢驗中，該項值小于0.05即視為不滿足預期頻數，因此可以得出：成績沒有服從正態分布。

2 采用K-Means聚類對成績分課程進行聚類分析

經過多次嘗試，最終確定聚類數目為3類，以下進描述聚類數目為的聚類結果。

將上述不同課程的學成成績進行聚類分析。按照“分析-分類-聚類”步驟操作，將“成績”作為變量，并將聚類數設置3，勾選“保存”中的“聚類成員”“與聚類中心的距離”項目和“選項”中的“每個個案的聚類信息”項目，得到輸出結果。

從輸出結果中以“概率論與數理統計（理工類）學生成績聚類分析結果”為例可以看到，三個類的聚類中心點，分別是29、63、80。最終聚類中心間的距離，第一類與第二類的距離為34.527，第一類和第三類之間的距離為51.458，第二類和第三類之間的距離為16.931。

從輸出結果還可以看出，在以63為聚類中心點的第二類數據樣本數是最多的，而以80為聚類中心點的第三類數據樣本數次之，以29為聚類中心點的第一類數據樣本數最少。

縱觀另外四組輸出結果，除了微積分（理工類）和線性代數（經管類）之外，微積分（經管類）和線性代數（理工類）均符合這樣的規律。因此我們將對數據進行分課程、年級、老師進行聚類分析，以期得到一個普適的規律。

3 采用K-Means聚類對成績分課程、年級、老師進行聚類

通過2010～2017年公共數學學生成績，進行分課程、老師、年級，再對每組數據進行聚類分析。具體操作步驟如上所述，得到輸出結果：當以課程、年級、老師作為分類的依據，對學生成績以3個類進行聚類時，基本上剛好可以劃分為不及格，剛及格，高分這三個類別。其中，不及格的聚點在8～56之間，其中33為眾數。及格的聚點在60～73之間，其中62、64為眾數。高分的聚點在75～87之間，其中77為眾數。自2010年起到2017年的八年中，不及格的學生成績雖有略微提高，但是變化不大。及格的學生成績則變化較大，提升了6～7分。高分組的學生成績比較穩定，上下浮動不大。同時從輸出結果中可以看到教師的不同對學生成績的分布并無太大影響。

4 采用K-Means聚類對成績分課程、老師進行聚類

由于考慮到不同老師的教學方法的不同，將所采集到的數據分老師、課程再次進行聚類分析。具體操作步驟如上所述，得到輸出結果如下：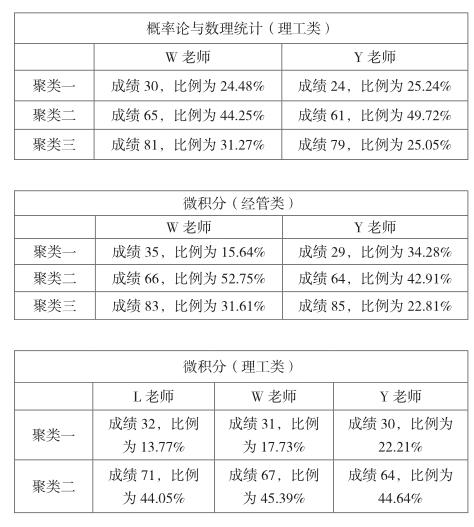

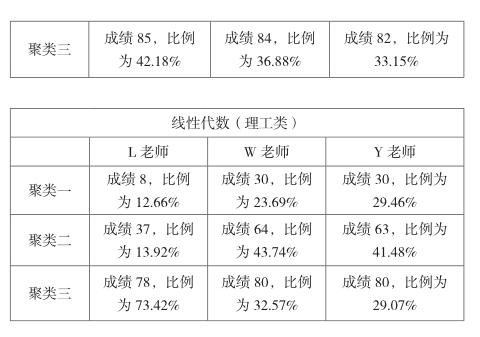
通過對不同老師相同課程的橫向比較發現：每位老師的各個課程的橫向比較，學生成績的劃分大致相同，且所占比例最多的聚類中心點在成績65左右。

5 對數據分課程得出的聚類進行正態分布模型檢驗

從正態分布模型中看出雖然整體并不服從正態分布，現探究是否存在某一定區域內的數據服從正態分布。

將2010～2017級的概率論與數理統計（理工類）、微積分（經管類）、微積分（理工類）、線性代數（理工類）這四門不同的公共數學課程對按3類聚類進行聚類分析輸出的結果再次根據各自的聚類再次進行正態分布模型檢驗。

從輸出結果中，可以看到各個課程的每個聚類成績都是均勻地分布在某個特定的區間內，并沒有存在有很多偏離區域很大的點。同時，可以看到各個課程的成績漸進顯著性，該項值均大于0.05，即視為滿足預期頻數。

因此可以得出結論：各個課程聚類分析后每個聚類成績各自服從正態分布。

6 對各個課程聚類分析后每個聚類各自再次進行K-Means聚類

經過多次的嘗試，最終確定聚類數目仍為3類。

具體操作步驟如上所述，得到的輸出結果如下所示：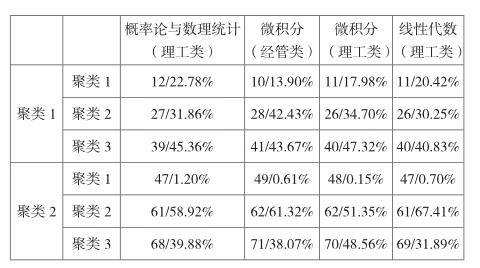

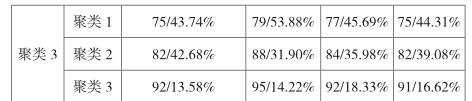
從輸出結果來看，通過將各個課程的聚類分析后得到的每個聚類再次進行聚類分析，聚類中心點以及每個聚類所占比例均沒有明顯的差別。

7 結論

本文中共統計數據7854條：概率論與數理統計（理工類）課程學生成績1871條，微積分（經管類）課程學生成績1684條，微積分（理工類）學生成績1725條，線性代數（經管類）學生成績539條，線性代數（理工類）學生成績2035條。

對所得數據通過正態分布模型檢驗得到，學生成績并不像預計的一樣服從正態分布。

對數據進行聚類分析發現：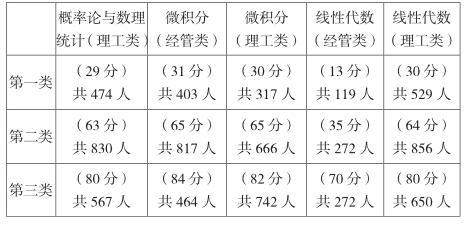

基本上每個課程的學生成績都呈現“不及格—及格—高分”這三個成績區間，且處于“及格”區間的人數多于其他區間。

之后，通過課程、老師、年級分類，再進行聚類分析。分析輸出的結果，發現不同課程、老師、年級的學生成績基本上剛好可以劃分為“不及格—及格—高分”這三個類別。其中不及格的聚點在8～56之間，其中33為眾數。及格的聚點在60～73之間，其中62、64為眾數。高分的聚點在75～87之間，其中77為眾數。

自2010年起到2017年的八年中，不及格學生的成績雖有略微提高，但是變化不大。及格學生的成績則變化較大，提升了6～7分。高分組學生的成績比較穩定，上下浮動不大。

通過課程、老師分類，再進行聚類分析。分析輸出結果顯示，教師的不同對學生成績的劃分并無太大影響，不同課程對學生成績的劃分也不存在太大的影響。

鑒于通過對各個課程的正態分布模型檢驗看到整體雖然不服從正態分布，但通過對各個課程聚類分析后得出的聚類再次進行正態分布模型檢驗，發現各個聚類中的成績是服從正態分布。

因此，對各個課程聚類分析后每個聚類各自再次進行K-Means聚類。通過輸出結果可以看到聚類中心點以及每個聚類所占比例均沒有明顯的差別。由此可得出結論：不同班級、年級、教師之間學生成績分布差異不明顯。

綜上所述，近年來，該校學生公共數學成績60多分人數居多，80分以上高分人數相對較少。原因之一是在時間安排上，十八周課程一結束就開始考試，考試時間、科目密集，學生缺乏充足的考前復習歸納總結時間，使得學生往往考前突擊復習，導致大部分學生考試成績普遍偏低，高分相對較少；近年來學校擴招，降低了生源的準入門檻，導致學生總體素質下降，成績出現在高分區間的數量也就相應下降；另外，學校設置計算總成績的方法是當學生期末成績高于50分，將平時、期中、期末成績加權平均為總成績，導致總成績在50～59分數段的數據缺失。

參考文獻：

[1]高惠璇.應用多元統計分析[M].北京：北京大學出版社，2014：1-419.

[2]范金城，梅長林.數據分析[M].北京：科學出版社，2002：205-241.

[3]薛薇.SPSS統計分析方法及應用[M].北京：電子工業出版社，2013：1-382.

[4]李春林.應用多元統計分析[M].北京：清華大學出版社，2013：1-223.

[5]薛薇.統計分析與SPSS的應用[M].北京：中國人民大學出版社，2014.1-307.

[6]楊維忠，張甜.SPSS統計分析與行業應用案例詳解[M].北京：清華大學出版社，2013：1-412.

[7]馮巖松.SPSS22.0統計分析應用教程[M].北京：清華大學出版社，2015：1-439.

[8]吳贛昌 概率論與數理統計（理工類·第五版） [M].北京：中國人民大學出版社，2017：212-217.

[9]戴維·R·安德森.商務與經濟統計（第八版）[M].北京：中信出版社，2003：505.

◇責任編輯 趙麗斌◇