數形結合百般好，隔離分家萬事休

吳進

摘? 要：華羅庚先生說過：“數缺形時少直觀，形少數時難入微，數形結合百般好，隔離分家萬事休，幾何代數統一體，永遠聯系莫分離。”“數”的準確性和“形”的直觀性，可以引導學生更全面地認識數學本質，發展學生的數學思維，觸發高效的數學學習。

關鍵詞：以形助數;以數解形;數形結合;小學數學

數學是一門研究客觀世界中的數量關系和空間形式的學科，具有抽象性、邏輯性和概括性等特點，而“數”和“形”就是貫穿小學數學課本的兩條基本主線。

■一、以形助數，抽象知識直觀化

現階段，在小學數學學習中，“數”指的是數與代數，包括了數的認識、數的運算、數量關系、常見的量等內容。然而基于學生數學核心素養的培養要求，我們傳統的數與代數的教學就顯得：重數量，輕質量;重過程，輕思維;重內容，輕生活;重形式，輕價值。

小學階段，低年級學生的思維趨向于將數學知識與具體事物或生動表象聯系在一起，高年級學生逐步學會區分概念中的本質與非本質屬性、主要與次要的因素，學會用抽象、科學的定義概括生活表象，思維邏輯性逐漸增強。但是，總體而言，小學生的數學思維仍然趨向于將數學知識與直接的、感性的經驗聯系在一起，具有很明顯的具體形象性。

因此，在小學階段，如何賦予“數與代數”這塊內容更多的趣味性、直觀性、實用性，可以說是我們亟須考慮的問題！結合小學數學幾何圖形直觀形象的特點，我們做了如下嘗試。

1. 數的認識

數的認識，包含了自然數、整數、小數、分數等概念的學習，是小學數學學習中最基本的內容，是學生今后構建數的概念體系、掌握數的運算、探究數量關系的重要基礎。那么如何建立起枯燥概念與直觀圖形的紐帶呢？

我們就以認識“分數的意義”為例。分數的概念：把單位“1”平均分成若干份，取其中一份或幾份的數叫作分數。如果單靠字面含義，難以理解分數的概念，而教材中直觀圖的及時呈現恰好可以提供幫助。例如，聯系第2張圖，學生明白了：把一個長方形看作單位“1”平均分成8份，取其中5份就表示“八分之五”。化抽象概念為具體事例的同時，加深了學生對分數的理解，為接下來學習分數的運算、數量關系的分析打下了堅實的基礎。

2. 數的運算

數的運算指根據一定的數學概念、法則和定理，由一些已知量通過計算得出確定結果的過程。新課標指出，學生運算能力的培養要注重以下幾點：理解運算意義，理解運算算理，掌握運算方法，選擇運算方法解決問題。在傳統的計算教學中，家長、學生、教師更注重掌握運算方法，鑒于其相對抽象、枯燥、死板，學生多采用“題海戰”來強化練習，卻對運算本質知之甚少。

為了發展學生的思維，探尋數學運算的本質，現階段，幫助學生理解運算意義、理解運算算理才是我們計算教學的重中之重。那如何讓枯燥的算理“活”起來，更易于學生理解呢？我們智慧的數學教師，契合小學生思維發展特點，想到了用圖來化解難點。

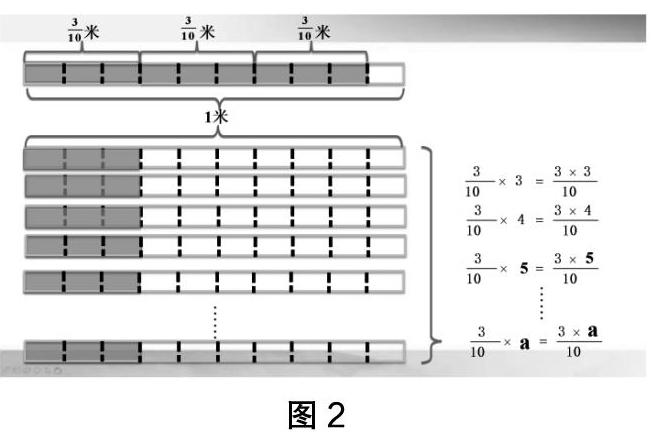
例如，在教學“整數乘分數”中，運算方法是：分母不變，分子與整數相乘的積作為分子。簡單的一句話卻包含了兩個關鍵點：“為什么分母不變？”“分子與整數相乘的積表示什么？”多數學生對此是比較模糊的。而圖形恰好可以形象地說明，其中一個小長方形表示一個“十分之一”米，分子乘分母就是計算有幾個“十分之一”米。由圖可見，“分母不變”是說明分數單位不變，“分子與整數相乘的積作為分子”表示有多少個這樣的分數單位。從算理到算法，從一般到特殊，在幫助學生理解算理的同時，增強了運算學習的直觀性、趣味性。

3. 數量關系

數量關系是從數學問題中總結出來的揭示某些數量之間的本質聯系，并以數量關系式表示這種聯系。因此，學生深刻理解、掌握“數學問題”背后的數量關系，對于解決同類問題，培養“舉一反三”能力，形成對應的解題策略，發展數學思維，就顯得尤為重要了。

為了在復雜問題中，清晰、準確地找到數量關系，我們小學數學中常用的方法之一就是“線段圖”，它有助于將數學問題中數量以及數量之間的關系可視化、直觀化。

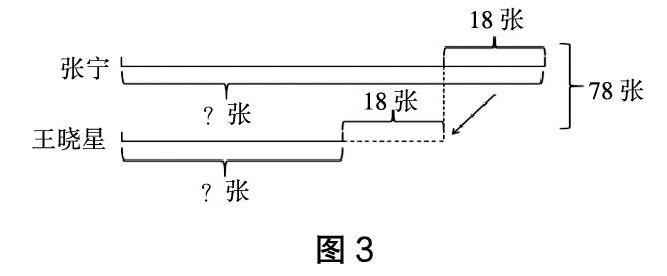
例如，張寧和王曉星一共有78張郵票，張寧給了王曉星18張郵票后，兩人一樣多，那么張寧和王曉星原來各有多少張郵票？這個問題看似比較簡單，然而“張寧給了王曉星18張郵票后，兩人一樣多”這句話很容易讓學生誤以為：張寧的郵票數-王曉星的郵票數=18（張）。但如果將條件和問題整理成一張線段圖，學生可以輕易發現，實則：張寧的郵票數-王曉星的郵票數=36（張）。由此可見，線段圖融合了條件和問題的同時，能夠清晰地呈現數量之間的內在聯系，其表現方式更契合小學生思維的形象性，更有助于學生數學思維的發展。

4. 常見的量

常見的量包括了時間、長度、面積、體積等知識。縱觀小學階段“常見的量”的學習，其抽象性讓學生的體驗感不強，大多數只會生搬硬套，不能夠正確建模和應用。然而，抽象的文字卻與生活實際緊緊聯系在一起，我們數學教師的任務之一就是要架構起它們之間的橋梁。

例如，在教學“認識體積單位”時，常見的體積單位依次有立方厘米、立方分米、立方米，單靠文字，學生難以體驗其實際大小。考慮小學生認知發展水平的直觀形象性，以體驗“1立方分米的大小”為例，一方面我們借助常見的幾何圖形進行理解：棱長是1分米的正方體，體積是1立方分米;另一方面我們借助生活中的物體進行理解：1立方分米相當于1個粉筆盒大小。多角度幫助學生化抽象為具體，讓“冰冷”的知識“鮮活”起來，真正為學生的思想“減負”。

■二、以數解形，表面現象精準化

小學數學學習中，另一條主線是“形”，指的是圖形與幾何，主要包含四部分：圖形的認識、圖形的測量、圖形與變換、圖形與位置。縱觀小學六年級中“圖形與幾何”知識板塊的教學，“圖形與幾何”無論是在學習還是生活中，學生從直觀、表面上去認識它們是比較容易的，但同時也是相對膚淺的。如果有了“數與代數”的支撐，我們就可以進一步深入、精準了解圖形，挖掘圖形的內在價值，為我們解決有關“圖形與幾何”的實際問題搭橋鋪路。比如：

1. 圖形的認識

以“認識長方體”為例。如果沒有數據支撐，我們僅僅只是知道生活中的牙膏盒、油箱、游泳池等類似的幾何形狀是長方體;有了數據支撐，我們便知道長方體有8個頂點、12條棱和6個面，相對的棱長度相等，相對的面完全一樣……從而我們可以依據長方體的特點，自主地制造我們需要的長方體物體。

2. 圖形的測量

以“測量線段的長度”為例。如果沒有數據支撐，我們僅僅只是知道上海去南京很遠;有了數據支撐，我們知道兩地大約相距300公里，開車大約需要4小時，坐高鐵大約需要一個半小時，乘飛機大約需要1小時……可以幫助人們合理安排時間、合理安排交通出行。

3. 圖形與變換

以“圖形的放大與縮小”為例。如果沒有數據支撐，我們僅僅只是知道照片可以放大或縮小;有了數據支撐，我們知道圖形放大或縮小后，對應邊成比例，形狀才不會發生變化，可以按1∶2縮小，也可以按5∶1放大……依此，拍證件照片時，我們僅需拍一次照片，就可以按需要打印1寸、2寸等不同大小的照片。

4. 圖形與位置

以“確定位置”為例。如果沒有數據支撐，我們僅會用“四面八方”確定大概方向;有了數據支撐，我們可以知道具體位置在什么方向，多少角度，多少距離……例如，當軍艦發現遇難船只在北偏東50°方向12海里處，可以更方便、更迅速地去展開救援。

由此可見，圖形的直觀性、簡潔性確實在某種程度上契合了小學生的認知發展特點，但如果我們的數學學習僅限于此就難免顯得淺薄了;而在數據支撐下，學生可以更深入、更細致、更精準地去了解圖形、了解客觀世界，體驗數學學習的價值。

■三、數形結合，助推數學問題的有效解決

“數”表示抽象思維，“形”表示形象思維。“數形結合”告訴我們，使抽象思維與形象思維相結合，通過“數”與“形”的互相轉化可以高效解決一系列數學問題。而從上面的交流中，我們也不難體會出“數學結合”思想對我們學習數學知識、解決數學問題、體會數學價值大有裨益。

小學階段，學生的思維以具體形象為主，逐步向抽象邏輯思維過渡，小學生更多地能夠體會到“以形助數，抽象知識直觀化”的優點，若是能夠巧妙地運用“數形結合”思想，往往會使抽象問題直觀化，復雜問題簡單化，達到優化解題路徑，達到事半功倍的效果。而隨著年齡的增長，學段的上升，尤其到了高中、大學階段，學生會對“以數解形，表面現象精準化”的理解更加深刻。因此，我們高年級教學可以適當滲透，待學生以后進一步感悟。