以數(shù)學建模思想培養(yǎng)學生數(shù)學核心素養(yǎng)的教學實踐

許晶

【摘要】新課程改革對課堂教學提出了更高的要求，要求教師不僅要提高學生的數(shù)學能力，還要在教學過程中培養(yǎng)學生的核心素養(yǎng)能力，促進學生發(fā)展.在高質(zhì)量數(shù)學課堂的培養(yǎng)下，學生不僅要掌握數(shù)學方法，還要運用數(shù)學思想與數(shù)學思維解決實際問題，這就要求教師研究更好、更具有效率的教學方法.數(shù)學建模思想作為數(shù)學思想方法中的重要組成部分，其在初中數(shù)學教學中的運用備受教師的關(guān)注.基于此，筆者從四個方面研究如何在數(shù)學教學過程中滲透數(shù)學建模思想，從而培養(yǎng)學生數(shù)學核心素養(yǎng)，讓學生更好地學習數(shù)學.

【關(guān)鍵詞】核心素養(yǎng);初中數(shù)學;建模思想

引 言

數(shù)學建模是一門應用數(shù)學，是運用數(shù)學的語言與方法，通過抽象建立出來的模型解決問題的一種思想方法，是解決數(shù)學問題強有力的手段.在初中數(shù)學教學過程中，幫助學生體會建模思想，提高學生的建模能力，有利于學生明確解題思路，摸索解題技巧，從而做到化難為易，化繁為簡，輕松解決問題，實現(xiàn)學以致用的目的.

一、滲透建模思想，梳理抽象關(guān)系

要想具備建模思想，就要求學生充分掌握數(shù)學基礎(chǔ)知識，為體會建模思想做好扎實的基礎(chǔ)，從而加深對建模過程的印象，培養(yǎng)學生的建模能力.基于此，教師在教學過程中應探索滲透建模思想的教學方法，可以從建模過程入手，將建模思想引入當中，幫助學生理解.教師可以將生活中的問題引入課題，一來可以有效激發(fā)學生的學習興趣，二來利用生活中的問題，便于學生理解，可以很好地幫助學生建立抽象關(guān)系，并將建模過程展示給學生，加深學生對建模的理解，從而有效培養(yǎng)學生的核心素養(yǎng)能力.

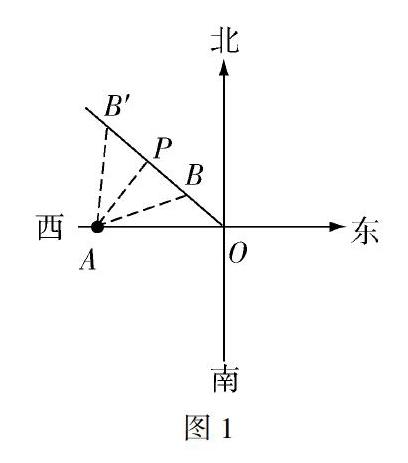
例如，某次臺風中心在O地，臺風中心以25千米/時的速度向西北方向移動，離臺風中心240千米的范圍內(nèi)都會受臺風影響，某A市在O地的正西方向320千米處，問：A市是否會受此次臺風的影響？若會，將持續(xù)幾個小時？

在這種題型的教學中，教師可以引導學生結(jié)合解直角三角形的問題，畫出示意圖如圖1，通過幾何建模的思想去解題.

二、拓展建模思維，培養(yǎng)學生解決問題的能力

在應用建模思想培養(yǎng)學生數(shù)學核心素養(yǎng)能力的過程中，拓展學生的建模思維也是很重要的方面，這有助于激勵學生的學習熱情，讓學生沉浸在學習的快樂海洋中，從而提高學生的創(chuàng)新思維，提高學生獲取知識的能力，為學生今后的發(fā)展提供強有力的幫助.如何拓展學生的建模思維呢？教師可以試著引導學生從多個角度思考問題.

例如，在學習“實際問題與一元一次方程的應用——配套問題”這一內(nèi)容時，為了讓學生更好地掌握和應用知識，培養(yǎng)學生分析問題、解決問題的能力，拓展學生建模思維，教師可引導學生從多角度思考問題.如：某車間有22名工人，每人每天可以生產(chǎn)1200個螺釘或2000個螺母.1個螺釘需要配2個螺母，為使每天生產(chǎn)的螺釘和螺母剛好配套，應安排生產(chǎn)螺釘和螺母的工人各多少名？這實際上是一個配套問題，解決這類問題，我們可以從三個角度來分析.第一個角度是“成倍”關(guān)系，1個螺釘需要配2個螺母，要使每天生產(chǎn)的螺釘和螺母剛好配套，也就是說，螺母的總數(shù)量是螺釘?shù)?倍，即螺母的總數(shù)量=2×螺釘?shù)目倲?shù)量.第二個角度是“成比”關(guān)系，螺釘?shù)目倲?shù)量∶螺母的總數(shù)量=1∶2.第三個角度是“成套”關(guān)系，1個螺釘和2個螺母組成了一套產(chǎn)品，如果將1個螺釘為1組，2個螺母為一組，那么當螺釘和螺母的組數(shù)相等時就配套了，螺釘總數(shù)量÷1=螺母總數(shù)量÷2.

通過對本題的學習，從“成倍”“成比”“成套”這三種不同的思路分析，形成了“配套問題”的解題思路，建立了數(shù)學模型，拓展了學生的建模思維，有效提高了學生解決問題的能力，從而培養(yǎng)學生的數(shù)學核心素養(yǎng)能力.

三、加強建模應用，促進學生全面發(fā)展

數(shù)學來源于生活，又服務(wù)于生活.因此，加強學生建模思想的教學，培養(yǎng)中小學生核心素養(yǎng)能力，都是為了學生能在生活中應用數(shù)學知識.因此，在初中數(shù)學教學過程中，教師應當加強建模的應用練習，從而使得建模思想在教學中得到充分利用，即有助于提高學生的數(shù)學建模能力，又能促進學生的全面發(fā)展.此外，在傳統(tǒng)的數(shù)學課堂教學中，課堂氛圍往往過于沉悶，多數(shù)都是教師采取主導的形式對學生進行知識灌輸，促使學生被動接受數(shù)學知識，不僅無法有效推動學生數(shù)學核心素養(yǎng)的形成，也讓學生思維存在一定的局限性.為了培育學生核心素養(yǎng)，推動學生建模應用能力，教師應改善教學方式，對教學路徑進行科學、合理的設(shè)計，基于趣味性教學設(shè)計，調(diào)動學生主觀能動性.初中階段的學生有著濃烈的好奇心、探索欲望，教師可利用這一點，充分調(diào)動學生進行建模思想的學習.由于學生理性思維處于發(fā)展中階段，其更多用理性思維進行學習，在一般的數(shù)學學習過程中，學生接受的知識都是枯燥、乏味的數(shù)學計算教學，不僅打擊了學生的積極性，也讓學生失去了自主思考、自主學習的動力.而基于建模思想構(gòu)建的教學則不然，由于建模思想即抽象化思維處理，在學生應用思維的過程中具有更為廣泛的空間，不僅迎合了學生的感性思維，也讓學生獲得了豐富的情感體驗，發(fā)展了學生的思維拓展能力.教師可基于生活化策略，引導學生應用建模思維解決實際數(shù)學問題.

例如，在教授“增收節(jié)支”這一內(nèi)容時，教師可以將社會熱點問題引入課堂中：我們學校今年總?cè)藬?shù)為3180人，比去年增加了6%的人數(shù)，其中男生增加了5%，女生增加了8%，請問去年男生和女生各為多少人.

通過已知條件可得出去年學生人數(shù)總和為3000人，假設(shè)去年男生人數(shù)為x人，女生人數(shù)為y人，可得方程：x+y=3000，1.05x+1.08y=3180，聯(lián)合解方程，得出男生人數(shù)為2000，女生人數(shù)為1000.通過二元一次方程組模型的建立，讓學生體會到建立模型的作用.

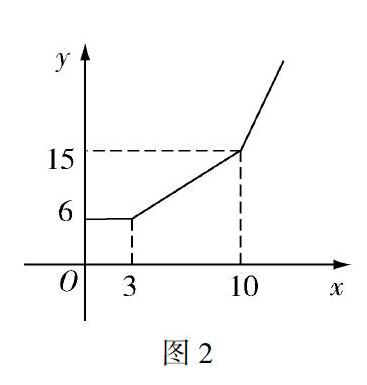
又如，某市共享汽車的出現(xiàn)可方便市民出行，其收費標準為：3千米內(nèi)收費6元;3千米到10千米之間每千米收1.3元;10千米以上每千米收取1.9元.在這一問題中，為了便于學生思考，教師可以采取繪圖方法進行教學.此問題實質(zhì)上屬于經(jīng)典的函數(shù)問題，共享汽車的收費y與行駛路程的千米數(shù)x相關(guān)，如圖2.

在這一教學過程中，我們可以明顯看出，數(shù)學問題中的數(shù)據(jù)與圖像有著較強的關(guān)系，在建模思想中，數(shù)形結(jié)合也是較為關(guān)鍵的核心因素，學生在應用建模思想時，可以有效地簡單化、形象化較為復雜的數(shù)學關(guān)系，即得出結(jié)論：假設(shè)x大于10，總收費是6+1.3×（10-3）+1.9×（x-10）.這樣一來，學生的數(shù)學探究學習得到良好的引導，學生也可以更好地抽象數(shù)學知識.

四、應用情景教學提高學生建模意識

在初中數(shù)學教學中，教師不可避免會遇到這樣的問題，學生只是無意識、機械性地進行模仿學習，沒有學習思想、學習意識的全面提升、鍛煉，導致學生學到的數(shù)學思想存在一定的局限性，不僅不利于培養(yǎng)學生的思維發(fā)展，長此以往也會讓學生出現(xiàn)厭惡、抵觸等不良心理因素.因此，教師可積極利用情境教學這一措施，調(diào)動學生積極性，促使學生可以積極自主地參與到教學內(nèi)容中，豐富學生的思維發(fā)展，并引導學生應用建模意識解決問題，充分提高學生的建模應用能力.在情境教學中，情景的概念較為廣泛，其實施策略也存在差異.教師在構(gòu)建情景教學中，應充分考慮學生的生活認知、情感認知，確保學生在學習的過程中可以有效地調(diào)動積極性.教師可利用生活中較為常見的情景構(gòu)建問題，例如，公交車是否需要辦年卡的問題.教師可基于這一問題引導學生積極思考，如，王老師每天乘58路公共汽車回家，每一次來回需要花費10元錢，如果辦年卡需要工本費20元，但每次乘坐公共汽車會打6折，同學們，你們認為王老師需要辦年卡嗎？并在此基礎(chǔ)上設(shè)立問題：假設(shè)一年乘車x次，你會用代數(shù)表示不辦年卡與辦年卡的區(qū)別嗎？這種代入感較強的問題可以有效地引導學生積極回答，如y1=10x和y2=6x+20，然后根據(jù)代數(shù)式的大小關(guān)系，就x的取值范圍進行深入討論.從真實的情景構(gòu)建出發(fā)，潛移默化地讓學生體驗建立一次函數(shù)模型解決問題，不僅增強了學生的應用能力，也讓學生在日常生活中針對此類問題具有良好的建模意識.此外，在構(gòu)建情景的過程中，教師應從開放性、交互性等方面出發(fā)，促使學生在聽到問題后思維保持高度活躍，進而積極自主探索數(shù)學領(lǐng)域，推動學生發(fā)展，加強學生數(shù)學建模能力的提升.因此，教師在開展數(shù)學課堂教學中，應積極利用情景構(gòu)建，利用生活案例、電教案例等，引導學生基于多元化角度出發(fā)思考問題，這不僅可以培養(yǎng)學生的數(shù)學建模能力，也培養(yǎng)了學生形象化的數(shù)學探究意識，調(diào)動學生學習建模思想的積極性，構(gòu)建和諧師生關(guān)系的同時，豐富學生的數(shù)學體驗，加快學生核心素養(yǎng)的形成.

五、結(jié)束語

總而言之，培養(yǎng)學生建模思想是培養(yǎng)學生數(shù)學核心素養(yǎng)能力的關(guān)鍵之一，是核心素養(yǎng)下對初中數(shù)學教學的要求.教師應結(jié)合教學情況和生活實際去設(shè)計相關(guān)教學內(nèi)容，激發(fā)學生的學習動機，有意識地培養(yǎng)學生的建模思想.學生通過觀察、分析，建立模型來解決問題，其應用能力得到培養(yǎng)，從而使得學生的數(shù)學核心素養(yǎng)能力得到發(fā)展，對學生今后的發(fā)展也有很大的幫助.

【參考文獻】

[1]張中華.淺議數(shù)學核心素養(yǎng)中數(shù)學模型能力的培養(yǎng)[J].上海中學數(shù)學，2018（11）：3-5.

[2]王東俊.淺議中學數(shù)學核心素養(yǎng)的培養(yǎng)方略[J].科教導刊（電子版），2017：89.

[3]謝正新.淺談中學生數(shù)學核心素養(yǎng)的培養(yǎng)[J].甘肅教育，2018.