化靜為動，發展空間觀念

曹冠軍

【摘? ?要】數學學習是一個“做數學”的過程，靜態知識動態化，可以促進學生對知識的理解和應用。挖掘圖形中的動態因素，引導學生用“運動變化”的眼光看待問題，可以幫助學生形成“運動變化”的學習意識和思維習慣。具體可從以下策略入手：動態展示圖形的形成過程;動態剖析圖形的變化瞬間;動態溝通圖形的轉化關系。以促進學生對圖形的本質認識，發展空間觀念。

【關鍵詞】化靜為動;圖形與幾何;空間觀念

皮亞杰的研究表明：靜態表象只能產生物理經驗，動態表象是學習數理——邏輯經驗生成的源泉。讓靜止的圖形動起來，化抽象為直觀，有利于學生直觀洞察、分析推理、發現本質，對圖形形成深刻表象，進而深化轉化思想，構建知識體系，培養學生化靜為動的思維方式。

一、動態展示形成過程，形成深刻表象

教師通過動態展示，運用平移、旋轉、軸對稱等幾何變換方法，可以直觀地呈現圖形變化、形成的過程，引導學生溝通和感受圖形之間的關系，形成深刻表象，促進對圖形的本質理解，完善知識結構，發展空間觀念。

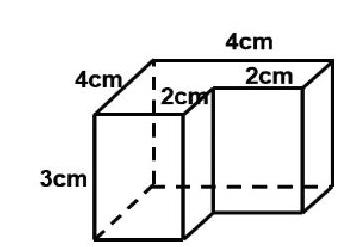
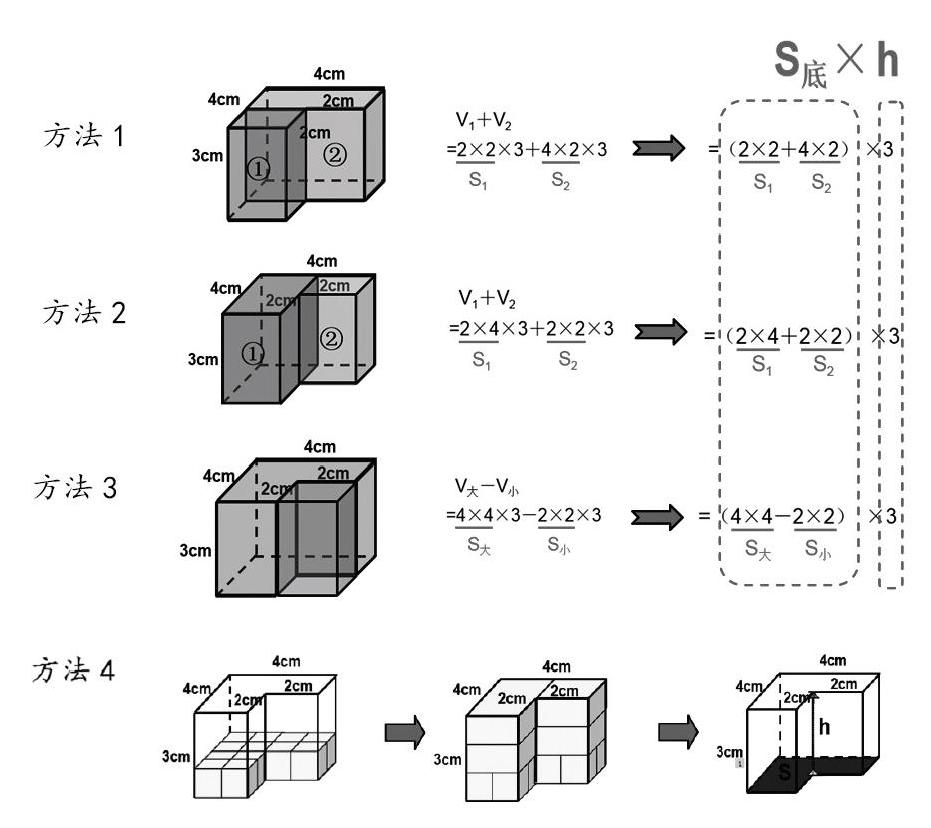
如“柱體的體積”教學中，要計算立體圖形（如右圖）的體積，學生可能會運用不同的方法：

方法1—方法3，運用的是“割補法”，方法4則是通過單位立方體的層層“累加”得出結果。通過溝通不同方法間的聯系，學生體會到如果每一層的體積單位相同，那么不規則的立體圖形也可以是一層一層體積單位的累加，用底面積×高的方法計算，立體圖形在疊加中動了起來，學生更加深刻地理解，在求不規則柱體體積時可運用不同的轉化方法，讓數學學習溫故而知新。

之后教師還可以通過這樣的題目進一步引導學生對不規則立體圖形進行正反辨析，以完善和深化學生對柱體概念本質的理解，形成深刻的表象。

下列哪些圖形的體積可以用“V=Sh”來計算。

通過找到底面的體積單位，引導學生觀察是否可以一層一層地累加上去，在平移過程中圖形的形狀、大小不變。尤其是圖形⑥和圖形⑦的展示，進一步豐富了柱體概念，拓寬了學生的視野。

二、動態剖析變化瞬間，深化轉化思想

教師在教學中應給學生提供豐富的“動態素材”，讓學生通過動手實踐，直接感知圖形的特點，體驗圖形的變化過程，引導學生通過操作與想象相結合的方式去觀察與思考問題，從而積累豐富的活動經驗，深化轉化思想，進而對圖形有更深刻的認識和感受，發展空間觀念。

如在“三角形等積變形”的教學中，教師呈現學習任務：以BC為底，畫出與△ABC面積相等的三角形（如右圖）。請獨立完成，并清楚地表示出三角形的高。

交流反饋：

師：比較這三種方法，哪種更簡潔？

生：添上兩條平行線的方法3。

師：為什么添上平行線更加簡潔？

生：不需要量高，高都一樣長。

生：這些高就是兩條平行線之間的距離。

師小結：剛才量高的方法，如果量得準確一點，得到的這些三角形的頂點都會在上面這條平行線上，并且這些三角形的高就是兩條平行線之間的距離。

師：BC底不動，現在把三角形的頂點A向左移動，它會是一個什么三角形？（銳角三角形，直角三角形，鈍角三角形）

師：把頂點A向右移動。像這樣的三角形可以畫多少個？

師：在三角形的頂點移動的過程中，你發現了什么？

師小結：我們把這些三角形叫作等底等高的三角形，等底等高的三角形面積相等。在兩條平行線之間，如果三角形的底相同，我們只要移動底對應的頂點，就可以畫出無數個等底等高面積相等的三角形。

在教學中，激活、利用與提升學生已有的經驗非常重要。教師引導學生展開自主探究，并通過有層次的展示交流，幫助學生發現這些三角形的頂點都在上面一條平行線上，三角形的高就是兩條平行線之間的距離，從而引出平行線中底不動、頂點移動的過程。化靜為動，學生在比較中感知、內化等底等高的三角形模型的表象，為三角形的等積變形做鋪墊。

這一素材還可以再次被利用，讓學生的思維得到延續。

呈現要求：畫出與這兩個三角形面積之和相等的一個大三角形。

交流反饋：

生：方法1中，①號圖形的頂點移動到和②號的頂點重合，①號圖形與移動后的圖形同底等高面積相等，所以①和②的面積之和就是圖中陰影部分三角形的面積。

師：在這個轉化過程中，誰動了，誰沒動？

生：①號動了，②號沒動。

……

師：剛才這兩種方法有什么共同點？

生：只動了一個三角形。

師：但是在轉化過程中，這條底始終不動。

生：方法3中，①號②號的頂點都移動到中間某一點，移動后左邊三角形和①號圖形同底等高，右邊三角形與②號圖形同底等高。因此陰影中三角形的面積就是原來①號和②號的面積之和。

師：現在①號圖形和②號圖形都動了，但其中什么跟前面一樣一直都沒動？

生：底邊沒動。

師小結：三角形轉化成與它等底等高面積相等的三角形，這樣的轉化叫作三角形的等積變形。這三種方法都有一個共同點：這條底邊始終不動。兩條平行線之間，三角形等積變形的過程中，它們的頂點在移動，最后頂點重合在一起，組成了一個大三角形。在此基礎上學生還感受到，只要以兩個圖形的底的和為底，上頂點沿著上面這條平行線任意移動，得到的所有三角形的面積都是原來兩個三角形面積的和。這里把前面環節中內化的模型表象外顯出來，以此進一步深化表象，學生更深刻地理解三角形等積變形的本質，思維在圖形運動的過程中更加靈活。

三、動態溝通轉換關系，構建知識體系

動靜結合的想象，少一些直觀演示，多一些空間想象，引導學生在腦海中對圖形進行提取、改造、重組，建立空間表象，動態溝通圖形間的關系，有效建構知識體系，使學生形成完整的數學思維體系，發展空間觀念。

如“圓錐的拓展練習”教學中，教師提出以下問題：如果直角△ABC的頂點A沿著中間這條平行線向右移動1.8cm（或向左移動1.2cm），它變成了一個什么三角形，繞BC旋轉后的體積是多少？

師：三種不同類型的三角形繞BC旋轉一周，在求所形成的圖形體積的過程中，有什么相同之處？

生：都可以把頂點到旋轉軸的距離作為圓錐的底面半徑，旋轉的那條邊作為高，轉化成一個大圓錐來求體積。

師：如果三角形的頂點沿著平行線的垂線向下移動到A1，并繞BC旋轉一周的體積是多少？

生：都可以轉化成底面半徑是4.8，高是10的圓錐，體積不變。

師：如果繼續往下移動到A3，體積還會不變嗎？

生：這個圖形的體積是大圓錐的體積減去小圓錐的體積：7.68π×（10+x）-7.68πx=76.8π。體積還是不變。

師：三角形頂點A移動的過程中，你發現了什么？

生：體積始終不變。體積與BC的長度和BC邊上的高有關。

生：我們都可以把它們轉化成以BC邊上的高為底，BC為高的一個圓錐來求體積。

頂點A在橫向、縱向移動的過程中，通過觀察、比較不同類型的三角形分別繞BC旋轉一周后圖形的體積，溝通方法間的共性，經歷具體到抽象的概括過程，引導學生對方法進行總結和歸一：把頂點到旋轉軸的距離作為圓錐的底面半徑，旋轉的那條邊作為圓錐的高，最后求圓錐的體積。

之后還可以繼續呈現任務：如圖，兩組平行線互相垂直，△ABC的兩條邊正好在兩組平行線上，如果△ABC的頂點C向下移動，并繞L2旋轉一周，所形成的圖形的體積是多少？

生：我們可以這樣想，這相當于圓柱里面削去了兩個等底的小圓錐，也就是相當于削去了一個與圓柱等底等高的圓錐，剩下的部分就是圓柱體積的[23]。

師：如果頂點C繼續往下移動呢？圖形的體積還會不變嗎？如果頂點C向下移動x厘米，圖形旋轉后的體積是多少？

生：圖形的體積是大圓柱體積的[23]減去小圓柱體積的[23]：[23]×9π×（8+x）-[23]×9πx=6π×（8+x）-6πx=6π×（8+x-x）=48π。體積始終不變。

頂點C移動到C'的過程中，引導學生逆向思考，深刻認識圖形的體積始終是圓柱體積的[23]，繼續深入探究，如果C繼續下移，通過計算發現C在L2上移動的過程中，體積始終不變，有效地溝通了三角形沿邊、沿頂點旋轉后圖形間的關系，構建知識體系。

綜上所述，化靜為動，讓學生學會“動態地想”，能“動態地想”，不斷創設讓靜止的圖形動起來的機會，為學生創設想象的空間，可以有效提升學生的思維品質，發展空間觀念。

參考文獻：

[1]袁曉萍.學會向學生借智慧[M].杭州：浙江教育出版社，2018.

（浙江省杭州錢塘新區臨江新城實驗學校? ?310018）