高中數學選擇題精選

朱華偉

點評：本題主要考查集合中元素的性質，屬于基礎題。解題時要認真審題，仔細解答，注意不要遺漏a=0的情況。

點評：本題主要考查復數的實部和虛部的定義，兩個復數代數形式的乘除法，虛數單位i的冪運算性質。

點評：根據流程圖（或偽代碼）寫出程序的運行結果，是算法這一模塊最重要的題型，其處理方法是：①分析流程圖（或偽代碼），從流程圖（或偽代碼）中，既要分析出計算的類型，又要分析出參與計算的數據（如果參與運算的數據比較多，也可使用表格對數據進行分析管理）;②建立數學模型，根據第一步分析的結果，選擇恰當的數學模型;③解模。

點評：本小題設計巧妙，綜合考查定積分和二項式定理，是一道以小見大的中檔題，不可小視。

分析：求出f（x）的單調區間和值域，得出f（x）的最大值與單調區間端點的關系，從而得出a的范圍。

點評：本題主要考查利用導數研究函數的單調性、極值與最值、等價轉化方法、方程與不等式的解法，考查同學們的推理能力與計算能力，屬于難題。

點評：本題主要考查函數的奇偶性及函數的單調性，同時考查同學們的分析問題能力和運算求解能力，屬于中檔題。

點評：本題主要考查數列的綜合應用，解題時要認真審題，仔細解答，注意挖掘題設中的隱含條件，合理地進行等價轉化。

點評：本題主要考查一元二次不等式的解法、二次函數的圖像，考查分類討論思想、數形結合思想與計算能力，屬于中檔題。

點評：本題主要考查正弦定理的運用及三角函數值域的求法，關鍵是由已知求出A的范圍。

分析：根據圖像求出φ的值，再由“左加有減”法則判斷出函數圖像平移的方向和單位長度。

點評：本題主要考查三角函數的函數圖像，根據函數圖像求解析式，函數y=A sin（ωx+φ）的圖像變換規律，注意應用正弦函數圖像的關鍵點進行求解，考查了讀圖能力和圖像變換法則，屬于中檔題。

12.△ABC的內角A，B，C的對邊分別為a，b，c，若2bcos B=acos C+ccos A，b=2，則△ABC面積的最大值是（ ）。

點評：本題主要考查正弦定理、余弦定理、基本不等式、三角形面積公式在解三角形中的應用，考查轉化思想，屬于中檔題。

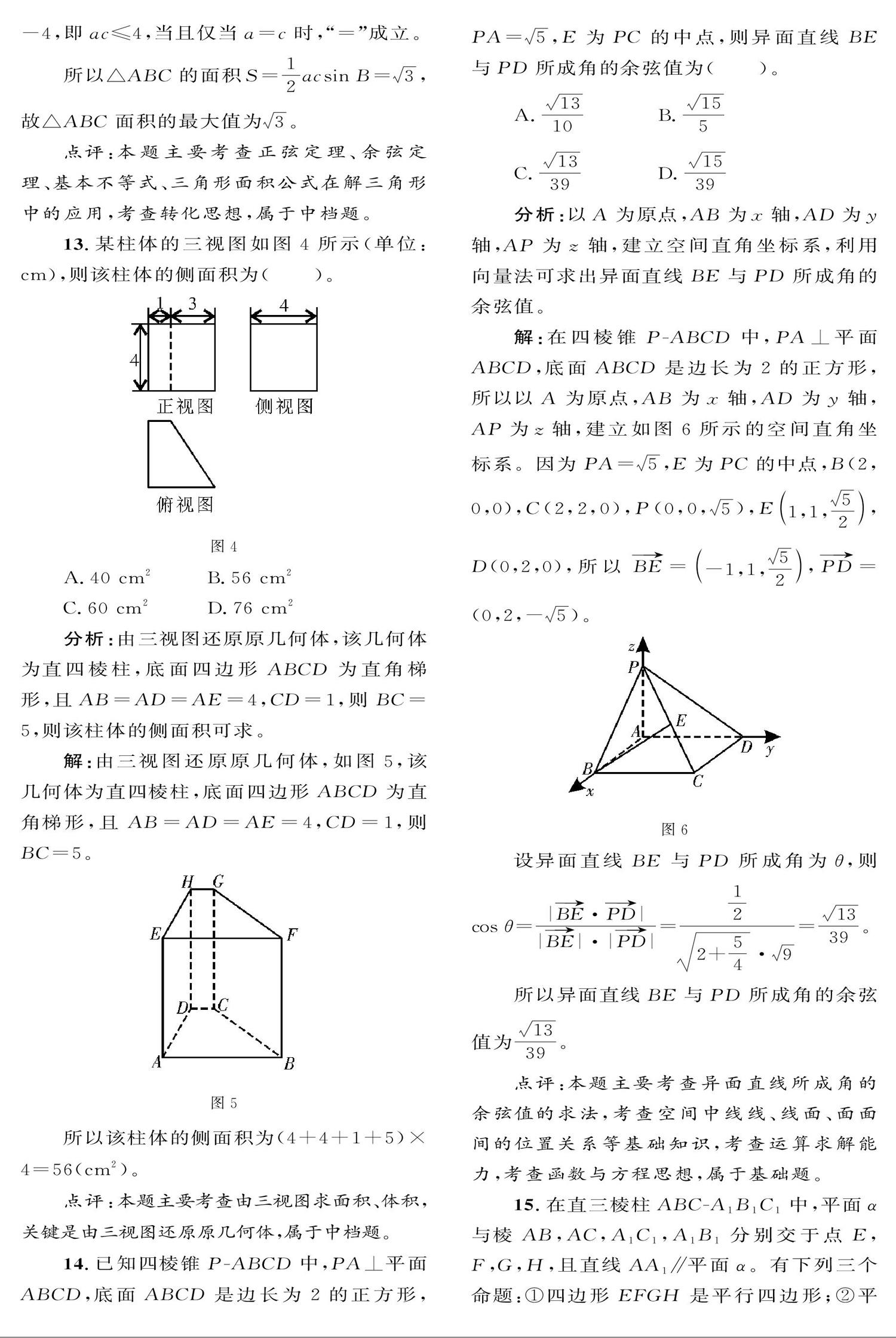
13.某柱體的三視圖如圖4所示（單位：crn），則該柱體的側面積為（ ）。

A. 40 cm2

B.56 cm2

C.60 cm2

D.76 cm2

分析：由三視圖還原原幾何體，該幾何體為直四棱柱，底面四邊形ABCD為直角梯形，且AB =AD =AE=4，CD =1，則BC=5，則該柱體的側面積可求。

解：由三視圖還原原幾何體，如圖5，該幾何體為直四棱柱，底面四邊形ABCD為直角梯形，且AB =AD =AE=4，CD=l，則BC=5。

所以該柱體的側面積為（4+4+1+5）×4=56（cm2）。

點評：本題主要考查由三視圖求面積、體積，關鍵是由三視圖還原原幾何體，屬于中檔題。

14.已知四棱錐P-ABCD中，PA上平面ABCD，底面ABCD是邊長為2的正方形，PA=√5，E為PC的中點，則異面直線BE與PD所成角的余弦值為（ ）。

分析：以A為原點，AB為x軸，AD為y軸，AP為z軸，建立空間直角坐標系，利用向量法可求出異面直線BE與PD所成角的余弦值。

點評：本題主要考查異面直線所成角的余弦值的求法，考查空間中線線、線面、面面間的位置關系等基礎知識，考查運算求解能力，考查函數與方程思想，屬于基礎題。面a∥平面BCCiBi;③平面a⊥平面BCFE。其中，正確的命題是（ ）。

A.①②

B.②③

C.①③

D.①②③

分析：在①中，由AA，∥EH∥GF，知四邊形EFGH是平行四邊形;在②中，平面a與平面BCClBi平行或相交;在③中，EH⊥平面BCEF，從而平面a⊥平面BCFE。

點評：本題主要考查命題真假的判斷，解題時要認真審題，注意空間中線線、線面、面面間的位置關系的合理運用，屬于中檔題。

分析：對于A，延長CB，DE交于H，連接A1H，運用中位線定理和線面平行的判定定理，可得BM∥平面AiDE，即可判斷A;對于B，運用平行線的性質和解三角形的余弦定理，以及異面直線所成角的定義，即可判斷B;對于C，連接A1O，運用線面垂直的判定定理和性質定理，可得AC與DE垂直，即可判斷C;對于D，由直角三角形的性質，可得三棱錐A1-ADE外接球球心為0，即可判斷D。

點評：本題主要考查命題的真假判斷與應用，考查線面、面面平行與垂直的判定和性質定理，考查同學們的空間想象能力和推理能力，屬于中檔題。

點評：本題主要考查橢圓的標準方程及其性質、直線與圓錐曲線的位置關系、一元二次方程的根與系數的關系、三角形面積計算公式等基礎知識，考查同學們的推理能力與計算能力，屬于難題。

點評：本題主要考查圓錐曲線的綜合，解題的關鍵是根據兩個圓錐曲線本身的對稱性及拋物線y2 =8x的性質求出A，B的坐標，得到關于參數a，b的方程，做題時一定要注意從條件中挖掘出有價值的線索來。

（責任編輯 王福華）