想象力：促進兒童思維發展的重要基石

姚蕊

摘要：兒童善于想象，在數學教學中可以發揮兒童想象之長，通過豐富表象積累素材、類比聯想形成技能、試誤學習構建場域等途徑，進一步發展兒童的想象力。以想象力的發展促進兒童數學形象思維與抽象邏輯思維的發展，為創造力的培養構筑堅實的基石。

關鍵詞：想象力;創造力;思維發展

中圖分類號：G623.5 文獻標志碼：A 文章編號：1673-9094（2019）10A-0077-03

想象是思維的一個特殊范疇，是人對已有的表象進行加工，創造出新形象的思維過程。“想象力則是個體為達到一定的目的、完成某項任務或滿足某種期待而借助表象、符號形成某種難以借助五種感官感受到的事物的心智圖景或情境能力。通俗地講，想象力就是個體通過想而改造、重組表象，在頭腦中創造一個念頭或思想畫面的能力。” [1]兒童善于想象，在數學教學中發揮兒童的想象之長，進一步發展他們的想象力，可以為數學的形象思維與抽象邏輯思維搭建溝通的橋梁，促進兒童以形象思維為支點，不斷提升抽象思維能力，實現數學思維的全面發展。

一、豐富表象，積累想象的素材

想象是依賴腦內已有的記憶影像及表象而展開的思維活動。表象是想象的基本材料，表象的形成、積累和豐富是想象力發展的基礎。發展兒童的想象力，需要鏈接他們的生活世界、激活兒童的已有經驗，在“數”與“形”的探究中實現兒童表象材料的儲備。

1.數形相合，構造表象

數是對客觀世界中“量”的抽象產物，開展數的認識的教學，需要遵循兒童的思維特點，在經歷情境化、直觀化的過程中形成數形相合、數境相融的表象材料，為理解數的意義提供直觀支撐，為想象力的發展積累素材。

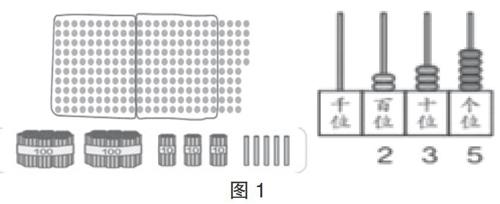
認識自然數時，可以借助小棒、木塊、點子圖、計數器等直觀模型，讓抽象的數看得見，摸得著。比如，認識千以內的數，在兒童經歷了點子圖上圈一圈、用小棒擺一擺、計數器上撥一撥的過程后（如圖1），數形相合的表象留存在腦海，“235”這個數就變得具體、真實、鮮活了，不再是一個無意義的、抽象的符號。在認識分數、小數、負數時，則可以通過創設情境、多元表征、模型構造等方式，讓抽象的數經驗化、具體化。比如，《認識負數》一課的教學，新課伊始之時，讓學生自主表達對“-2”的理解。學生們鏈接生活、聯系已知展開想象，有的進行情境創編，有的用實物圖表意，也有的用運算來求解，多視角的解讀，構成了一組多維度的表象材料，在促進對負數認知的同時，也為想象的展開提供了豐富的材料儲備。

當抽象的數與直觀的模型、具體的情境建立關聯，形成數形相合、數境相融的表象材料，不僅讓抽象的數變得可知、可感，同時還為兒童“看數想形”“看數生意”的想象提供了可能。

2.形意相融，豐富表象

圖形也是客觀現象抽象的產物。認識圖形的教學，通常從兒童熟悉的情境入手，選取典型的實物模型，在觀察、分析、比較的基礎上，逐步抽象概括形成對圖形關鍵特征的認知。之后還需引導他們依據形成的概念展開想象、判別圖形、創生表象，不斷擴充例證，豐富外延。比如，二年級時要初步認識角、直觀認識平行四邊形，因為只是初步認識、直觀把握，所以教學中不揭示圖形的本質特征。學生在形成對角、平行四邊形的基本認識后，通過圖形識別豐富的正反例證（如圖2），使腦內的圖形形象不斷得到矯正和調試，這對于兒童形成清晰、準確的圖形表象顯得尤為重要。

想象不是憑空產生的，它依賴于兒童頭腦中的表象材料，材料的數量、準確性和清晰度都關系著加工與改造的效果。因此，在數量關系與空間圖形的探究活動中，適時地幫助兒童積累豐富多元、清晰可感的表象材料，才能為實現真正的數學想象構筑平臺，借助想象的發展實現兒童思維與抽象的數學世界的溝通與關聯。

二、類比聯想，習得想象的技能

想象力是創造力的起始階段，想象本身就具有創造性的成分，而實現創造依賴于頭腦內已有影像與表象的重組與改造。表象的重組與改造則需要類比和聯想的思維方法作為工具支撐。它使在場的與不在場的東西相互關聯、相互溝通，構成想象的空間。

1.借助類比尋找思路，生發想象

所謂類比就是尋找兩類事物的異同點，加以綜合，從而發現它們共同的本質屬性的方法。運用類比有助于兒童在比較中將原有的學習經驗遷移到新的學習情境中去，根據不同材料生發想象，在對形象材料的加工改造中實現問題的解決。

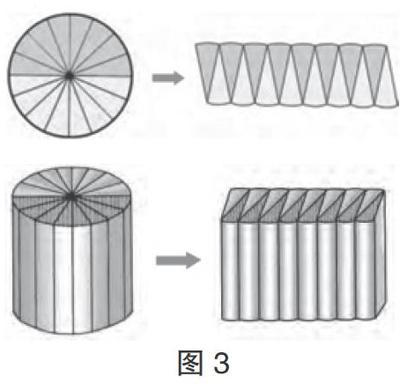
六年級時學生學習《圓柱的體積》，因為圓柱的兩個底面是圓形，所以圓柱體與圓是具有關聯度的數學表象。教學中，教師有意識地引導學生類比兩者，他們便可以從圓的面積推導中獲得靈感，由此，適度地想象加工，推及到圓柱體積公式的推導中（如圖3）：將圓柱的底面平均分，把圓柱切分為若干等份，拼成近似的長方體，尋求圓柱和拼成的長方體之間的關系，再聯系長方體的體積計算公式，便可推導獲得圓柱的體積計算公式了。

2.借助聯想實現轉化，拓展想象

聯想是類比的進一步發展，是一種發散式的思維。學會聯想有助于兒童面對新問題時進行發散式的思維聯結，為創造性地問題解決提供多種路徑。

五年級時學生學習《小數乘整數》，教材呈現的是賣西瓜的現實情境，夏天時西瓜0.8元/千克，問買3千克西瓜要多少元？這樣顯性的情境以及題目中隱含的數量關系都會帶給兒童思維的觸發。如果由0.8×3聯想到乘法的意義，學生便可能用加法運算0.8+0.8+0.8=2.4（元），獲得結果;如果由0.8元聯想到8角，就有可能轉化成整數乘法解決問題，即0.8元=8角，8×3=24（角），24角=2.4元;如果能和計數單位建立關聯，便可獲得3個0.8合并起來就是24個0.1，也就是2.4的結論。兒童基于在場的數學信息展開聯想，建立的聯系不同，對表象加工和重組的方式不同，解決問題的路徑也就不同。

類比是發現的源泉，聯想是創造的基石。在類比與聯想中，把不同的形象材料——顯性的與隱蔽的，過去的與今天的……交織、匯集在一起，為想象的展開鋪就方法的道路，為想象力的發展奠定堅實的基礎。

三、試誤學習，構筑想象的場域

試誤學習，實際上是一種發現學習，它允許兒童在自主探究、自我嘗試中發現知識，掌握方法，感悟思想;在迷茫困頓、經歷挫折中調整方向，修正不足，獲得正解。它允許兒童不斷地嘗試錯誤，為兒童提供了自由參與、表達、體驗、探究的時空，構筑了想象的場域，重塑了數學課堂的教學樣態。

1.在“是什么”的探究中發現

“數學中存在大量的陳述性知識，如數學概念、運算性質、計算公式、數學規律等。”[2]教學中可以把獲得陳述性知識的學習轉化成對“為什么”的探求，給學生提供試誤發現的機會，讓兒童在“是什么”與“為什么”的因果追溯中發展想象力、提升學習力，養成善問、好問的習慣。

五年級時學生要學習《圓的面積》一課，沒學之前，不少學生已經知曉圓面積的計算方法。此時教學的重心可以放在對“為什么這樣算”的探求上。以轉化思想為引領，引導兒童將圓與已經學習過的平行四邊形、三角形、梯形等直線圖形建立關聯，鼓勵他們在自由想象創造的空間中，動手操作，實踐嘗試，實現對圓的加工與改造。不同的改造路徑會引發不同的公式推導過程，最終，學生們殊途同歸，共同驗證了圓面積計算方法的合理性。探究“圓面積為什么這樣算”的過程是學生借助直觀材料經由想象對圓進行改造，借助直線圖形面積公式經由推理獲得圓面積公式的過程，也是學生的思維由直觀形象向抽象邏輯不斷進階的過程。

2.在“怎么辦”的嘗試中探究

兒童是一個天生的創造者，他們對大千世界萬事萬物充滿著探究的欲望。順應兒童的天性，數學的學習需要跳出“數學”，走進自然，走入社會，在廣闊的世界里發揮數學的用武之地，讓兒童在擬定“怎么辦”的方案里、在嘗試解決問題的過程中，將想象力轉化為行動力落實在問題解決中。

四年級時學生要認識三角形和平行四邊形，他們走進生活尋找原型，結果發現很多物體中有三角形或平行四邊形的元素。在分類對比與實驗研究中，學生們感悟到三角形具有穩定性，而平行四邊形具有不穩定性，生活中一些物品正是利用了圖形的特性而設計完成的。由此，學生們也萌生了做一個小小設計師的愿望。于是，“牙簽建高塔”的比賽應運而生：用木質牙簽和棱長1厘米的胡蘿卜丁為實驗材料，設計搭建框架，以能承受50克的重量為標準，比一比哪個小組的高塔建得最高。學生們運用學習所得，充分利用三角形的穩定性，借由想象得以在形象思維與抽象思維的穿梭中，搭建出以三棱柱、四棱柱、五棱柱等為主體的形態各異的復雜結構，把想象力發揮得淋漓盡致。

試誤學習，讓學生在試一試、探一探的場域中親歷知識形成的過程，習得想象方式與學習方式。而想象方式與學習方式的習得，會運用到其他知識的學習中，讓兒童在未來的學習中保持探究與創造的姿態。

想象力具有發散性和創造性，是創造力的起始階段。沒有豐富的想象力，創造力也難以形成。在數學教學中，通過儲備清晰可感的表象材料，習得類比、聯想的思維技能以及試誤學習構建想象的場域等方式，可以有效地發展兒童的想象力，并促進他們形象思維、邏輯思維和創造能力的發展。

參考文獻：

[1]張志泉，陳振華.教育應助力兒童想象力的發展[J].中國教育學刊， 2019（2）：54.

[2]曾海英.初中數學教科書中的數學探究活動分析[J].數學教學研究， 2016（8）：11.

責任編輯：顏瑩

Imagination： the Important Cornerstone for Promoting

Childrens Thinking Development

YAO Rui

（Xuzhou Minzhulu Primary School， Xuzhou 221000， China）

Abstract： Children are good at imagination and mathematics teachers may help children exercise their imagination in classroom teaching by means of accumulating materials through fertile imagination， analogical association to form skills， and learning by trial and error to construct fields. To lay a solid foundation for childrens creativity cultivation， teachers may utilize the development of imagination to enhance childrens development in their mathematical imagery thinking and abstract thinking.

Key words： imagination; creativity; thinking development