初中數學教學中數形結合思想的實踐研究

王少華

摘? 要：現如今教學體制不斷改革，對數學教學提出了更多的挑戰。因此，教師需將數形結合的方法應用于實際教學當中，這對于培養學生的個人能力提供了基礎要求。基于上述內容，本文重點探討了數形結合思想的運用策略，以期為數學教學提供參考建議。

關鍵詞：數形結合;數學思想;運用策略

引言：

在現階段的初中數學學習中，由于數學理論的抽象性特征難免會導致學生產生畏難情緒。因此，教師需將數形集合的方法融入數學教學中，將各類數學難題變得更為直觀，促使各類數學難題變得更為簡單。同時，教師需結合各類數學理論進行綜合性探索，創新數學教學方法，優化課堂氛圍，提高學生的主觀能動性。

一、數形結合思想概述分析

數形結合，顧名思義就是通過結合圖形、代數方面的理論，巧妙地將各類知識點進行綜合性總結，進而將抽象的數學概念、數學理論變得更為直觀。該方法運用過程中，強調了對學生數學建模能力的培養，幫助學生在圖形中認知各理論的基本含義，這對于提升學生的數學情感、數學價值觀、數學邏輯能力提供了良好的意境空間，進而緩解了學生數學學科方面的壓力。

二、基于初中數學教學的運用策略分析

（一）情境導入，培養學生的思維空間

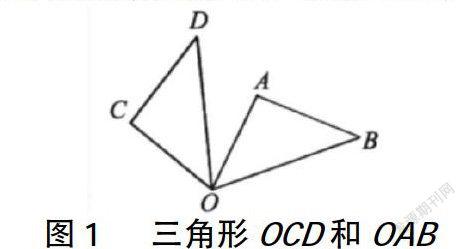
教師應結合合理的數學理論，運用相應的情境予以導入，充分展現數學教學的核心價值。在此過程中，教師應選取多媒體設備導入不同的圖形，權衡一個合理的度，突出章節的難點和重點，幫助學生快速步入學習氛圍當中。例如，在人教版《圖形的旋轉》的教學中，首先教師應向學生展示各類圖形的旋轉過程，如圖1所示，為三角形順時針旋轉某角度的三角形。

在此過程中，教師應引導學生觀察三角形是如何旋轉成三角形的，引導學生運用語言進行表述。此時，學生們通過討論，總結出了“我知道了影響圖形旋轉的三要素是旋轉中心、旋轉點以及旋轉角度。”值得注意的是，需引導學生注意這三個要素在旋轉過程中的變化情況，幫助學生快速掌握這方面的知識點，進而逐漸養成數形結合的基本思想。隨后，教師可借助以下例題進行問題引入，讓學生對該問題進行系統的思考。

例1：下列四個圖像中，分別以它們所在的圓的圓心作為旋轉中心，順時針旋轉120°后，能與原圖形完全重合的是？

分析：需分析各圖形的最小旋轉角度，結合旋轉角度判斷旋轉后的圖形是否與原圖形重合。

解析：圖形A的旋轉后能與原圖形重合的最小旋轉角度為：360°÷3=120°;圖形B最小旋轉角為360°÷4=90°;圖形C的最小旋轉角為360°÷2=180°;圖形D的最小旋轉角為360°÷5=72°。綜上分析可以得到，順時針旋轉120°后可得到與原圖形重合的圖形為A，故該題選A。

通過上述的例題，讓學生初步認知旋轉角的核心作用，有利于學生快速地掌握相關的基礎理論，這對于提升學生的學科素養有積極意義，也能讓學生在圖形中了解旋轉的定義，進而實現“數形結合”教學的目的。最后，教師應對旋轉的理論進行綜合性綜合，使用較為簡單的語言進行總結，保證所有學生都能全面理解這方面的理論。

（二）數形結合，培養學生的運算能力

在現階段的初中數學教學中，教師應引入數形結合的方法于代數方面的問題當中，有利于加快學生的數學運算效率。因此，教師應結合不同的數學例題，讓學生在這些例題中進行系統的分析，從而達到相應的教學目的。例如，在人教版《實數》的講解中，則可以引入數軸的模型，要求學生在數軸上表示相應的數字，結合數軸的方向判斷數據的大小，進而幫助學生更為直觀地了解實數的基本性質。此時，教師可以引入以下例題，讓學生進行綜合性的分析。

例2：已知實數在數軸上的位置如圖所示，那么，在、-、-、+中，最大的一個是？

分析：數軸中已經表示了、、三個數字的具體位置，應針對性地分析、、三者的大小，結合相應的運算即可達到求解目的。

解析：由于-1<<0;0<<<1，所以是負數且在-1和0之間，那么為整數且大于1，-是的相反數，那么-≈，由于>，那么-的值小于1，由于|-|≈||，所以+的值趨于0，所以該題可以得到最大。該題也可以直接賦值，利用賦值實際值進行比較，即設=、=、=，通過運算，也可以得出>1，也能快速得到相應的答案。

教師應對上述理論予以綜合性的總結，結合相應的視頻，讓學生系統地認知實數與數軸之間的位置關系，這對于提升學生的抽象思維能力、解題思維能力有積極的意義，進而達到核心教學的目的。最后，教師需講述數形結合方法在不等式題型解題的運用方法，將數軸與不等式向結合，讓學生牢記相關概念，這對于提升學生的數學學科能力有積極的意義。

三、結束語

綜上所述，將數形結合的方法運用于現階段的數學教學當中，結合不同的教學模式進行優化創新。同時，還應拓展相應的數學例題，幫助學生快速了解數形結合方法的運用模式，利于提升學生數學核心素養。

參考文獻：

[1] 林衛. 數形結合思想在初中數學教學中的實踐研究[J]. 數學學習與研究，2016（2）：36-36.

[2] 張旭華. 初中數學教學中滲透數形結合思想的研究[J]. 考試周刊（35）：65-65.