培養(yǎng)邏輯推理 提升數(shù)學(xué)運(yùn)算
——“數(shù)列求和”教學(xué)案例

張強(qiáng)

（內(nèi)蒙古巴彥淖爾市烏拉特中旗第一中學(xué)，內(nèi)蒙古巴彥淖爾 015300）

1 背景

數(shù)列作為高中數(shù)學(xué)的重要內(nèi)容，是歷屆高考的必考內(nèi)容。數(shù)列教學(xué)的核心素養(yǎng)——邏輯推理和數(shù)學(xué)運(yùn)算。借助我國先人之?dāng)?shù)學(xué)經(jīng)典展開教學(xué)，讓學(xué)生感受我國文明之璀璨，把握三維目標(biāo)，體現(xiàn)數(shù)學(xué)價(jià)值，呈現(xiàn)數(shù)學(xué)魅力。數(shù)列求和作為數(shù)列教學(xué)的重要模塊，是以兩個(gè)基本數(shù)列——等差數(shù)列和等比數(shù)列為基礎(chǔ)，進(jìn)一步提升邏輯推理和運(yùn)算能力，學(xué)會(huì)建立一般數(shù)學(xué)模型，強(qiáng)化實(shí)際問題的考察。在解決具體問題時(shí)，要熟練運(yùn)用分類討論、轉(zhuǎn)化歸納、類比推理等數(shù)學(xué)思想，將表象很難求和的問題轉(zhuǎn)化為我們熟悉的求和形式。本節(jié)課從公式法求和、分組求和、并項(xiàng)求和、裂項(xiàng)求和、錯(cuò)位求和五個(gè)角度，闡述數(shù)列求和的方法，遵循學(xué)生循序漸進(jìn)的認(rèn)知規(guī)律，讓學(xué)生在感知知識(shí)的同時(shí)，感受數(shù)學(xué)的樂趣。

2 教學(xué)設(shè)計(jì)

2.1 提出問題 畫龍點(diǎn)睛

教師：數(shù)列的基本就在于等差數(shù)列和等比數(shù)列，對于這兩種數(shù)列，我們怎樣求和，看下面的問題。

問題1：

⑴2+4+6+…+2n=

⑵1+2+2+2+…+2=

學(xué)生1：這兩個(gè)數(shù)列求和，直接用等差數(shù)列和等比數(shù)列的前n項(xiàng)和公式求解。答案是n(n+1),2-1

教師：有不同意見嗎？

學(xué)生2：第⑵題應(yīng)該有n+1項(xiàng)，答案是 2-1

方法點(diǎn)睛（教師）：同學(xué)們，利用公式法求和，一定要搞清首項(xiàng)、公差（公比）以及數(shù)列的項(xiàng)數(shù)。

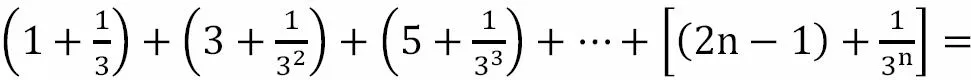
教師：請同學(xué)們認(rèn)真觀察，我們能否對該數(shù)列求和。

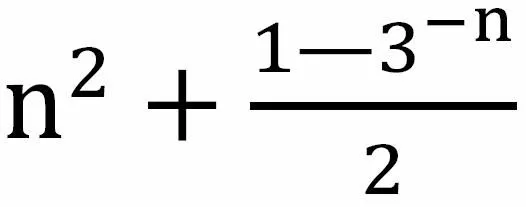
方法點(diǎn)睛（教師）：通過分組，得到等差或等比數(shù)列，分別求和再相加即可。這種方法叫做分組求和法。

問題3：S=1-2+3-4+…+(-1)·n，當(dāng)n為奇數(shù)時(shí)，S= ，當(dāng)n為偶數(shù)時(shí)，S=