思維可視化技術體現邏輯推理

李青

摘 要：文章借助思維可視化技術分析證明立體幾何中的垂直問題，將復雜的邏輯推理問題層層解析，感受思維可視化技術的優勢，并在這一過程中注重邏輯推理這一核心素養的培養.

關鍵詞：思維可視化;數學學科;核心素養;培育路徑

核心素養之一的“邏輯推理”，是指從一些事實和命題出發，依據邏輯規則推出一個命題的思維過程，主要包括兩類推理，一類是合情推理，包括歸納推理和類比推理，另一類是演繹推理。數學公式、定理、性質等結論的教學是新授課的主要內容，對于某些重點、難點結論的發現和證明，既符合新課標倡導的“讓學生體驗數學發現和創造的歷程”，也是培養學生邏輯推理能力的好素材。邏輯推理主要包括合情推理與演繹推理兩種推理形式，對于邏輯推理核心素養的生成關鍵在于培養學生清晰的、有條理的、合乎邏輯的理性思維品質。因此，可以借助高中數學中的代數證明與幾何證明來培養學生的演繹推理。

《新課標》強調，教師應當摒棄以枯燥授課與大量練習為主的教學模式，注重培養學生的數學思維與核心素養.邏輯推理作為高中數學六大核心素養之一，是學生得到數學結論、構建數學知識體系的重要方式。在本文中，筆者根據多年的教學實踐，以一道立體幾何的證明題為例，在思維可視化技術中呈現邏輯推理，簡單探討培養學生邏輯推理能力的具體策略，旨在發展學生的數學核心素養。

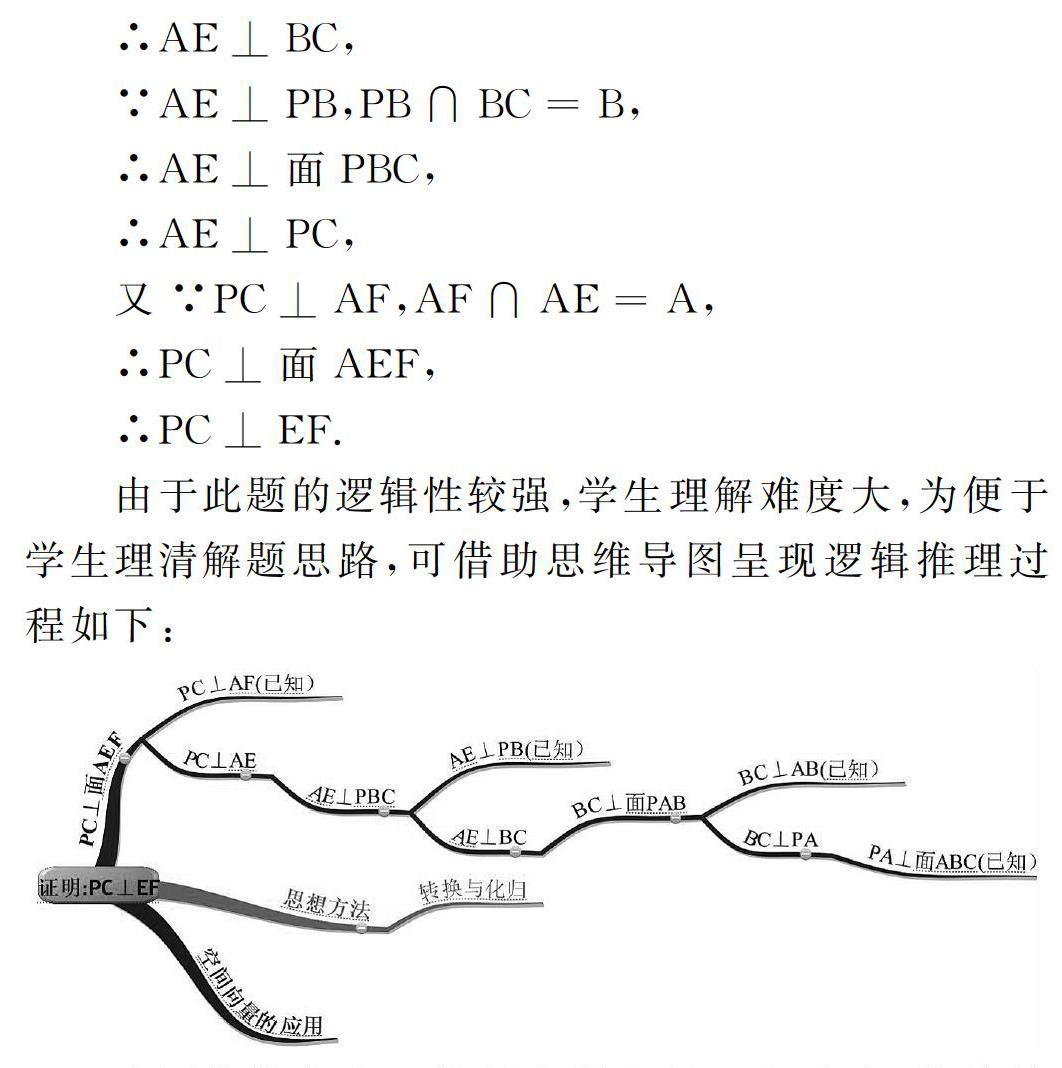
案例：如圖，PA⊥平面ABC，AE⊥PB，AB⊥BC，AF⊥PC，垂足分別為E、B、F求證：PC⊥EF;

由于此題的邏輯性較強，學生理解難度大，為便于學生理清解題思路，可借助思維導圖呈現邏輯推理過程如下：

本圖的優點在于能弱化學生的理解難度，將籠統的邏輯推理問題分步呈現，清楚每一步已有結論和待證明結論，讓學生的思維層層細化，順藤摸瓜，最終將每一步待證明結論回歸已知條件或公理、定理，進而問題得以解決。

在日常的教學活動中，廣大教師想必同筆者一樣，總是會遇到這樣一些情況： 平時對學生反復講解的一類問題，在考試中遇到同樣的問題時學生還是不知所措; 對舊問題稍加改編，學生就變得一頭霧水，經常是老師一講就會，學生一做就錯……出現這些問題的原因正是因為學生僅僅停留在了模仿照抄、機械學習的層面上，而缺少新認知與已有認知間的聯系.基于這一點考慮，我們借助思維可視化技術讓學生真正感悟數學的真諦，領會思維的過程，找到解決問題的路徑和方法，建立已知和未知知識間的聯系，最終達到有意義學習的目的.

參考文獻

[1]張艷.基于邏輯推理數學核心素養培養模式的嘗試——以“對棱相等四面體的由來”為例[J].中學教研（ 數學），2018.

[2]明永學.培養邏輯推理能力 發展數學核心素養[J].高中數學教與學，2018.