不回避 不懼怕
——高中物理關于微積分的教與學
王 娟
(江蘇省淮安市淮陰中學 223002)
一、物理課堂內外關于微積分教與學的現狀
1.教材編寫者回避
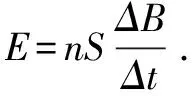
2.高考命題者回避
近幾年出現了大量的可以利用微積分來解決問題的高考題和高考模擬題,但是在具有指揮棒作用的高考試卷的參考答案中我們卻沒有看到利用微積分這種簡單方法來求解的答案,而更多的是利用微元求和的思想來處理,這對中學物理微積分的教學也起到一定的阻礙作用,因此教師在課堂上不太愿意也不太敢用微積分的方法去解決問題.
3.學生關于微積分的學習是霧里看花
對于微積分初步知識的學習,數學和物理都有所涉及,但都沒有做出具體的要求,學生所能達到的程度僅限于一知半解,因此在應用微積分知識去解決物理問題時只能是霧里看花.
二、現行中學階段微積分教學有效策略的研究
1.教學時間安排
在高一,物理必修1和必修2中出現了15處體現微積分思想的內容,到了高二,學生在數學教材中系統的學習了微積分的初步知識,但這兩者在很多學生的頭腦里還是兩條平行線,還不能做到將數理進行整合與優化.到了高三物理第一輪復習前我們可以將這兩者進行有機的整合,適度地應用微積分,深化已學過的物理概念,拓展解題思路,優化解題過程.
2.理解并熟記常用的求導和積分公式
(1)常用的求導公式
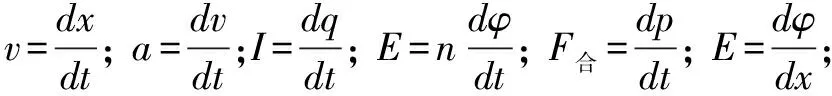
(2)常用的積分公式
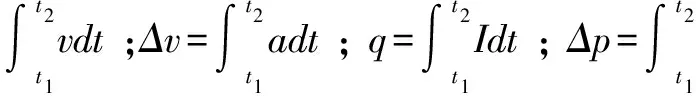
三、利用微積分知識處理高中物理問題實例分析
1.求導方法的應用實例
導數在物理里的應用實質上是將物理內容結合到它的幾何意義中.導數在求解切線斜率和極值時具有比較簡單方便等優勢,因此以后碰到這類問題時,我們可以試著用導數來解決.
(1)利用導數結合物理圖象對物理量的變化進行判斷
例題真空中有一半徑為r0的帶電金屬球殼,通過其球心的一直線上各點的電勢φ分布如圖1所示,r表示該直線上某點到球心的距離,r1、r2分別是該直線上A、B兩點離球心的距離.下列關于A、B兩點電場強度大小判斷正確的是(A).

圖1
A.EA>EB
B.EA=EB
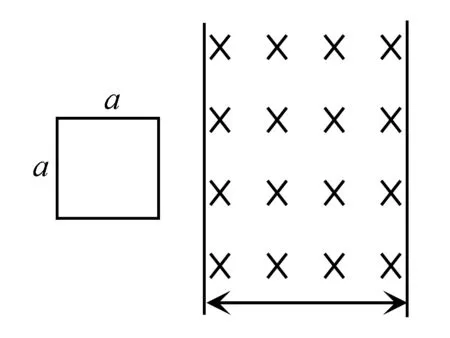
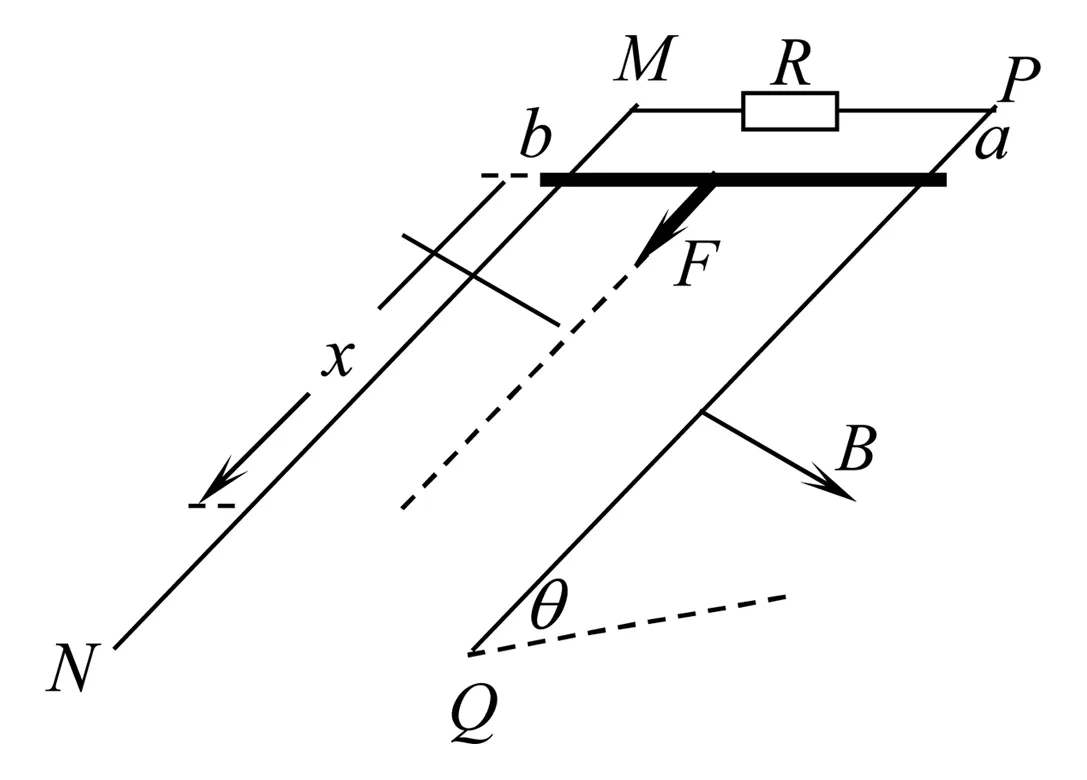
C.EA D.不確定 強度的大小. (2)利用導數結合數學方法求解物理量的極值 例如求某一物體在運動過程中加速度的最大值,其加速度的表達式為: 發現加速度是一個關于θ的函數,令f(θ)=sinθ-sin3θ 令f′(θ)=0,即cosθ-3sin2θcosθ=0 2.積分方法的應用實例 積分在高中物理中的應用分為兩類,一類是直接利用物理意義積分,另一類是利用數學方法積分. (1)直接利用物理意義積分 圖2 例題如圖2所示,在光滑的水平面上,有一垂直向下的勻強磁場分布在寬為L的區域內,有一個邊長為a(a (2)利用數學方法積分 圖3 例題如圖3所示,兩根足夠長的光滑直金屬導軌MN、PQ平行固定在傾角θ=37°的絕緣斜面上,兩導軌間距L=1m,導軌的電阻可忽略.M、P兩點間接有阻值為R的電阻.一根質量m=1kg、電阻r=0.2Ω的均勻直金屬桿ab放在兩導軌上,與導軌垂直且接觸良好.整套裝置處于磁感應強度B=0.5T的勻強磁場中,磁場方向垂直斜面向下.自圖示位置起,桿ab受到大小為F=0.5v+2(式中v為桿ab運動的速度,力F的單位為N)、方向平行導軌沿斜面向下的拉力作用,由靜止開始運動,測得通過電阻R的電流隨時間均勻增大.g取10m/s2. ①試判斷金屬桿ab在勻強磁場中做何種運動,并請寫出推理過程; ②求電阻的阻值R; ③求金屬桿ab自靜止開始下滑通過位移x=1m所需的時間t和該過程中整個回路產生的焦耳熱Q. 在t=0.5s內產生的焦耳熱 “應用數學處理物理問題的能力”是物理學科高考考試說明中的五條能力要求之一.高考物理試題的解答離不開數學知識和方法的應用,以物理題為載體滲透考查數學能力是高考命題的永恒主題.在現行數學教材已經加入了微積分知識的情況下物理教育者不要回避這一問題,要能夠做到與時俱進,在原有學科教學的基礎上向前邁出小小的一步,以期學生對高中物理知識能夠產生豁然開朗的感覺,因為只有教師做到真正的不回避學生才能做到真正的不懼怕.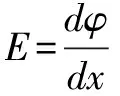

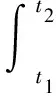
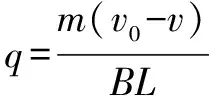
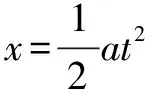
四、微積分知識教學感悟

