基于發展學生數學核心素養目標的基本不等式的備考策略

張麗麗

(江蘇省南京市第五高級中學 210000)

在高中教學過程中，教師會重點強調基本不等式解題步驟為“一正、二定、三相等”，但是在實際解題中學生會犯錯誤，這就容易在整個過程中丟失分數.在此背景下，如何引導高中生把握基本不等式的本質，搞清楚解題技巧，如何提升他們的數學核心素養，從而在做題過程中不丟分甚至少丟分就變得非常重要.

一、注重基礎，穩拿分數

數學知識來源于日常生活，但是經過數學家抽象化、符號化后的內容變得抽象、難以理解，這就很難深入開展高中數學教學.在教學過程中，廣大數學教師不妨把基本不等式與其幾何意義進行連接，使學生了解和掌握它的成立條件，從而對知識進行外延，加深他們對基本不等式相關知識的理解.一般而言，湊項法是基礎的基礎，教師要引導學生在拿到題目后觀察不等式，將其配湊(湊項、湊系數等)成符合其條件.

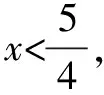
解析第一步，根據觀察已知函數的表達式，通常不符合基本不等式成立的三個條件“一正二定三相等”，將其配湊(湊項、湊系數等)成符合其條件.

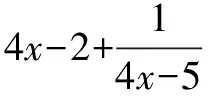
第二步，使用基本不等式對其進行求解即可.

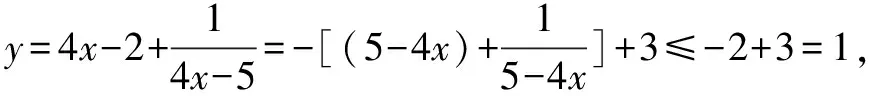
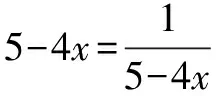
第三步，得出結論.

故當x=1時，ymax=1.

點評本題需要調整項的符號，又要配湊項的系數，使其積為定值.

二、適度拔高，熟練應用

在高考試卷中，絕大多數的數學試題屬于中等難度試題，教師在學生掌握基礎知識之上進行適度拔高很有必要.在教學過程中，教師要精選一些數學試題，通過精講、精煉來達到適度拔高和拓展目的，從而確保高中生在考試中不丟分數，拿到大多數的分數.最值問題涉及到基本不等式的求解，學生要觀察函數的表達式特征，將其分子或分母一次形式視為一個整體來進行湊項.

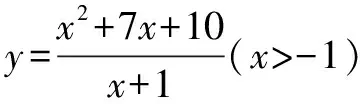
解析第一步，首先觀察已知函數式特征，如分子(或分母)是二次形式且分母(或分子)是一次形式.

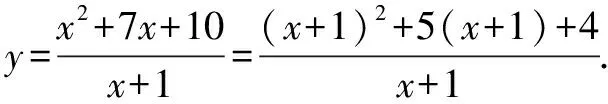
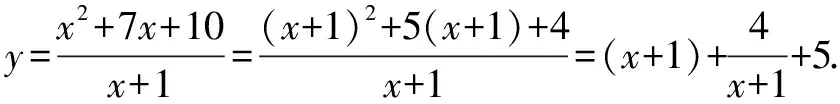
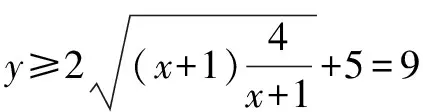
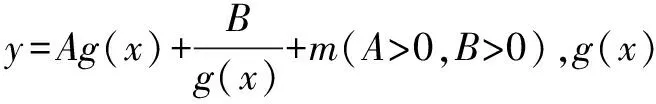
通過中等難度試題的練習，學生能夠了解高考考查難度，增強應對高考的信心.

三、克服難題，綜合運用

在很多高考試卷中，基本不等式會和其它知識點進行有機結合作為大題甚至是壓軸題出現，這大大提升了試題的難度.對于此類問題，教師在教學中不能放棄，要引導學生進行綜合分析，找到試題關聯的知識點，對問題進行剖析找到本質，從而提升解決問題的綜合能力.在日常訓練中，學生經常會遇到函數與基本不等式結合求值域的問題，此時，在湊項、應用不等式的基礎上還要結合函數單調性來進行求解，此類問題難度較大.

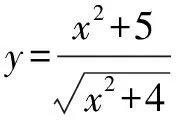
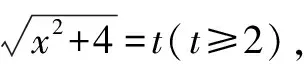
第二步，運用基本不等式并檢驗其等號成立的條件，若等號取不到則進行第三步，否則，直接得出結果即可：

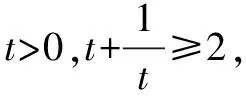
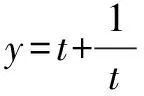
第四步，得出結論.

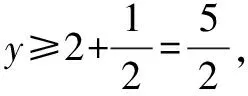
針對難度較大的試題，教師要引導學生深入探究，采取多個角度進行分析，找到問題背后的知識點，學會應用知識尋找問題的切入點.

總之，基本不等式在高中數學教學中占據非常重要的地位，也是學生學習的難點和重點，教師要幫助他們在理解和掌握的基礎上靈活運用相關知識，把握內在的數學本質，最終為學習其它數學知識點來打下堅實的基礎，也為獲取高考的高分增添一份保障.