如何培養(yǎng)學(xué)生高中數(shù)學(xué)直觀想象能力

黃旭明

(福建省福安市第三中學(xué) 355002)

直觀的本質(zhì)就是在直接接觸客觀事物的過程中所產(chǎn)生的感性認(rèn)識(shí)，而想象的本質(zhì)是在人類大腦之中對已經(jīng)存在的表象予以加工而產(chǎn)生了一種新形象的一種心理過程.數(shù)學(xué)直觀想象力就是在幾何直觀與空間想象當(dāng)中，去對事物的變化和基本形態(tài)進(jìn)行感知，最后通過對圖形的理解來解決一些數(shù)學(xué)問題.它是數(shù)學(xué)核心素養(yǎng)的重要組成部分之一，在數(shù)學(xué)教學(xué)當(dāng)中直觀想象有三種基本表現(xiàn)形式，即利用圖形構(gòu)建直觀模型、運(yùn)用圖形理解數(shù)學(xué)問題、利用圖形解決數(shù)學(xué)問題.能夠看出來，不論是哪一種表現(xiàn)形式都無法脫離圖形而存在，因此這就需要教師在教學(xué)的過程中加大對學(xué)生作圖與識(shí)圖能力的培養(yǎng).

一、通過數(shù)形聯(lián)系，培養(yǎng)圖形運(yùn)用能力

直觀想象的本質(zhì)就是通過對圖形進(jìn)行理解，以此來解決一些數(shù)學(xué)問題.在高中數(shù)學(xué)之中，數(shù)與形之間有著密不可分的聯(lián)系，將這兩者的聯(lián)系建立起來，可以有效促進(jìn)學(xué)生對問題的認(rèn)知與理解，進(jìn)而快速尋找到解決問題的方式.“數(shù)缺形少直觀，形缺數(shù)難入微.”通過數(shù)形結(jié)合的方式解決數(shù)學(xué)問題，不但要讓學(xué)生將原本抽象的題目直觀化，還應(yīng)該要加大對學(xué)生圖形洞察力的培養(yǎng)，使其可以依照圖形之中的已知信息對結(jié)論進(jìn)行直觀推理，然后獲得解題思路，提升直觀想象核心素養(yǎng).

在高中數(shù)學(xué)之中向量一直以來都是非常重要的一項(xiàng)考察點(diǎn)，它不僅具有代數(shù)的抽象性和嚴(yán)謹(jǐn)性，同時(shí)還具備幾何的直觀性.因此在各大考試過程中都尤為重視學(xué)生對向量運(yùn)算法則的掌握情況和對幾何意義的理解.如果在教授向量的時(shí)候，可以引導(dǎo)大家先將向量的本質(zhì)認(rèn)識(shí)清楚，并學(xué)會(huì)運(yùn)用圖形去解決一些問題，除了可以縮減學(xué)生解題的時(shí)間之外，還能夠培養(yǎng)起來學(xué)生的直觀想象力，進(jìn)而提升大家運(yùn)用圖形的能力.

例1 已知|a|=|b|=1,a·b=0,且|c-a-b|=1,那么|c|的最大值為____.

解析由于向量本身就是數(shù)形相互結(jié)合發(fā)展出來的，那么在解決這類問題的時(shí)候就需要將向量加減法的基本幾何意義把握住，然后再通過圖形，將向量幾何的直觀性完全呈現(xiàn)出來，以此來有效解決問題.

對于這一道例題來說，在解答的時(shí)候就可以依照這一思路進(jìn)行.具體：

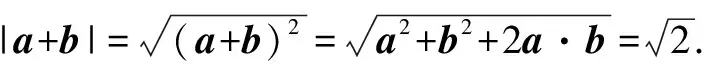
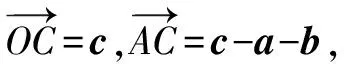
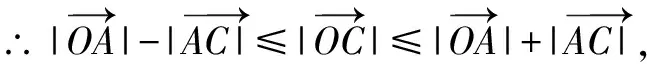
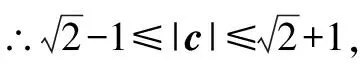
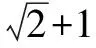
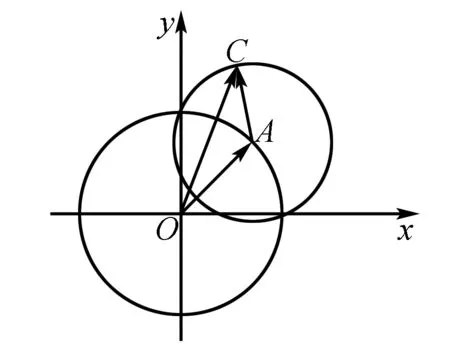
圖1

通過這一例題分析之后能夠讓學(xué)生對向量加法與減法存在的幾何意義有更深一步的理解，并且還可以讓大家能夠感受到通過對圖形的認(rèn)識(shí)便能夠快速解決一些數(shù)學(xué)問題，進(jìn)而有利于培養(yǎng)大家的直觀想象力，從而提升圖形運(yùn)用的能力.

二、通過模型，培養(yǎng)空間思維

教師在教學(xué)的時(shí)候還需要重點(diǎn)引導(dǎo)大家通過構(gòu)造直觀模型解決一些數(shù)學(xué)問題，一般構(gòu)造的直觀模型主要包含有立體幾何、解析幾何以及平面幾何.在立體幾何當(dāng)中主要包含有四面體及長方體等等；在解析幾何模型之中主要是點(diǎn)與線之間的距離、點(diǎn)與點(diǎn)之間的距離、圓錐曲線、斜率等等；在平面幾何之中主要包含有三角形、圓等.這種直接將數(shù)學(xué)問題直觀化的模式能夠促進(jìn)對問題的推理及把握，進(jìn)而簡化數(shù)學(xué)問題.這也是目前培養(yǎng)直觀想象核心素養(yǎng)最有效的一項(xiàng)途徑.

比如，在高中數(shù)學(xué)教材當(dāng)中，立體幾何與幾何模型的制作有著極為密切的聯(lián)系，所以在教授這節(jié)內(nèi)容的時(shí)候就需要引導(dǎo)學(xué)生們加強(qiáng)對模型的觀察，并讓大家在制作模型的過程中加強(qiáng)對數(shù)學(xué)問題的思考.在解答立體幾何的過程中，可以將一些特殊模型運(yùn)用進(jìn)去，例如長方體或者正方體等，就可以讓大家直觀感受到這些模型之中點(diǎn)線面所存在的基本位置關(guān)系，從而就可以積累出來立體幾何的表象，提升對立體圖形的直觀感，最后養(yǎng)成空間思維的基本能力，這對于培養(yǎng)學(xué)生直觀想象力同樣也具備一定的積極意義.

例2 (見2014年全國卷)如圖2，網(wǎng)格紙上小正方形的邊長為1，粗實(shí)線畫出的是某多面體的三視圖，則該多面體的各條棱中，最長的棱的長度為( ).

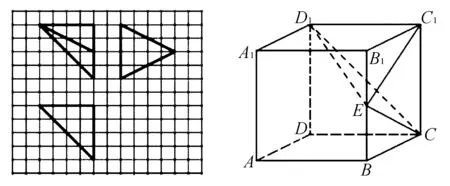
圖2

通過對這一例題的基本解讀能夠發(fā)現(xiàn)，它主要是要求學(xué)生將三視圖還原成為一個(gè)幾何體，然后在其中找到最長的棱.這類題目在各大考試當(dāng)中非常常見，通常會(huì)對學(xué)生的想象力和空間思維能力提出較高的要求，因此大部分人都不會(huì)做.如果在教學(xué)的時(shí)候，將特殊模型運(yùn)用進(jìn)去，讓學(xué)生將模型的正、俯、側(cè)三個(gè)視圖分別當(dāng)作幾何體在模型之中里、底與右側(cè)三面的投影，就可以有效增強(qiáng)題目的直觀性，進(jìn)而激發(fā)學(xué)生的空間想象力.以后學(xué)生在遇到類似題目無法有效還原的時(shí)候，還可以讓大家在特殊模型之中將幾何體的頂點(diǎn)確定出來，最終將幾何體還原出來.

就例2來講，就可以完全選擇一個(gè)棱長是4的正方體，從其俯視圖當(dāng)中就可以得知，其頂點(diǎn)是不會(huì)出現(xiàn)在A點(diǎn)和A1點(diǎn)的，也就是可以直接將這兩個(gè)頂點(diǎn)排除掉，借用相同的理由在正視圖當(dāng)中還能夠再將A點(diǎn)與D點(diǎn)排除掉；又在側(cè)視圖當(dāng)中將B點(diǎn)與B1點(diǎn)排除掉，那么剩下的三個(gè)頂點(diǎn)就會(huì)成為幾何體的頂點(diǎn)，接下來再依照正視圖就能夠?qū)⑷忮F的第四個(gè)頂點(diǎn)確定出來，即棱BB1的中點(diǎn)E.所以最后的幾何體就是E-CC1D1，最長的一條棱就是ED1,其長度為6.

在培養(yǎng)學(xué)生直觀想象力的過程中，運(yùn)用空間幾何體的三視圖可以起到事半功倍的效果，并且在特殊模型的作用下，還可以有效提升大家的直觀感受，并給想象力的發(fā)揮創(chuàng)設(shè)更廣闊的空間，進(jìn)而整個(gè)解題過程變得更加迅速和便捷，最后提升學(xué)生的直觀想象力.

三、通過圖象特征理解，培養(yǎng)數(shù)形結(jié)合

在高中數(shù)學(xué)學(xué)習(xí)過程之中函數(shù)是非常關(guān)鍵的一項(xiàng)研究對象，其圖象基本的幾何特征可以將函數(shù)的基本性質(zhì)有效展現(xiàn)出來，另外借助于圖象還能夠迅速找到解決問題的方式.在培養(yǎng)直觀想象力的過程中直觀洞察力是非常顯著的一項(xiàng)特征，它的本質(zhì)就是人類在獲得既定情境圖象的基本信息之后，可以將這些信息和自己已經(jīng)具備的知識(shí)體系相互聯(lián)系起來，并從中將解決問題的能力篩選出來.所以能夠發(fā)現(xiàn)，讓學(xué)生將基本初等函數(shù)的基本圖象特點(diǎn)和一些較為常見的圖形變換掌握并完全理解，可以有效促進(jìn)在解題方面的洞察力，最終提升直觀想象力，與此同時(shí)運(yùn)用得當(dāng)還能夠反過來促使數(shù)形結(jié)合能力得以提升.

例3 若函數(shù)f(x)的定義域是R，其圖象關(guān)于原點(diǎn)對稱，當(dāng)x>0時(shí),f(x)=x3-2，那么函數(shù)f(x+2)全部的零點(diǎn)和是( ).

通過對上述例題的初步分析能夠發(fā)現(xiàn)，這重點(diǎn)是考察求函數(shù)圖象的基本性質(zhì)，其中f(x)是奇函數(shù)，所以這就能夠發(fā)現(xiàn)，當(dāng)x>0的話，那么其函數(shù)f(x)的解析式就能夠輕易得到，同理f(x+2)的解析式也能夠獲得，最后就可以將所有零點(diǎn)的和解出來.但是這道題目如果使用這種方式直接進(jìn)行解答的話，那么整體計(jì)算量相對就會(huì)比較大，所以這就可以將其奇偶函數(shù)的基本性質(zhì)結(jié)合進(jìn)去，站在函數(shù)圖象變換的角度上來解答這一例題就能夠迅速得到答案.

解析由題目可以得知f(x)是奇函數(shù)，當(dāng)其x>0的時(shí)候，f(x)=x3-2.

通過圖象可以獲得(圖3)，f(x)存在一個(gè)大于0的零點(diǎn)，即x1(x1>0)；再從其奇函數(shù)的基本性質(zhì)能夠得到，f(x)存在一個(gè)小于0的零點(diǎn)，即x2(x2<0)，并且這兩個(gè)零點(diǎn)都是關(guān)于原點(diǎn)對稱的，再從其函數(shù)性質(zhì)能夠獲得f(0)=0，也就是其函數(shù)零點(diǎn)x3=0.

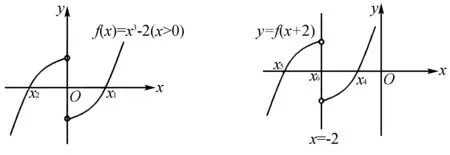
圖3 圖4

將其f(x)的圖象向左面平移兩個(gè)單位就可以獲得f(x+2)的圖象(圖4)，將其f(x)的零點(diǎn)向左面平移兩個(gè)單位可以獲得f(x+2)的零點(diǎn)，并且其零點(diǎn)x4與x5是關(guān)于(-2,0)對稱的，而x6=-2，所以最終就能夠獲得f(x+2)的全部零點(diǎn)和就是-6.

在解決上述的例題的時(shí)候，將學(xué)生比較熟悉的圖象平移變換以及對稱等相應(yīng)的知識(shí)內(nèi)容應(yīng)用進(jìn)去，就可以及時(shí)獲得題目之中的一些特定信息，由此就可以再依照直觀洞察力直接獲得最終題目的答案.總結(jié)來說，圖象的基本特點(diǎn)和變換是培養(yǎng)直觀洞察力的重要基礎(chǔ)，教師在上課的時(shí)候除了要讓大家可以精準(zhǔn)地觀察并繪制圖形之外，還要讓大家盡量掌握函數(shù)之中圖象的基本變換情況，這樣一來不但可以提升學(xué)生的直觀洞察能力，培養(yǎng)直觀想象力，還能夠反過來促進(jìn)數(shù)形結(jié)合能力的提升.

總的來說，在教學(xué)的時(shí)候培養(yǎng)大家的直觀想象力其本質(zhì)就在于培養(yǎng)大家通過數(shù)學(xué)視角去觀察和理解世界，并通過相應(yīng)的方式，以圖形、模型和圖象為載體，促進(jìn)學(xué)生運(yùn)用圖形能力的提升，并進(jìn)一步培養(yǎng)基本的空間想象力.這樣一來不但能夠直接簡化一些數(shù)學(xué)問題，還能夠促進(jìn)大家創(chuàng)新思維的提升，進(jìn)而發(fā)展起來基本的直觀核心素養(yǎng).