借助輔助圓 搭建動態(tài)最值問題求解橋梁

周志韌

(上海市同濟大學(xué)附屬實驗中學(xué) 201805)

初中數(shù)學(xué)中的很多幾何問題，看似與圓沒有任何關(guān)系，但是借助已知條件恰當(dāng)構(gòu)建輔助圓，常常可以實現(xiàn)問題的簡單化和簡潔化，讓解題思路豁然開朗.究竟如何發(fā)現(xiàn)圓、何時構(gòu)建圓是關(guān)鍵問題，本文就結(jié)合例子詳細講解.

一、借助圓的定義，構(gòu)建輔助圓

圓的定義告訴我們，圓心到圓上任意一點的距離都相等或者是到圓心距離都相等的點在圓上.當(dāng)問題中涉及運動過程，涉及到某一定點且某一線段的長度保持不變時，可以嘗試構(gòu)建圓，借助圓的性質(zhì)進行求解，如：

圖1

例1如圖1，已知△ABC是直角三角形，∠C=90°,AC=6,BC=8，邊AC上有一點F，滿足CF=2，邊BC上有一動點E，現(xiàn)將△CEF沿著直線EF進行翻轉(zhuǎn)，使得點C落在P，則點P到邊AB最小距離是( ).

反思借助已知條件將點到邊的距離轉(zhuǎn)化為圓上某點到某邊最短的距離，實現(xiàn)了原問題的轉(zhuǎn)化，實現(xiàn)原問題的難度降低.轉(zhuǎn)化的關(guān)鍵在于能夠準(zhǔn)確把握已知條件實現(xiàn)知識的遷移和轉(zhuǎn)化.

二、借助圓切線尋找相關(guān)量的關(guān)系，構(gòu)建輔助圓

結(jié)合圓的切線和三角函數(shù)的關(guān)系，可以知道圓O外一定點A，與圓外一動點P，當(dāng)AP與圓相切時，∠PAO取得最大值.借助此特性，可以解決某類最值問題，如：

圖2

例2如圖2，點A(2,0),B(0,2)，圓C是半徑為1，圓心坐標(biāo)(-1，0)的圓.D是圓C上的動點，線段DA與y軸的交點是E，求△ABE面積最小值.

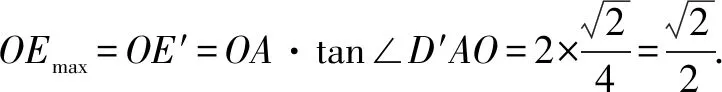
反思此題關(guān)鍵在于能夠用恰當(dāng)?shù)氖阶雍线m表示S△ABE，并借助題意構(gòu)建以線段AC為直徑的輔助圓.

三、利用動點與定線段構(gòu)成張角是定值，構(gòu)建輔助圓

在同一個平面內(nèi)，一動點C是已知直線AB外的一個點，且∠ACB為一定值，那么點C在以線段AB為弦長的某圓弧上；當(dāng)∠ACB=90°特殊角時，點C在以AB為直徑的圓上.熟悉此類動點與定線段所構(gòu)成的角為定值的情形，明確此動點是在以定長線段為弦的圓上運動，特別是出現(xiàn)90°時，要高度留意90°的圓周角對應(yīng)的那條弦實際就是直徑的的特殊情況，是解決以此模型為基礎(chǔ)的動點構(gòu)成的最值問題.

圖3

例3如圖3，邊長是4的正方形ABCD對角線是BD，一異于端點B,D的點P在BD上運動，連接AP，并過點B作垂直于AP的垂線，垂足記為H，連接DH，則線段DH的位于( )時(位置)取值最小，最小值是( ).

反思此題模型關(guān)鍵在于找出定角、以及定角相對相應(yīng)的定線段；模型的運用離不開學(xué)生們已有的模型認(rèn)識，也離不開需要充分挖掘題目隱含的信息，借助挖掘的條件快速鎖定合適模型，然后依托模型的內(nèi)容幫助學(xué)生們快速解題.因此，積累特定情況所對應(yīng)的特殊模型結(jié)構(gòu)是十分有必要的.

幾何中最值問題，不僅要重視常見的幾何法、代數(shù)法等基礎(chǔ)方法，也要重視將“直”化“曲”，重視圓的知識的運用，熟悉常見的構(gòu)圓情景，把握情景中的本質(zhì)，通過構(gòu)建合適的輔助圓，促進問題的轉(zhuǎn)化與解決.