初中數(shù)學數(shù)形結(jié)合的應(yīng)用價值探討

沈麗蓉

(江蘇省海門中學附屬學校 226100)

在初中數(shù)學教學中，相較于教師將知識灌輸給學生，學習思想的滲透更有價值，數(shù)形結(jié)合便可實現(xiàn)該目標.因此，必須加強初中數(shù)學數(shù)形結(jié)合應(yīng)用價值的探究.

一、促進初中生形成全面、詳細的數(shù)學概念

在數(shù)學學習過程中，數(shù)學概念占據(jù)著舉足輕重的地位，是其邏輯的起始點，同時在數(shù)學教學中占據(jù)核心和基礎(chǔ)位置.不過，初中數(shù)學課本中所包含的數(shù)學概念，往往都對其進行高度概括，具有較強抽象性，增大學生記憶和應(yīng)用等的難度.數(shù)學教師在教學過程中，若是所應(yīng)用的教學方法為數(shù)形結(jié)合，必定能夠真正闡釋數(shù)學概念.

1.便于學生記憶和理解數(shù)學概念

將數(shù)形結(jié)合應(yīng)用于實際教學中，能有效轉(zhuǎn)變抽象概念，使其成為更為形象與具體的概念，為學生的記憶和理解提供相應(yīng)幫助，進而從根本上了解和認知數(shù)學概念，最終達到接受這一要求.例如說數(shù)軸，教師在進入課堂教學前可以準備好相關(guān)工具，包括標尺與稱桿等，方便學生在教學中明確這些工具都有三項特點，一是度量起點，二是單位，三是增減方向.通過發(fā)揮這三項特征的啟發(fā)作用，教師將數(shù)軸思想傳遞給學生.針對數(shù)軸思想而言，將其度量起點當作直線原點，度量刻度等同直線刻度，增減方向便是直線方向.數(shù)形結(jié)合勢必發(fā)揮重要作用，積極轉(zhuǎn)變初中生的數(shù)學概念學習過程，從具體模型轉(zhuǎn)變?yōu)檎嬲私夂驼莆粘橄蟾拍?

2.可實現(xiàn)學生數(shù)學認知結(jié)構(gòu)的優(yōu)化

針對數(shù)學認知結(jié)構(gòu)而言，以多種數(shù)學概念為對象，在學生的思維中實現(xiàn)內(nèi)化，進而構(gòu)建起數(shù)學思維結(jié)構(gòu)，更加具體來講，主要是指，在學生的思維中，所形成的數(shù)學概念、定理和解題法相互間的關(guān)系.對于數(shù)學這門學科，學生學習能力有其具體體現(xiàn)，也就是數(shù)學認知結(jié)構(gòu)，利用數(shù)形結(jié)合這一方法能夠強化概念與定理等的聯(lián)系及轉(zhuǎn)化，由此達到數(shù)學認知結(jié)構(gòu)優(yōu)化的目的.比如初中數(shù)學中的一元二次不等式，可通過已學的一元二次方程及二次函數(shù)圖象對其進行講解.在教學過程中，教師應(yīng)該使學生明確三者之間的關(guān)系，進而提高學生理解與認知一元二次不等式的深度，實現(xiàn)優(yōu)化數(shù)學知識結(jié)構(gòu)的目的.

二、增強學生數(shù)學解題能力

1.可幫學生發(fā)現(xiàn)最佳解題途徑

數(shù)形結(jié)合著眼于學生思維，在解題過程中，學生利用這一方法能夠轉(zhuǎn)換數(shù)字符號，使其成為圖象，由此發(fā)現(xiàn)最佳解題途徑.比如，通過應(yīng)用函數(shù)圖象解答最值問題.

a和b都是實數(shù)，并且a2+b2-4a+6b+11=0，求a2+b2的最大值和最小值.

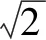
2.可幫助學生簡化和縮短思維鏈條

在題目求解中，學生都會在腦海中形成一條思維鏈，來源于他們對數(shù)學知識的優(yōu)化與整理.具有較強解題能力的學生，其思維鏈較為短少，而具有較弱能力的學生，其思維鏈比較長多，所以利用數(shù)形結(jié)合可簡化和縮短思維鏈，增強學生的解題能力.

舉例來說，在解答幾何問題時，若是直線不過圓心，但和圓在AB點相交，此時學生便能形成這一想法，即OA、OC與AC可組成直角三角形，也就是半徑與弦心距以及半弦長這三者組成直角三角形，可表示為OA2=AC2+AC2，由此可見，對于圓中的多項問題，通過這一知識模塊能將其簡化，進而增強學生解題能力.

三、強化學生數(shù)學思維能力

1.幫助學生形成形象思維

就形象思維而言，依賴于文字符號，由此形成直觀的數(shù)學表象，該思維最為突出的特點是必須憑借形象的直觀數(shù)學文字符號.利用數(shù)形結(jié)合能夠在很大程度上增多學生所掌握的數(shù)學文字符號，進一步發(fā)展他們的數(shù)學形象思維.

例如，當開展反比例函數(shù)教學時，某道題為：y=k/x，且k是除零以外的常數(shù).這一函數(shù)便是反比例函數(shù)，若是自變量是x，函數(shù)是y，通過函數(shù)圖象的分析能夠發(fā)現(xiàn)：其一，函數(shù)圖象屬于雙曲線；其二，如果k大于0，那么雙曲線所處的位置是第一象限和第三象限，并且在各象限內(nèi)x增大的同時y會減小；其三，如果k小于0，那么雙曲線所處的位置是第二象限和第四象限，并且在各象限內(nèi)x增大的同時y也會增大.經(jīng)由分析可提高學生認知與記憶這三點的深度，印刻在他們的思維中，勢必會使學生轉(zhuǎn)換該公式的數(shù)學符號，變成形象思維，進一步深化學生對反比例函數(shù)的認知.

2.可培養(yǎng)學生發(fā)散思維

在數(shù)學這門學科中，發(fā)散思維主要以同一問題或者是知識點為對象，在分析和研究中，產(chǎn)生各種思路與方法，由此構(gòu)建起一個思維過程，其終極目標便是探究和發(fā)現(xiàn)未知事物，掌握各種解題思路與方法.當開展數(shù)學教學時，利用數(shù)形結(jié)合能夠從不同角度設(shè)定并提問同一數(shù)學問題，進而對學生發(fā)揮啟發(fā)作用，激發(fā)他們新的不同類型的解題思維，實現(xiàn)增強學習能力的目的.比如直線與圓的位置關(guān)系，學生在判定過程中，通常會對比半徑與圓心至直線的距離.不過教師應(yīng)指出，同樣可以應(yīng)用圓和直線相交的點數(shù)，這一方法具有較高復雜度，不過仍舊從一個全新的角度判定了直線和圓的位置關(guān)系，以此激發(fā)學生發(fā)散思維.

在初中數(shù)學將教學中，數(shù)形結(jié)合的應(yīng)用率較高，本文只是簡單分析了該方法在初中數(shù)學中的應(yīng)用價值，還有待加強各方面的探究.總而言之，數(shù)形結(jié)合這一教學法如果可以發(fā)展成具有較強系統(tǒng)性的數(shù)學教學模式，勢必可以提高教學效率和質(zhì)量，強化教學效果.