運用一題多解提升學生數學綜合能力

涂友利

(福建省晉江市磁灶中學 362214)

一題多解能提升學生的數學建模能力、分析能力、獨立解決數學問題能力及思考內驅力等數學綜合能力，下面舉例說明．

實例1平行四邊形判定問題從同旁同角、構造內錯角、同位角及全等角度思考．

題目如圖1，在四邊形ABCD中，AB∥CD，∠B=∠D，求證:四邊形ABCD是平行四邊形．

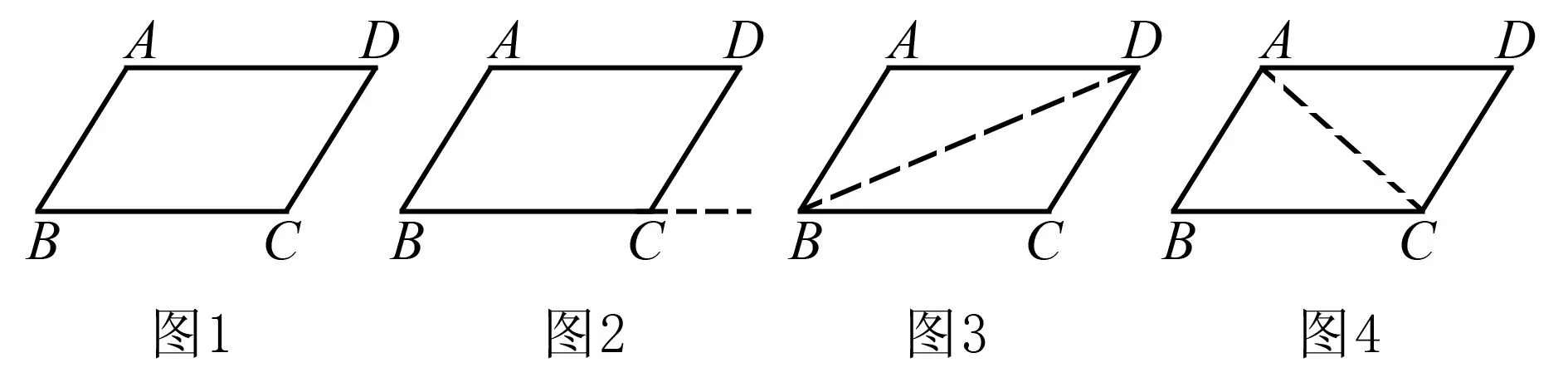
分析條件有一組對邊平行，與邊相關的判定方法只有三種:兩組對邊分別平行、兩組對邊分別相等及一組對邊平行且相等，為了描述方便，記為判定1、2、3．

解法1∵AB∥CD，∴∠B+∠C=180°.∵∠B=∠D，∴∠D+∠C=180°，∴AD∥BC，∴四邊形ABCD是平行四邊形．

解法2如圖2，延長BC至E.∵AB∥CD，∴∠B=∠DCE.∵∠B=∠D，∴∠D=∠DCE，∴AD∥BC，原證成立．

解法3如圖3，連結BD.∵AB∥CD，∴∠ABD=∠CDB.∵∠B=∠D，∴∠ADB=∠CBD，∴AD∥BC，原證成立．

解法4如圖4，連結AC， ∵AB∥CD，∴∠BAC=∠ACD.∵∠B=∠D，AC=CA， △ABC≌△CDA，∴AB=CD，原證成立．

評注解法1、2、3都是根據判定方法1，分別從同旁內角、同位角、內錯角來分析．解法4運用三角形全等，得邊角對應相等，根據判定1、2、3均可完成．學生經歷多角度思考過程，數學建模、分析、獨立解決數學問題、思考內驅力等能力得到提升．

實例2 在矩形中求線段長度運用不同知識去開拓學生思維，題目如下．

題目如圖5，在矩形ABCD中，AB=3，BC=4，BE⊥AC，垂足為點E．試求BE的長．

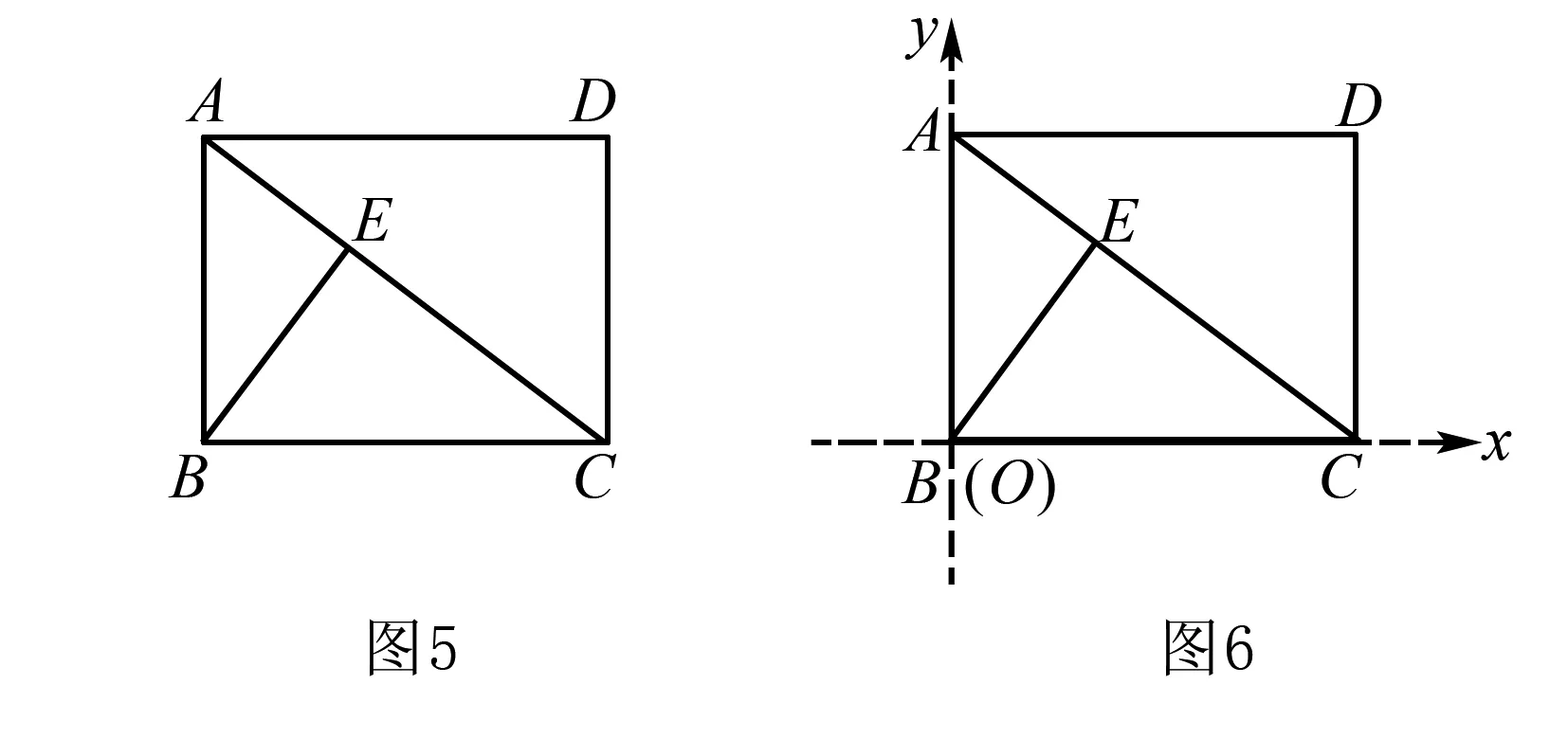
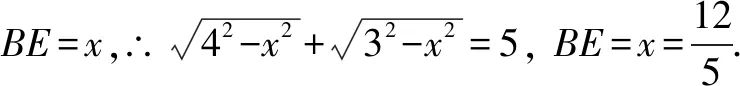
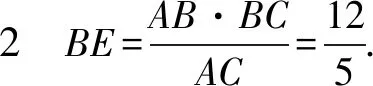
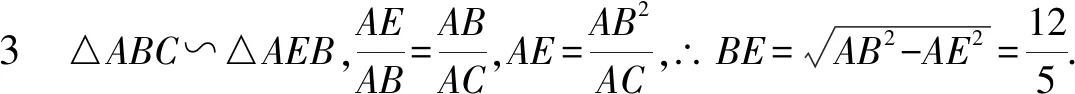
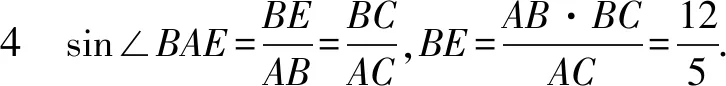
還可用代數法．在文獻[2]中，所謂代數法，就是將幾何命題中的有關線段、角度、面積等元素間的相互關系表示成相應的代數關系式，然后應用代數恒等變形或解方程等知識來給出幾何證明的一種方法．具體解法見思路5、思路6．

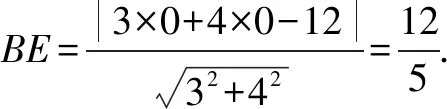
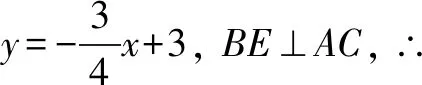
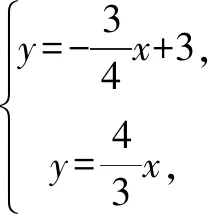
評注思路1建方程模型；思路2運用直角邊之積等于斜邊與其高之積；思路3運用三角形相似；思路4運用三角函數；解法5、6用代數方法．可以發現在這個過程中，學生數學綜合能力得到發展．

實例3在折疊問題中多角度分析畫圖，題目如下．

題目如圖7，在矩形ABCD中，點E在邊CD上，將該矩形沿AE折疊，恰好使點D落在邊BC上的點F處，請畫出點E，F的位置．

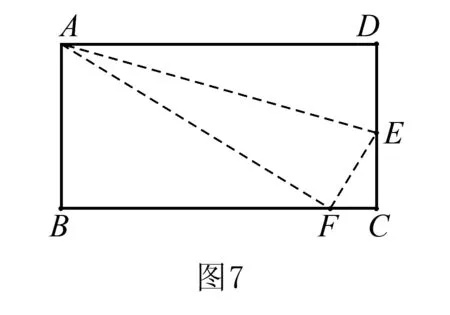
分析要畫出點E，F位置，可考慮先確定一個點，再確定另一個點．當△ADE≌△AFE時，AF=AD，以點A為圓心，AD為半徑畫弧交邊BC于點F，這樣點F的位置就確定了，下面確定點E位置．

思路1作∠FAD的平分線，交邊CD于點E．

思路2作∠AFE=∠D=90°，交邊CD于點E．

思路3作線段DF的垂直平分線，交邊CD于點E.

評注此題確定點E位置時，運用一題多解的方法，結合全等三角形、角平分線、線段垂直平分線、尺規作圖等數學知識，來進行數學推理及分析.在這個過程中，學生解讀文本、理解圖形結構等數學綜合能力得到提升．

通過以上實例，不難發現在數學教學過程中，如果能堅持運用一題多解來引導學生深入地去分析、研究問題，能夠有效提升學生數學綜合能力．