用動能定理研究滑動摩擦力作用下彈簧振子振動的終態位置和振動路程
張多生
(甘肅省武威第六中學 733000)
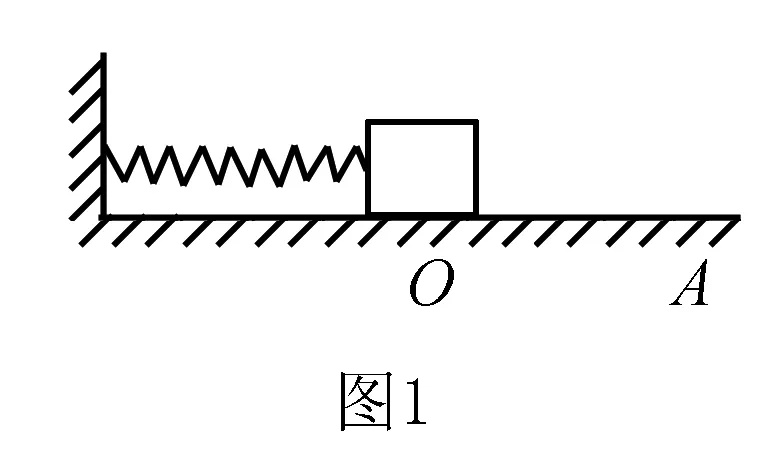
如圖1所示,勁度系數為k的一根輕質彈簧,左端固定在豎直墻壁上,右端連接一質量為m的小物塊,開始時彈簧處于原長,小物塊靜止于O點.將小物塊向右拉至A點,釋放后小物塊在粗糙水平面上左右振動起來.此裝置稱之為彈簧振子,小物塊稱為振子.由于摩擦,小物塊最終會停下來.已知小物塊與水平地面間的動摩擦因數為μ,最大靜摩擦力可看成滑動摩擦力的大小,為μmg.對于振子最終停留的位置,好多同學錯誤地認為一定停在O點.從動力學角度研究滑動摩擦力作用下彈簧振子的運動規律,高中學生限于數學知識,難于理解.本文從能量的角度探索滑動摩擦力作用下彈簧振子的運動規律,確定振子最終停留的位置及振動通過的路程.
一、平衡位置

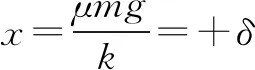
二、振子單向運動過程中相對于O點的最大位移的變化

彈力是變力,彈力做的功可以通過F-x圖象的“面積”求解.振子從O點運動到A點的過程中,彈簧的形變量等于小物塊的位移x,則彈力F隨位移x的關系為F=kx,F-x圖象如圖3所示.此過程中克服彈簧彈力F所做的功W為圖象與x軸圍成的面積,即


以彈簧自然伸長時振子的位置O為原點,建立直線坐標系,如圖4所示.把振子從右端最大位移x0處無初速釋放,振子開始左右振動.設x1、x2、x3、x4…依次為振動過程中振子離O點的最大位移.
振子沿ox軸負方向從x0處運動到x1(x1<0)處的過程中,由動能定理得出:

整理可得:
振子在x1處掉頭而回,沿x軸正方向運動,到達x2處的過程中,由動能定理繼續得出:
整理可得:
至此不難看出,只要我們交替運用(1)式和(2)式,就可以知道振子偏離O點的最大位移變化規律:
當振子向左運動時有:
x0+x1=x2+x3=x4+x5=…=2δ
當振子向右運動時有:
x1+x2=x3+x4=x5+x6=…=-2δ
即小物塊每經過一個單向運動后,對O點的最大位移大小按等差數列的規律遞減,遞減公差為2δ,即:
x0-|x1|=|x1|-x2=x2-|x3|=…=2δ(3)
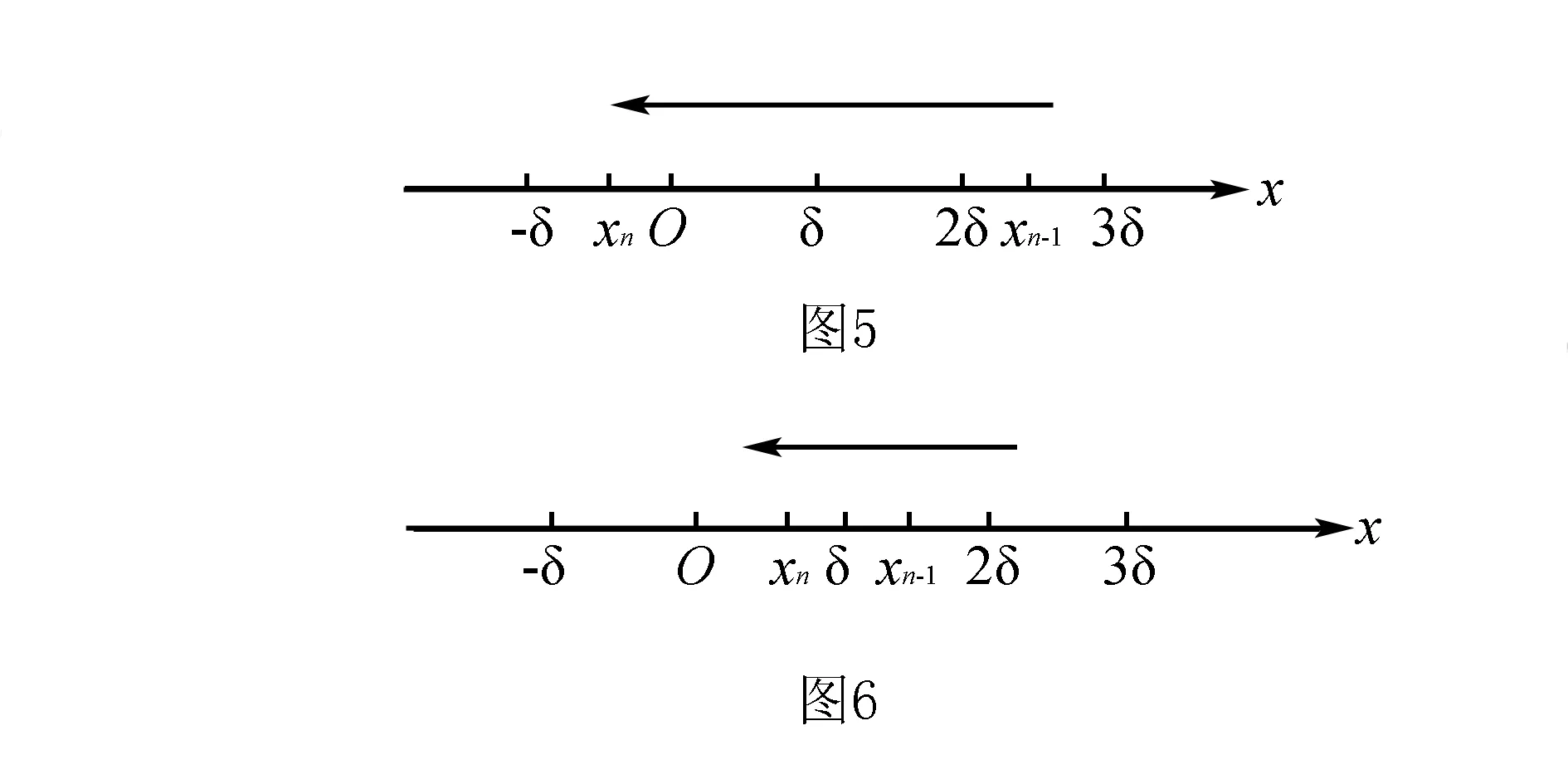
以上結論對最后一次單向運動可能不適用.最后一次單向運動有兩種可能性,如圖5和圖6所示.若最后一次單向運動途經0點,(3)式仍然成立;若最后一次單向運動只在O點一側運動,不經過O點,則最大位移大小之后為2δ.
三、振子最終停留位置
由(1)式和(2)式交替應用,可確定出振子運動過程中離O點的最大位移值,依次為
x0,x1=-(x0-2δ),x2=x0-4δ,x3=-(x0-6δ),…….
若振子經過n個單向運動后靜止,由以上規律可遞推出振子最終靜止的位置,為xn=(-1)n·(x0-2nδ)
到此,我們還沒有徹底確定振子的終態位置,還需要確定單向運動次數n.通過上面的分析研究可知
|xn|≤δ,δ<|xn-1|≤3δ
因x0-2nδ不一定大于零,由|xn|≤δ求解n比較麻煩.而x0-2(n-1)δ一定大于零,則
δ 在以上范圍內取符合條件的自然數n,即為振子單向運動的次數.n確定后,振子的終態位置也就確定了. 振子運動路程用逐段位移大小之和求得.參考最后一次單向運動情況(圖5和圖6),可得出以下結果: s=x0+2|x1|+2x2+…2|xn-1|+|xn| =x0+2(x0-2δ)+2(x0-4δ) +…2(x0-2(n-1)δ)+|x0-2nδ| 或s=x0+2|x1|+2x2+…2|xn-1|-|xn| =x0+2(x0-2δ)+2(x0-4δ) +…2(x0-2(n-1)δ)-|x0-2nδ| 在x0比δ不太大的情況下,套用上述規律計算終態位置和路程反而比較麻煩.采用遞推的辦法,思路比較清晰.根據振子對O點的最大位移大小遞減規律(公式(3)),依次寫出最大位移值,數出單向運動次數n,再計算振子運動的路程.比如,當x0=7.5δ時,最大位移依次為 7.5δ,-5.5δ,3.5δ,-1.5δ,-0.5δ 可知振子最終停留在x=-0.5δ處,單向運動次數為n=4.結合運動示意圖求出的路程為s=7.5δ+2×5.5δ+2×3.5δ+2×1.5δ-0.5δ=28δ 在x0比δ大的多的情況下,就得推理最大位移的變化規律,確定單向運動次數,再用數列知識求路程.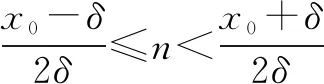
四、振子運動的路程
五、結論應用

