初高中數學銜接知識及思想方法探究之復合函數問題

劉浩州

(福建省泉州實驗中學 320006)

“銜接”意指將兩個分開的物體間的連接，這里指初中和高中數學的教學內容和數學思想方法上的連接.但并不意味著將高中的知識內容提前教學或者把高中的試題放在初中考查，而是從高中教學內容和數學思想的剛性需求出發，研究初中階段應該滲透的數學思想以及知識預備，然后在初中的教學中以及初中學業結束后在銜接內容上設置合適的題目或者知識點.事實上，初高中教學的銜接不僅僅關注顯性的知識，更應關注蘊涵在知識中的數學思想，關注引導學生逐步形成適應高中數學教學的學習習慣和思維方式.本文例舉的例題主要是復合函數部分內容，可以變式為銜接階段的試題也可以作為高中階段復合函數專題訓練的案例.

一、例題及解析

例1已知函數f(x),g(x)：

x0123f(x)2031

x0234g(x)2103

則函數y=f(g(x))的零點是( ).

A.0 B.1 C.2 D.3

答案：C

復合函數經常使用換元法對某個整體進行換元，方便計算也方便理解.本題考查的一個主要能力是對換元的使用，不管所求目標函數多復雜，要先看到對應關系是“f”，求函數f(x)的零點，借助第一個表格找到f(t)=0的解為t=1，然后通過第二個表格找到t=g(x)=1，顯然x=2.由于初中階段的函數表示形式還沒有學習映射概念，“零點”也沒有學習過，但是換元法接觸過，此題可以針對換元法為學生做好必要訓練和知識預備.

變式：已知y是關于t的函數，t是關于x的函數，并且有以下條件：

t0123y2031

x0234t2103

則使得方程y=0成立的x的值是( ).

A.0 B.1 C.2 D.3

例2若方程2sin2x+sinx-m=0在[0,2π)上有且只有兩解，則實數m的取值范圍是____.

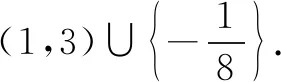
此題考查了對復合函數圖象的理解，綜合考查了高中數學思想方法中數形結合、化歸與轉化思想的應用.高中階段的解題可以利用二次函數與三角函數的圖象解決，也可以分離參數將方程的解轉換為函數圖象的交點.由于涉及的三角函數圖象是初中學生所沒接觸過的，因此可以這樣變式：

變式1關于x的方程2(-x2+2x)2-3(-x2+2x)+1=0的解的個數為____.

計算思維[1]的英文釋義是Computational thinking，顧名思義，即是將計算機的思維用在人的思考里。拓展開來，便是我們用計算機的基礎概念、計算方法、語言邏輯等去思考、設計和解決人的問題。

答案：3個

變式2若方程2(-x2+2x)2+(-x2+2x)-m=0在-1≤x≤3上有且只有兩解，則實數m的取值范圍是____.

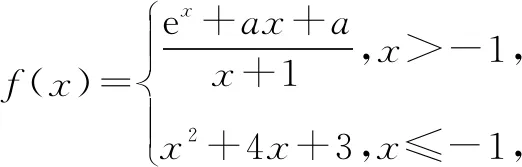
A.4個 B.7個 C.10個 D.12個

答案：D.

本題考查了分段函數的理解，充分考驗了學生分類與整合的能力，同時也對復合函數有較大的能力要求.在學生了解了函數運用y=f(x)的表達形式之后可以考慮變式為：

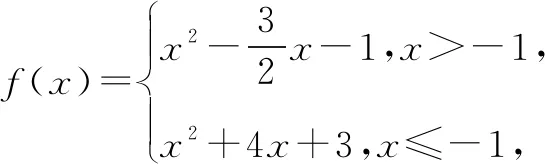
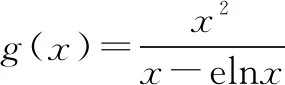
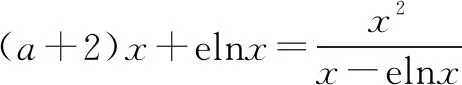
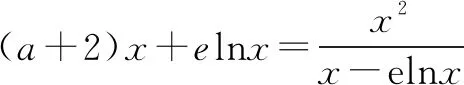
由二次方程根的分布及二次函數圖象特征，設φ(t)=t2+(a+1)t-a-1，則

解得a>-1.

例4考查了將函數圖象的“交點”問題轉換為方程的解或者函數的零點，這是高中函數部分很重要的方法，也是數形結合融會貫通的一個表現.由于此題涉及的函數相對復雜，方法上運用的求導，較難直接變式成初中的題目，但是可以在高中復合函數教學中作為典型例題.

函數的知識及涉及的思想是初高中都必須掌握的內容，也是體現數學核心素養中數學抽象與邏輯推理的重要表現形式．例1作為基礎的抽象函數，對培養學生數學抽象的素養有很大幫助，后面三道例題對培優學生邏輯推理的素養以及鍛煉學生分類討論、數形結合及轉化與化歸能力也有很大幫助.

二、總結

高中數學課程應注意提高學生的數學思維能力，這是數學教育的基本目標之一.教師作為學生建構主義學習的引導者，通過對知識和問題的形成過程的研究，設置幫助學生建構知識的題目，關注學生銜接過程中需要的知識，從而幫助學生運用所學知識和已有的經驗主動建構富有意義的理解.這也是培優數學核心素養的一個重要方面.