電容綜合問(wèn)題中的短暫過(guò)程與持續(xù)過(guò)程
陶漢斌
(浙江省金華第一中學(xué) 321015)
一、RC電路的一般特征
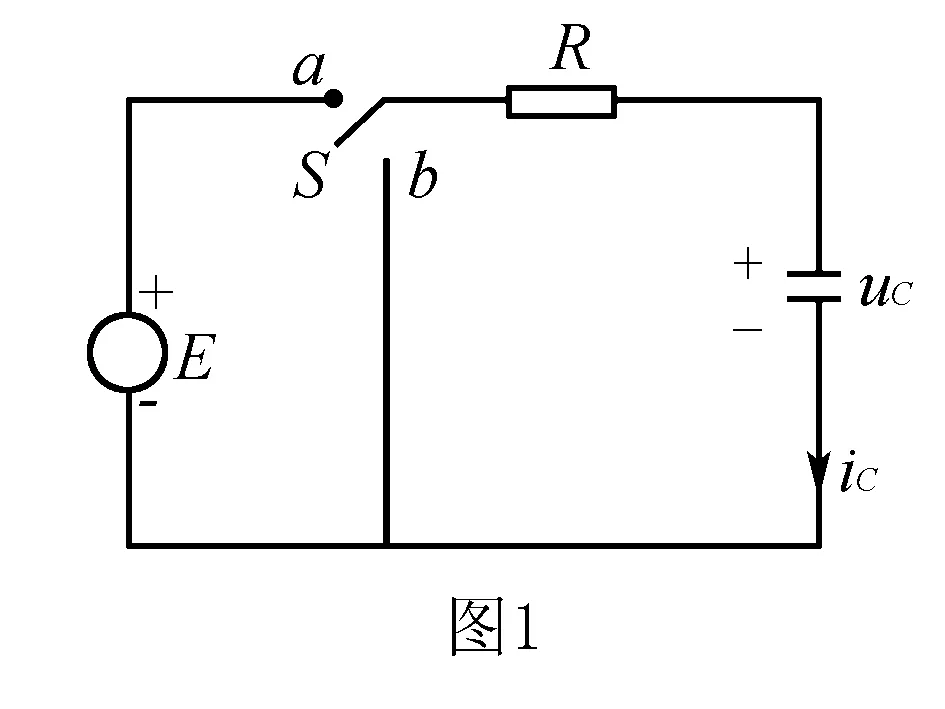

當(dāng)uc=E時(shí),i=0,充電過(guò)程結(jié)束.試驗(yàn)證明,充電過(guò)程可用下面公式進(jìn)行描述,即

從公式中不難看出,充電過(guò)程中uc和i是按指數(shù)規(guī)律變化的,而充電的快慢取決于電阻和電容的乘積,因此稱RC為時(shí)間常數(shù)τ,即τ=RC.如果R和C的單位取歐姆和法拉,則τ的單位為秒.從中可以看出,τ越大充電越慢.當(dāng)t=3τ時(shí),uc=0.95E,當(dāng)t=5τ時(shí),uc=0.993E.一般認(rèn)為當(dāng)t=3τ~5τ時(shí),電容器上的電荷已被充滿.我們可用圖2所示的圖線來(lái)直觀理解電容器充電過(guò)程中電流與時(shí)間的關(guān)系.

當(dāng)t=4τ~5τ時(shí),工程上即認(rèn)為電容的初始儲(chǔ)能已被全部消耗,也就是放電完畢.其放電過(guò)程的中電流與時(shí)間的關(guān)系與如圖2相仿.
當(dāng)然,如果當(dāng)開關(guān)打接到a充電時(shí)電容器的初始電壓uc不為零,那么充放電過(guò)程的公式將更加復(fù)雜,在這里就不進(jìn)行討論了.
二、理解短暫過(guò)程與持續(xù)過(guò)程
在RC電路中,充放電的快慢取決于電阻和電容的乘積,因此稱RC為時(shí)間常數(shù)τ.當(dāng)t=5τ時(shí)電容器充放電基本完成,那么這個(gè)5τ時(shí)間能否理解為“瞬間”的短暫過(guò)程呢?還是應(yīng)該理解為一個(gè)較長(zhǎng)的持續(xù)過(guò)程呢?
我們可以設(shè)想在12V電源上充電,理想狀態(tài)電池沒有內(nèi)阻,連接的導(dǎo)線也沒有電阻,τ=RC=0,充電時(shí)間等于0,瞬間電流無(wú)窮大,這當(dāng)然就應(yīng)該理解為“瞬間”的短暫充電過(guò)程.同理如果電容器放電的過(guò)程中電路中的所有電阻都可忽略不計(jì),比如用一根足夠強(qiáng)度的金屬絲,直接短路電容器兩端使它放電,則由于金屬絲長(zhǎng)度很短,電阻很小,造成短路電流很大,電容器儲(chǔ)存的電荷瞬間被釋放完畢,這也是“瞬間”的短暫放電過(guò)程.
在實(shí)際的電路中肯定存在一定的電阻,比如整個(gè)電路的等效電阻為1Ω,電容器的電容為1000uF,時(shí)間常數(shù)τ=RC=1ms,充放電的時(shí)間可認(rèn)為就是5τ=5ms,這個(gè)過(guò)程就可理解為較長(zhǎng)的持續(xù)過(guò)程.如果我們將電容器換成1F的超級(jí)電容,那么時(shí)間常數(shù)τ=RC=1s,充放電的時(shí)間就是5τ=5s,這應(yīng)該是一個(gè)相當(dāng)?shù)拈L(zhǎng)的持續(xù)過(guò)程了.這種短暫過(guò)程與持續(xù)過(guò)程,在經(jīng)典力學(xué)中涉及動(dòng)量守恒問(wèn)題時(shí)也常常有這兩種過(guò)程的分析.
三、典型錯(cuò)例欣賞


(1)導(dǎo)體棒獲得初速度v0時(shí),電容器的帶電量;
(2)導(dǎo)體棒上滑過(guò)程中加速度的大小
(3)求導(dǎo)體棒從最高點(diǎn)滑到低端的時(shí)間.
解析本題從力與能量?jī)蓚€(gè)角度分析電磁感應(yīng)現(xiàn)象,根據(jù)法拉第電磁感應(yīng)定律、歐姆定律和電流的定義式推導(dǎo)出電流與加速度的關(guān)系是解題的關(guān)鍵.對(duì)于第2小題導(dǎo)體棒切割類型,關(guān)鍵要正確受力分析,把握其運(yùn)動(dòng)情況和能量轉(zhuǎn)化關(guān)系.
(1)【霧里看花】
當(dāng)導(dǎo)體棒獲得初速度v0時(shí)將產(chǎn)生感應(yīng)電動(dòng)勢(shì),電容器的電壓等于此時(shí)導(dǎo)體棒切割磁感線產(chǎn)生感的應(yīng)電動(dòng)勢(shì),即
U=E=BLv0
此時(shí)電容器的帶電量為
q=CU=CBLv0
【正本清源】 由于電容與導(dǎo)體構(gòu)成的回路中,整個(gè)回路的電阻為0,電容器初始電壓為0,電容器充電的過(guò)程是一個(gè)短暫的過(guò)程.在這個(gè)短暫的過(guò)程中,導(dǎo)體棒的電流為無(wú)窮大,它將受到很大的安培力作用(此時(shí)重力可忽略),在瞬間安培力的作用下導(dǎo)體棒的速度發(fā)生突變而位置不變,這類似經(jīng)典力學(xué)中的瞬間碰撞過(guò)程.我們可在這個(gè)短暫的過(guò)程對(duì)棒應(yīng)用動(dòng)量定理
-BiL·Δt=mv-mv0
而充電的電流


mgsinθ-F安=ma
又F安=BiL,

聯(lián)立方程可解得

導(dǎo)體棒的運(yùn)動(dòng)是向上做勻減速運(yùn)動(dòng)的一個(gè)持續(xù)過(guò)程.
(3)【霧里看花】上滑過(guò)程中導(dǎo)體棒做勻減速運(yùn)動(dòng),由運(yùn)動(dòng)學(xué)公式求出導(dǎo)體棒上滑的最大距離.對(duì)于下滑過(guò)程運(yùn)用動(dòng)量定理和積分法求導(dǎo)體棒的運(yùn)動(dòng)時(shí)間.

以最大速度勻速下滑時(shí)
導(dǎo)體棒下滑的過(guò)程中,由動(dòng)量定理可得
mgsinθ·t1-I安=mv1-0



mgsinθ-F安=ma
所以開關(guān)打到a后做勻加速度直線運(yùn)動(dòng)

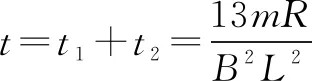


以最大速度勻速下滑時(shí)
解得最大速度為
導(dǎo)體棒下滑的過(guò)程中,由動(dòng)量定理可得
mgsinθ·t1-I安=mv1-0


開關(guān)打到a時(shí)為瞬間的短暫過(guò)程,這個(gè)過(guò)程速度v1會(huì)發(fā)生突變,我們對(duì)這個(gè)短暫的過(guò)程對(duì)棒應(yīng)用動(dòng)量定理-BiL·Δt=mv2-mv1


此過(guò)程中電容器的充電量為q′=CBLv2
然后導(dǎo)體棒做勻加速度運(yùn)動(dòng)對(duì)電容器繼續(xù)充電,根據(jù)牛頓第二定律mgsinθ-F安=ma
同樣我們可解得
所以開關(guān)打到a之后的持續(xù)過(guò)程中,導(dǎo)體棒做勻加速度直線運(yùn)動(dòng),由運(yùn)動(dòng)學(xué)公式




