評析 “氣缸”知識點

商文洪

(江蘇省蘇州市吳江區(qū)汾湖高級中學(xué) 215211)

一、平衡問題

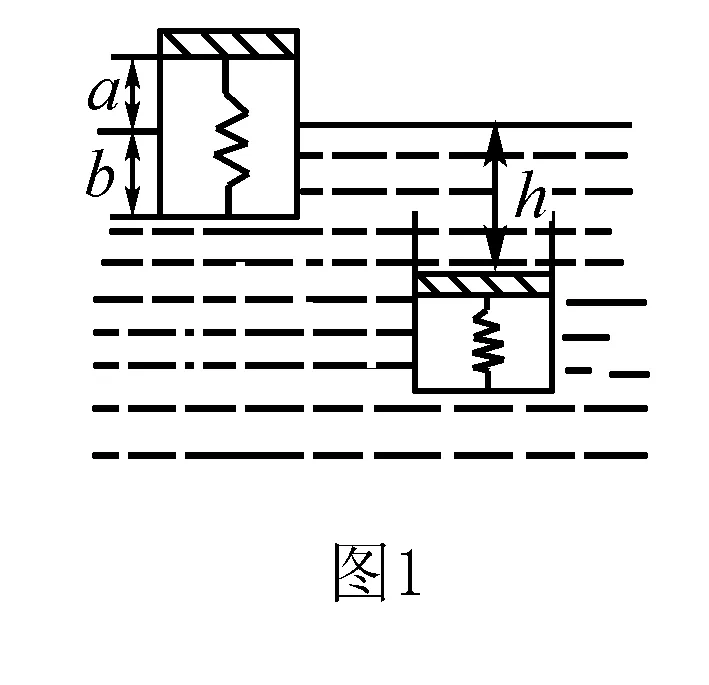
例1一圓形氣缸，上蓋一個重量不計的不漏氣活塞.在活塞和缸底裝有一根輕質(zhì)彈簧，封閉著壓強為p0的空氣，(如圖1所示)．氣缸浮在水面時，以水面到活塞距離a，缸底到水面距離b，活塞面積S，彈簧倔強系數(shù)為k，水的密度為ρ.設(shè)將氣缸緩慢地按入水中，當(dāng)活塞距水面深度為多大時,氣缸仍可能浮在水中．(氣缸在浸入水的過程中溫度不變,大氣壓強為p0)．

解當(dāng)氣缸浮在水面時，氣體壓強p1=p0.體積V=(a+b)S．且氣缸的重量等于浮力，即Mg=ρgbs.設(shè)按入水中深度距水面為h時仍能浮在水中，此時氣體體積V2=bS．由平衡條件得p0S+ρghS=p2S+ka,即p2=p0+ρgh-ka/s.根據(jù)玻馬定律plVl=p2V2有p0(a+b)s=(p0+ρgh-ka/s)bS,解得h=(p0as+kab)/ρgbs.

點評從例題求解不難可以發(fā)現(xiàn)，解題的關(guān)鍵是對氣缸進(jìn)行正確的受力分析，通過平衡條件找出壓強與其他物理量的關(guān)系，再用氣態(tài)方程解得．

二、動力學(xué)問題

例2放在光滑地面上的氣缸，缸體質(zhì)量為2千克,活塞質(zhì)量為1千克(如圖2所示)．靜止時活塞距缸底10cm，活塞面積為100cm2，外界大氣壓p0為1×105帕．現(xiàn)用水平推力F向左推活塞，活塞和氣缸以共同的加速度向左加速運動，這時活塞和氣缸底的距離變?yōu)?厘米，在不計活塞和氣缸摩擦、不漏氣及溫度不變的條件下，求水平推力F.

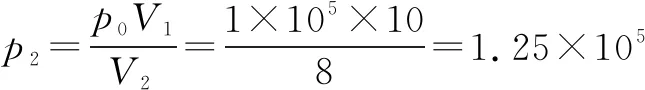
例3如圖3所示，氣缸質(zhì)量為8kg,活塞質(zhì)量是2kg,活塞橫截面積100cm2.當(dāng)繩索松馳時，缸底空氣柱長為0.5m，大氣壓強p0為1×105帕.活塞摩擦不計，g取10m/s2,現(xiàn)用160N的外力F通過滑輪拉氣缸離地，求最后氣缸內(nèi)空氣柱長度.

解當(dāng)繩子松馳時，缸內(nèi)氣體壓強p1=p0+mg/s體積V1=l1S.用力拉氣缸使其離地時，由于F>(M+m)g故氣缸整體向上加速，穩(wěn)定后作向上的勻加速直線運動.對整體和活塞分別用牛頓第二定律得

F-(M+m)g=(M+m)a及F+p2S-p0S-mg=ma

解得p2=p0-[MF/(M+m)s]

根據(jù)玻馬定律，p1V1=p2V2有(p0+mg/S)l1S=[p0-MF/(M+m)s]·l2S

解得L2=[(p0+mg/s)l1]/[p0-MF/(M+m)]

代入數(shù)據(jù)得l2=0.58m.

點評以上兩例題可知此類氣缸問題的解法是“整分結(jié)合”即先對氣缸整體分析，后隔離活塞分析.利用牛頓第二定律分別列方程求解，得氣體壓強p與力之間的關(guān)系，這樣問題就迎刃而解.

三、守恒問題

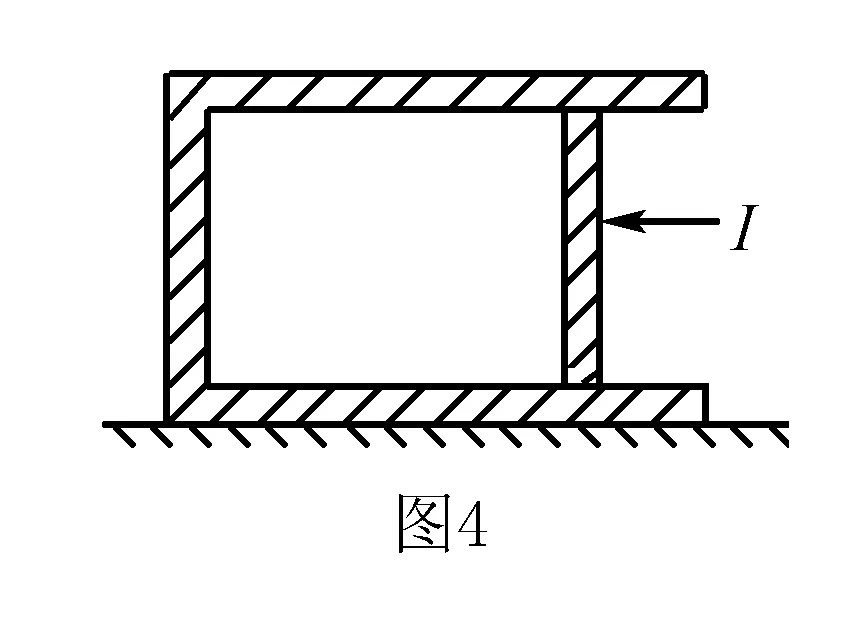
例4一水平放置在光滑面上的氣缸，用活塞封有部分理想氣體，氣缸和活塞的質(zhì)量都是m.如圖4，現(xiàn)給活塞施一個向左沖量，大小為I使其向左運動，則在以后的運動中被封閉氣體內(nèi)能改變的最大值是多少.

解先根據(jù)動量定理，在給活塞沖量I，活塞產(chǎn)生的速度v=I/m,然后活塞向左運動，由于氣體作用，活塞做減速運動，氣缸作加速運動.當(dāng)兩者速度達(dá)到某一值時，氣體壓縮最大，內(nèi)能改變也最大，活塞和氣缸速度變化過程中，系統(tǒng)的動量和能量守恒.

把v=I/m代入解得ΔE=3I2/8m.

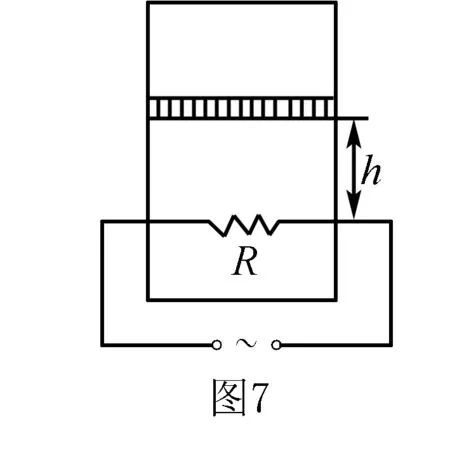
例5如圖5所示，一封閉氣缸上部為真空下部是一定質(zhì)量的理想氣體.中間活塞重為G，可在氣缸內(nèi)做無摩擦的滑動，距底高為h，氣缸底部有一根電阻為R的電阻絲，現(xiàn)加上交流電u=Umsinωt,經(jīng)時間t后活塞高度變?yōu)閔′.試求：(1)氣缸的內(nèi)能改變多少？(2)氣體的末溫度T(設(shè)氣體初溫為T).

解(1)當(dāng)電阻絲加熱t(yī)秒放出的熱量

又因為氣缸上部為真空，所以F=G，故氣體體積增大時是恒力做功，即W=Fs=G(h′-h).

點評運用能量守恒的觀點是解決熱力學(xué)現(xiàn)象的基本方法之一.遇到上述氣缸問題，需注意模型的識別，找出新舊模型之間的聯(lián)系和本質(zhì)區(qū)別，有些氣缸問題表面看好象是氣體性質(zhì)問題，其實質(zhì)應(yīng)用能量守恒規(guī)律解決.

四、多缸問題

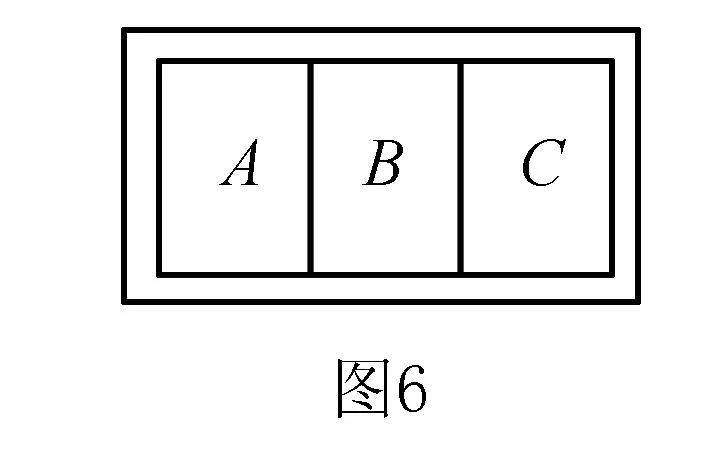
例6如圖6所示，密封絕熱容器中盛有27℃ 1個大氣壓的理想氣體，現(xiàn)將容器中間用兩個絕熱而能自由滑動的活塞將容器分成A、B、C三個相等部分，每部分的體積均為V0．當(dāng)A部分加熱到227℃，B部分加熱到327℃，C部分不變，則C部分體積是多少?

解加熱重新平衡后，三部分壓強仍然相等pA=pB=pC由理想氣體狀態(tài)方程可得

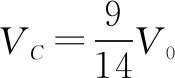
例7水平放置的固定氣缸A、B內(nèi)用活塞密封的空氣壓強都是p0，溫度T0，體積分別為V1和V2.兩個活塞的面積分別為S1和S2，用連桿連在一起，連桿所在空間真空.現(xiàn)將A筒空氣加熱到T1，B筒保持不變，求平衡時A筒內(nèi)氣壓多大?

解對A容器，由理想氣體狀態(tài)方程得p0V1/T0=pAV1′/T1

對B容器，由玻-馬定律得p0V2=pBV2′重新平衡后，對連桿和兩活分析有

pAS1=pBS2

又變化前后氣缸內(nèi)氣體的總體積不變，即V1+V2=V1′+V2′

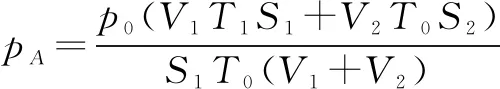
多缸問題可以用“一分為二”、“合二為一”的方法去解.“一分為二”就是分別研究氣缸內(nèi)各部分氣體狀態(tài)參量的變化，找出它們各自遵守的規(guī)律；“合二為一”就是通過研究各部分氣體間的關(guān)系，找出它們之間的物理和幾何條件.如各部分壓強相同，變化有前后總質(zhì)量不變，容器總體積不變等等.最后聯(lián)合求得.