勾股化在高中數學的滲透

楊偉達

(廣東省廣州市花都區第二中學 510800)

在高中數學學習中，一個熟悉而不容忽視的處理方法——“勾股化”.它參透到高中數學許多章節,統領各章節的核心．其實有關“勾股化”問題本是古老而陳舊的數學話題．它不外乎從數的角度或者從形的角度去賞析，吸引著許多數學教育工作者的關注.為此，那些命題專家們總是想方設法，常常把“勾股化”推廣到解決許多數學問題的關鍵，力求體現出濃濃的數學味．

一提取

例1(2013年全國卷Ⅰ)設當x=θ時，函數f(x)=sinx-2cosx取得最大值，則cosθ=____.

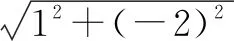
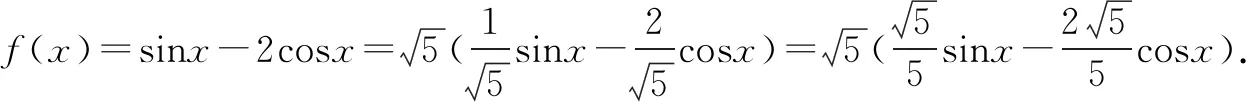
有這樣的一類三角函數題——“已知值求角”.僅從數的角度看，就是列方程組求解；若從形的角度看，構造一個直角三角形，利用三角函數的定義求解，方顯巧和快.前者是常見的通性通法，適合解答題，是考試的得分點；后者是特性特法，適合選擇題、填空題.因此，觀察、分析數組的特性，構建一個直角三角形，勾股化處理，起到快速、便捷的效果.

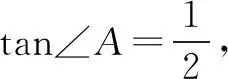
三、 “勾股數組”配湊

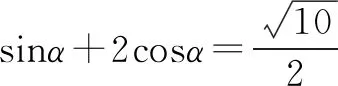
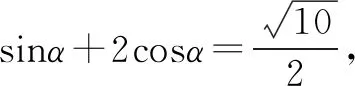
sin2α+cos2α=1. ②

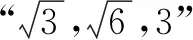
解因為α為第二象限,所以sinα>0，cosα<0.

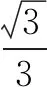
不妨構造直角三角形,

解得m=15.

四 、“a2+b2=c2”求解

對于這樣的一類立體幾何試題，已知條件中標明邊的長度.而長度的作用：一方面通過轉化和化歸求其它邊或角；另一方面利用勾股化證明垂直.因此，在解題過程中列方程組求解也是解題策略中的常見手法.

分析三棱錐內接球問題若直接找球心，不少學生難于找到球心的準確位置，以至于此問題無法求解；若能聯想到長方體外接球問題，可根據三棱錐主要性質特征構造長方體，則球心就是長方體對角線的中點，此時解決有關球問題就可轉化為長方體對角線來求解.

解由于已知三棱錐外接球問題主要性質特征滿足長方體的某部分特征,如圖2所示，構建長方體.

設AM=a，MD=b，MC=c.

設球心O到平面ABC的距離為h.

故選B.

總之，通過上面的例子，進行勾股化處理.這樣有利于培養學生的思維品質，從而不斷提高學生的思維能力，進而有利于培養學生思維的創造性.