一“網”打“盡” 精準教學
——以y=Asin(ωx+φ)的圖象性質為例

李昌成 曾 靜 車燕昭

(新疆烏魯木齊市第八中學 830002)

三角函數的公式多，性質多，題型多，學生容易混淆出錯.針對這種現狀，本人在高三復課時采取了“集中殲滅”的策略開展教學，也就是老師先把公式、性質講清楚，督促學生把公式、性質記牢固并理解，然后集中應用，對比學習，區別對待，達到掌握的目的.現舉一例，以饗讀者.

題目已知f(x)=2(cos2x+sinxcosx)，

(1)求f(x)的最小正周期；

(3)求f(x)的單調遞增區間；

(4)求f(x)圖象的對稱軸方程；

(5)求f(x)圖象的對稱中心；

(6)解不等式f(x)>1；

(7)y=sinx的圖象經過怎樣的變換，能變成f(x)的圖象？

(8)f(x)是偶函數嗎？若不是，怎樣變換可以使其成為偶函數？

(9)在△ABC中，f(A)=2，BC=2，求△ABC的面積的最大值.

注:這里練習了二倍角公式、擴角降冪公式、輔助角公式等重要的三角公式.公式只有用在應用中才能記牢用活，才能進一步地理解它們的內在聯系.

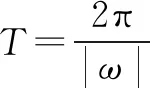
注:本問凸顯了函數中定義域優先的要求，也反映了三角函數整體非單調的特性，這是很多學生容易忽視的.

注:本問鞏固了y=Asin(ωx+φ)的單增區間的求法，還可以進一步回顧該函數單減區間怎么求？限定定義域的單調區間怎么求？y=Acos(ωx+φ)、y=Atan(ωx+φ)的單調區間怎么求？還有若A<0，該注意什么？這些問題不復雜，但是重要，必須全面總結，不可疏漏，分類掌握.

注:解三角不等式可以利用三角函數圖象取解集，一般要求在一個周期內的圖象連續即可.也可利用三角函數線取解集.

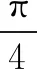
注:三角函數圖象變換通常有兩種方式：

①先做相位變換，再做周期變換，再做振幅變換，最后上下平移，即：y=sinx→y=sin(x+φ)→y=sin(ωx+φ)→y=Asin(ωx+φ)→y=Asin(ωx+φ)+k;

注:這類因平移導致奇偶性變換的問題要緊緊依靠誘導公式實現目的.解題依據是：f(x)=Asinωx、f(x)=Atanωx是奇函數，f(x)=Acosωx是偶函數.

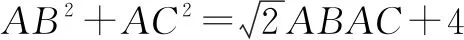
由均值不等式得AB2+AC2≥2AB·AC②.

注：三角函數圖象性質與解斜三角形有機結合實現了學以致用的教學目的，在高考中此類題型以解答題出現，注意準確使用正弦定理、余弦定理、面積公式、誘導公式、均值不等式等知識.

通過這一題，我們鞏固加深了對三角公式、三角函數的定義域、值域、單調性、奇偶性、對稱軸、對稱中心等性質、圖象變換規則以及解斜三角形的理解.各問題間既有區別，也有聯系，在比較中促進知識升華，將零散的知識串成了一條線，學生的收獲多多.這種一網打盡的教學案例很多，同仁可以嘗試這種教學，避開題海戰術.