基于應(yīng)用背景的旋轉(zhuǎn)體體積的教學(xué)設(shè)計(jì)
張瑩 許勇 武海波

摘要:本文采用啟發(fā)式和問題驅(qū)動(dòng)式教學(xué)方法,從旋轉(zhuǎn)體的構(gòu)成方式入手,借助硬幣旋轉(zhuǎn)的實(shí)例探究,引出了旋轉(zhuǎn)體的概念;隨后繼續(xù)利用“硬幣”的形象化分析,建立了旋轉(zhuǎn)體體積的求解方法,并將其應(yīng)用到實(shí)際問題中。
關(guān)鍵詞:高等數(shù)學(xué);教學(xué)設(shè)計(jì);旋轉(zhuǎn)體體積
中圖分類號(hào):O13 ? ? 文獻(xiàn)標(biāo)志碼:A ? ? 文章編號(hào):1674-9324(2019)20-0050-02
《高等數(shù)學(xué)》是高等院校理工類各專業(yè)的公共基礎(chǔ)課,其因較強(qiáng)的邏輯性、抽象性、應(yīng)用性,有利于訓(xùn)練學(xué)生的抽象思維、邏輯思維和解決實(shí)際問題的能力,是開展素質(zhì)教育、培養(yǎng)學(xué)生創(chuàng)新精神和創(chuàng)新能力的重要課程[1]。定積分應(yīng)用中的微元法精妙地體現(xiàn)了“化整為零、積零為整”的思想,它對(duì)于微積分的學(xué)習(xí)和理解具有重要的理論價(jià)值和實(shí)際意義。但是學(xué)生在學(xué)習(xí)用微元法解決旋轉(zhuǎn)體體積計(jì)算問題時(shí),通常對(duì)旋轉(zhuǎn)體的空間構(gòu)成理解不夠深入,在微元的選擇上容易與后續(xù)學(xué)習(xí)的柱殼法相混淆。因此,本設(shè)計(jì)采用啟發(fā)式和問題驅(qū)動(dòng)式教學(xué)方法[2-3],在形象化展示抽象數(shù)學(xué)概念的基礎(chǔ)上,提出問題、引起興趣、引發(fā)思考,最終實(shí)現(xiàn)知識(shí)的正確掌握與方法的深入理解,并將其應(yīng)用到實(shí)際中去。
一、教學(xué)設(shè)計(jì)思路
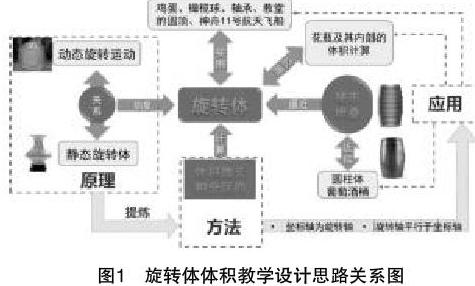
本設(shè)計(jì)從芭蕾舞演員和旋轉(zhuǎn)木馬的動(dòng)態(tài)旋轉(zhuǎn),以及花瓶、雞蛋、橄欖球和航天器的旋轉(zhuǎn)結(jié)構(gòu)入手,提出動(dòng)態(tài)旋轉(zhuǎn)和靜態(tài)旋轉(zhuǎn)結(jié)構(gòu)之間的關(guān)系問題[4]。進(jìn)而,通過分析硬幣旋轉(zhuǎn)構(gòu)成球體的小游戲,將“動(dòng)”與“靜”相結(jié)合,引入旋轉(zhuǎn)體的概念。隨后,繼續(xù)利用硬幣堆疊來逼近圓柱體體積,并將其推廣到更一般的旋轉(zhuǎn)體體積逼近與求解問題中,引出微元法的思想,進(jìn)一步運(yùn)用定積分建立求解旋轉(zhuǎn)體體積的積分公式,并用其求解典型旋轉(zhuǎn)體的體積。最后,利用該求解方法,計(jì)算花瓶及其內(nèi)部體積。教學(xué)設(shè)計(jì)思路關(guān)系如圖1所示。
二、教學(xué)過程
1.概念的引入。首先,提出花瓶及其內(nèi)部體積如何計(jì)算的問題;隨后,展示冰上芭蕾和旋轉(zhuǎn)木馬的運(yùn)動(dòng)視頻,以及自然界和人類社會(huì)中存在的多種靜態(tài)旋轉(zhuǎn)結(jié)構(gòu),如雞蛋、燈籠、陶藝作品、教堂的圓頂。通過“動(dòng)”與“靜”的對(duì)比,引出本節(jié)的研究對(duì)象及學(xué)習(xí)內(nèi)容。進(jìn)一步引導(dǎo)學(xué)生觀察旋轉(zhuǎn)硬幣的過程,探討“動(dòng)”與“靜”的關(guān)系,發(fā)現(xiàn)二維圖形旋轉(zhuǎn)構(gòu)成三維立體的邏輯關(guān)系,繼而給出旋轉(zhuǎn)體的定義,即由一個(gè)平面圖形繞所在平面內(nèi)一條定直線旋轉(zhuǎn)一周而成的立體,這條直線稱為旋轉(zhuǎn)軸。
2.旋轉(zhuǎn)體體積的計(jì)算。明確了旋轉(zhuǎn)體的定義后,又該如何根據(jù)其構(gòu)成特點(diǎn),尋找求解旋轉(zhuǎn)體體積的方法呢?圓柱作為最基本的旋轉(zhuǎn)體,可以借助半徑相同硬幣的堆疊來進(jìn)行逼近,即計(jì)算每個(gè)硬幣的體積,再相加即可獲得圓柱體的體積。對(duì)于更一般的情形,如葡萄酒桶的體積問題,引導(dǎo)學(xué)生分析圓柱體與葡萄酒桶體積問題的異同,提出問題啟發(fā)思考,即是否也可通過硬幣的累加來逼近葡萄酒桶的體積呢?不難發(fā)現(xiàn)這正是微元法的核心思想,通過細(xì)分、近似得到微元,就可以進(jìn)一步利用定積分來求得葡萄酒桶的體積,如圖2所示。這一個(gè)個(gè)堆疊的硬幣就是體現(xiàn)了體積微元的選擇,可見體積微元的選擇與計(jì)算都與旋轉(zhuǎn)軸的方向與位置有著密切的聯(lián)系。因此,關(guān)于旋轉(zhuǎn)體體積的計(jì)算可以根據(jù)旋轉(zhuǎn)軸和微元的關(guān)系分為兩大類來討論。
在掌握了兩類情形下旋轉(zhuǎn)體體積的計(jì)算方法后,課程中將通過例題展示不同情形的問題,在與學(xué)生互動(dòng)交流中,檢驗(yàn)學(xué)生對(duì)概念的理解和對(duì)方法的掌握程度。如:例1,計(jì)算由拋物線弧x=y2,y∈[0,1]與x軸、直線x=1圍成的圖形分別繞y軸和x軸旋轉(zhuǎn)一周所成旋轉(zhuǎn)體的體積;例2,求由曲線y=4-x2及y=0所圍成的圖形繞直線x=3旋轉(zhuǎn)所構(gòu)成的旋轉(zhuǎn)體的體積。
3.實(shí)際應(yīng)用。至此,我們已經(jīng)掌握了旋轉(zhuǎn)體體積求解的基本思路和方法。課程開始時(shí)提到的雞蛋和橄欖球等實(shí)際問題的體積如何求解呢?不妨以花瓶為例,想要求得花瓶及其內(nèi)部的整體體積,可分為五步:(1)建立恰當(dāng)?shù)闹苯亲鴺?biāo)系;(2)擬合平面曲線;(3)確定旋轉(zhuǎn)軸及積分變量和區(qū)間;(4)確定半徑函數(shù)并寫出積分式;(5)求解定積分得到體積。這樣,就可以通過建模的思想,借助本節(jié)課所學(xué)概念和方法實(shí)現(xiàn)實(shí)際問題的求解。
本節(jié)內(nèi)容是訓(xùn)練使用微元法的重要載體,對(duì)培養(yǎng)學(xué)生的數(shù)學(xué)建模能力、邏輯思維能力和抽象思維能力非常重要。通過硬幣的引入,使學(xué)生對(duì)問題的求解形成深刻且直觀的印象。在學(xué)習(xí)過程中,雖然會(huì)根據(jù)旋轉(zhuǎn)軸不同,分為多種情景進(jìn)行研究,但問題的核心不變,即把握微元法思想,明確微元選取方向與旋轉(zhuǎn)軸的關(guān)系,通過確定積分微元和積分區(qū)間,即可求得旋轉(zhuǎn)體的體積。在分析抽象數(shù)學(xué)問題的基礎(chǔ)上,進(jìn)一步分析花瓶及其內(nèi)部體積求解的實(shí)際問題,培養(yǎng)了學(xué)生利用微積分知識(shí)分析實(shí)際問題的能力。
參考文獻(xiàn):
[1]西北工業(yè)大學(xué)高等數(shù)學(xué)教材編寫組.高等數(shù)學(xué):下冊(cè)[M].第3版.北京:科學(xué)出版社,2013:50-57.
[2]鄭淑芬.案例教學(xué)法的作用、實(shí)施環(huán)節(jié)及需要注意的問題[J].教育探索,2008,3(4):56-57.
[3]陶沼靈.啟發(fā)式教學(xué)方法研究綜述[J].中國(guó)成人教育,2007,(7):139-140.
[4]郜舒竹,徐春華.對(duì)旋轉(zhuǎn)體體積的再認(rèn)知[J].數(shù)學(xué)通報(bào),2005,44(1):54-57.
- 教育教學(xué)論壇的其它文章
- 試論古文字輔助對(duì)外漢字教學(xué)的可行性
- 基于“互聯(lián)網(wǎng)+”的焊接技術(shù)與工程專業(yè)實(shí)驗(yàn)課程體系的構(gòu)建
- 基于應(yīng)用型人才培養(yǎng)的金屬材料及熱處理課程實(shí)驗(yàn)教學(xué)探究
- 物理化學(xué)實(shí)驗(yàn)3D虛擬教學(xué)系統(tǒng)開發(fā)
- 地方高校多學(xué)科融合的綜合實(shí)驗(yàn)教學(xué)體系的構(gòu)建及應(yīng)用
- 水生動(dòng)物免疫學(xué)實(shí)驗(yàn)的教學(xué)與實(shí)踐

