培養質疑習慣，從不盲信中考題開始

葉新和

摘要 不是所有的中考試題都是優秀試題。一線教師不應盲信中考試題，而應用審視的眼光來看待各地中考試題，進而逐漸形成質疑的意識與習慣。

關鍵詞 初中數學 中考題 質疑

教師具有良好的質疑習慣，是培養學生質疑習慣的基礎和前提。培養教師的質疑習慣可以從不盲信中考題開始。

中考題都是優秀試題嗎？我們不妨來看看某地的一道中考試題：

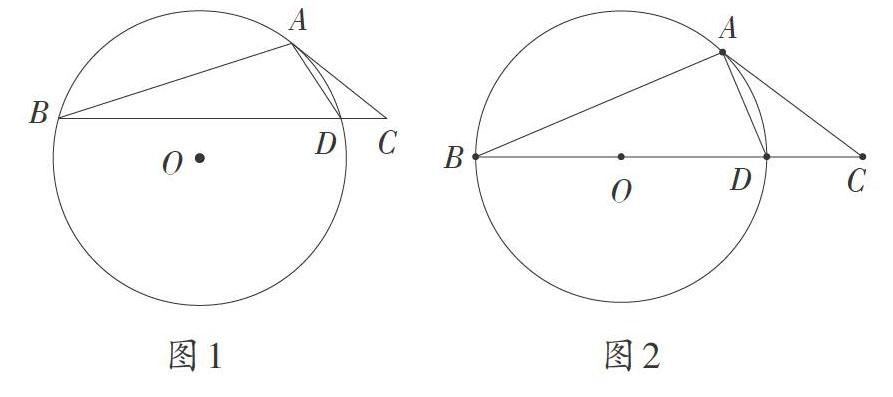
如圖1，在△ABC中，點D在邊BC上，∠ABC∶∠ACB∶∠ADB=1∶2∶3，⊙O是△ABD的外接圓。

（1）求證：AC是⊙O的切線;

（2）當BD是⊙O的直徑時（如圖2），求∠CAD的度數。

某雜志上一篇文章的解答思路為：

（1）若AC是⊙O的切線，則其應與過切點的直徑垂直。過AC與⊙O的交點作一條“直徑”，證明該直徑與AC垂直即可。

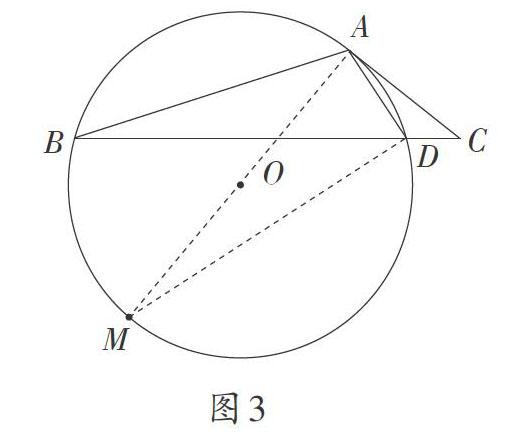
由此，如圖3，連接AO并延長，交⊙O于點M，則AM為⊙O的直徑，連接DM。由已知條件得出∠ABC =∠CAD。由直徑所對的圓周角為直角得出∠ADM =90°，證出∠AMD=∠ABC=∠CAD，得出MA⊥AC，即可得出結論。

（2）因為BD是直徑，可知其所對的圓周角∠BAD=90°，再根據∠ABC∶∠ACB∶∠ADB=1∶2∶3，得出∠ABC=22.5°，利用（1）的結果得出∠ABC=∠CAD，從而得出本小題的結論。

仔細分析該思路，發現存在兩個問題：

一是該思路中有一個“回路”。即第二小題在求∠ABC的度數后，∠ADB與∠ACB的度數也出來了，直接利用內外角的關系即可求出∠CAD的度數（∠CAD=∠ADB-∠ACB = 22.5°），該解答跟第一小題毫無關系。

二是第一小題的解答并不容易。因為由條件“∠ABC∶∠ACB∶∠ADB=1∶2∶3”，能夠得到的數量關系比較多，可以有：①∠ACB=2∠ABC;②∠ADB=3∠ABC;③∠ACB∶∠ADB=2∶3;④∠ADB=∠ABC+∠ACB等。能夠建立的數量關系越多，解答者越容易無所適從。

將第二小題解答中的“回路”去掉后，第一小題不容易解答顯得更為突出。

一、學生試答實驗

第一小題解答不容易的判斷是否正確？下面的實驗比較有說服力。……