全國名校導數(shù)測試卷答案與提示

一、選擇題

1.D 2.A 3.B 4.A 5.A 6.C 7.A 8.B 9.D 10.B 11.B 12.D 13.C 14.A 15.C 16.B 17.C 18.B 19.B 20.A 21.B 22.C 23.A 24.A 25.A 26.D 27.A 28.D 29.C 30.C 31.A 32.D 33.D 34.A 35.D 36.D 37.D 38.B 39.C

二、填空題

40.（- ∞，2） 41.142.2

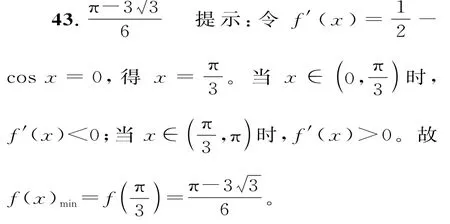
44.2x-y-3=0 提示:當x＞0時，-x ＜ 0，f(x)=-f(-x)=-[-xln

x-x+2]=xlnx+x-2，則f'(x)=ln

x+2，f'(1)=2。又f(1)=-1，則所求切線方程為y+1=2(x-1)，即2xy-3=0。

45.(-2，9) 提示:因為f(x)=2x2+1，所以f'(x)=4x。令4x0=-8，則x0=-2，f(x0)=9，點M 的坐標為(-2，9)。

47.(-1，+∞) 提示:由f(x)＞2x+4，得f(x)-2x＞4。令g(x)=f(x)-2x，則g'(x)=f'(x)-2＞0，g(x)在R上為增函數(shù)。又g(-1)=f(-1)+2=4，即g(x)＞g(-1)，故x＞-1。

50.[-4，0)∪(1，28] 提示:由f'(x)=6x2-6x=6x(x-1)，得f(x)在(0，1)上遞減，在[-2，0)和(1，2]上遞增，所以-28+a≤0＜-1+a或a＜0≤4+a，即a∈[-4，0)∪(1，28]。

52.（-∞，-3） 提示:令y'=aex+3=0，則ex=-。因此，-＞ 0。又-＜1，故a∈(-∞，-3)。

55.-2 提示:f'(x)=x2-x+a。又函數(shù)f(x)恰在 ［- 1，2］上單調(diào)遞減，故-1，2是f'(x)=0的兩根，a=(-1)×2=-2。

f(mx-2)＜-f(x)=f(-x)，x＜2-mx，即mx+x-2＜0，m∈［ - 2，2］。

58.1-ln2 提示:直線y=kx+b與曲線y=lnx+2，y=ln(x+1)均相切，設切點分別為A(x1，y1)，B(x2，y2)。由y=lnx+2得y'=，由y=ln (x+1)得則-1。故y1=-lnk+2，y2=-lnk，即。因為A，B 在 直 線y=kx+b 上，所 以

三、解答題

59.(1)f'(x)=3x2-x+b。

令f'(x)=0有兩個不相等的實根。

(2)因為f(x)在x=1處取得極值，所以f'(1)=0。

故3-1+b=0，得b=-2。

f'(x)=3x2-x-2=(3x+2)(x-1)。

12

故［f ( x)］max=2+c＜c2，解得c＞2或c＜-1。

故c∈（ -∞，-1）∪（ 2 ， +∞）。

因為f'(x)=x2，所以在點處的切線的斜率k=f'(1)=1。

則切線的斜率k1=f'(x0)=，即y=

整理得(x0+1)(x0-2)2=0，解得x0=-1或x0=2，故所求切線方程為x-y+2=0或4x-y-4=0。

因為x=4是函數(shù)f(x)=alnx+x2-12x+11的一個極值點，所以2×4-12=0，解得a=16。

經(jīng)檢驗a=16滿足題意，故a=16。

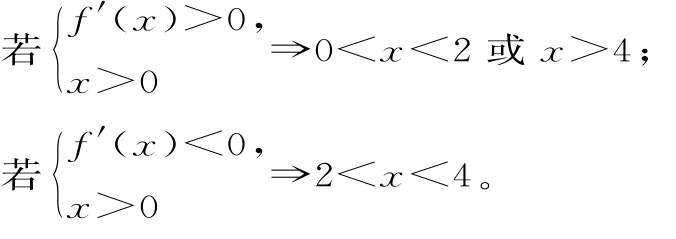
故f(x)的單調(diào)遞增區(qū)間是（0，2）和（4，+∞），單調(diào)遞減區(qū)間是（2，4）。

62.(1)f'(x)=-3x2+2ax+b。令解得a=3，b=9。

(2)由(1)知f'(x)=-3x2+6x+9。

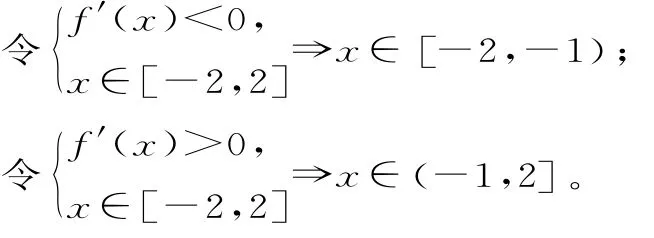
故此時函數(shù)f(x)的單調(diào)遞減區(qū)間為［-2，-1），單調(diào)遞增區(qū)間為（-1，2］。

解得f(-2)=8+12-18+c=2+c，f(2)=-8+12+18+c=22+c。

顯然，f(x)max=f(2)=22+c=20，得c=-2。

x=-1為f(x)在［ - 2 ，2］上的極小值點。

故f(x)min=f(-1)=-7。

63.(1)f'(x)=-xex(x∈R)。

令f'(x)=0，得x=0。

當x∈(-∞，0)時，f'(x)＞0，f(x)單調(diào)遞增;

當x∈(0，+∞)時，f'(x)＜0，f(x)單調(diào)遞減。

故f(x)max=f(0)=0。

(2)由(1)知，當x＞0時，f(x)＜0，g(x)＜0＜1。

當-1＜x＜0時，g(x)＜1等價于f(x)＞x。

設h(x)=f(x)-x，則h'(x)=-xex-1。

從而當x∈(-1，0)時，h'(x)＜0，h(x)在(-1，0)上單調(diào)遞減，h(x)＞h(0)=0，即g(x)＜1。

綜上，g(x)＜1。

64.(1)f'(x)=3x2+2mx+n，由題意知x=0是函數(shù)的一個極值點，于是f'(0)=0，得n=0。

(2)由(1)知f(x)=x3+mx2+p。

由題意知f(2)=0，即23+m·22+p=0，得p=-4(m+2)。

又f'(x)=3x2+2mx=0，得x=0或x=-。

由于f(x)在 ［0 ， 2］上是減函數(shù)，因此分析可得-≥2，得m≤-3。

故f(1)=1+m+p=1+m-4(m+2)=-3m-7≥2。

又因為f(2)=ln2-2，所以函數(shù)y=f(x)的圖像在點(2，f(2))處的切線方程為y-(ln2-2)=(x-2)，即x-2y+2ln2-6=0。

66.(1)f'(x)=3x2+2f'（）x-1。

令f'(x)=3x2-2x-1＞0，得x＜-或x＞1。故f(x)的單調(diào)增區(qū)間為（- ∞，-）和（ 1 ， +∞）。同理可得f(x)的單調(diào)減區(qū)間為（ -，1）。

(2)設sin x=t∈ ［- 1，1］，由(1)知f(x)在區(qū)間內(nèi)單調(diào)遞增，在區(qū)間內(nèi)單調(diào)遞減，故f(sinx)max=又f(-1)=f(1)=-1，故f(sinx)min=-1。

(2)由f(x)＜x+m，得f(x)-x＜m。

令g(x)=f(x)-x，即g(x)=(e-1)·x-lnx。

當x變化時，g'(x)，g(x)變化如表1:

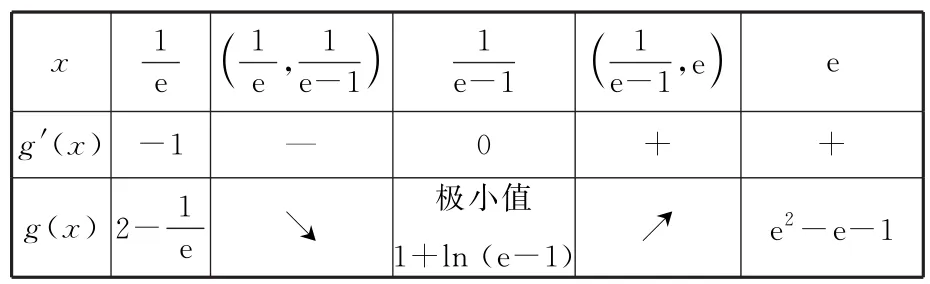
表1

由表知g(x)min=1+ln (e-1)。

故m∈（1+ln(e-1)，+∞）。