賞析熱點(diǎn)題 直擊定積分

■江蘇省沭陽高級中學(xué) 項敬磊

定積分是微積分學(xué)中的基本概念之一，學(xué)習(xí)時應(yīng)了解定積分的實(shí)際背景和基本思想，了解微積分基本定理的基本含義。近幾年高考加強(qiáng)了對此方面題型的考查，下面以幾道典型試題為例進(jìn)行剖析，以幫助同學(xué)們提升解決定積分問題的能力。

題型一 定積分的直接計算

例1計算的值。

解析：因為(ex+x2)'=ex+2x，所以

例2計算dx的值。

解 析：dx表示由y=，x=0，x=1及x軸所圍成的幾何圖形的面積。

點(diǎn)評：如果當(dāng)被積函數(shù)的原函數(shù)不好找，那么可以根據(jù)定積分的幾何意義，畫出函數(shù)的圖像，再求其面積。

題型二 利用定積分求平面圖形面積

例3曲線y=與直線y=x-1及x=4所圍成的封閉圖形的面積為( )。

A.2ln2 B.2-ln2

C.4-ln2 D.4-2ln2

解析：如圖1所示，y=和y=x-1的交點(diǎn)為(2，1)。由定積分的知識可知，封閉圖形的面積為:

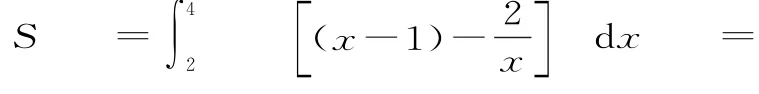
點(diǎn)評：利用定積分求平面圖形面積的一般步驟：(1)根據(jù)題意畫出圖形，并將圖形分割成若干曲邊梯形；(2)對每個曲邊梯形確定其存在的范圍，從而確定積分上限、下限；(3)確定被積函數(shù)，寫出相應(yīng)的定積分表達(dá)式；(4)求出各曲邊梯形的面積和，即各積分的絕對值之和。

幾種典型的曲邊梯形面積的計算方法:

(1)由三條直線x=a、x=b(a＜b)、x軸，和一條曲線y=f(x)(f(x)≥0)圍成的曲邊梯形的面積:

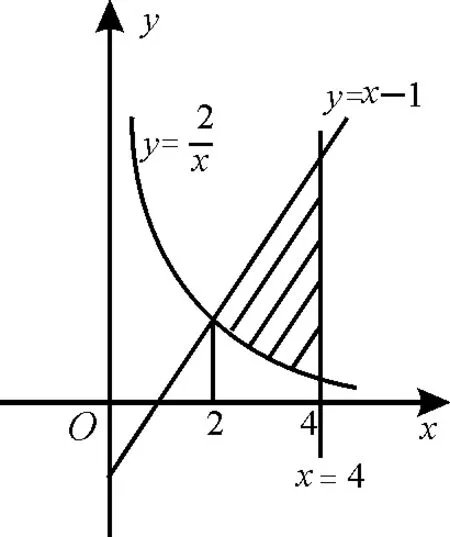
圖1

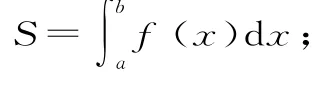
(2)由三條直線x=a、x=b(a＜b)、x軸，和一條曲線y=f(x)(f(x)≤0)圍成的曲邊梯形的面積:

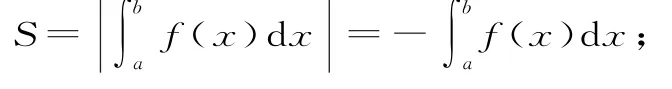
(3)由兩條直線x=a、x=b(a＜b)，兩條曲線y=f(x)、y=g(x)(f(x)≥g(x))圍成的平面圖形的面積:

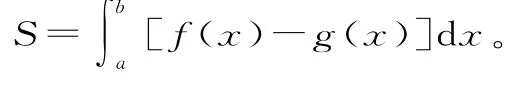
題型三 定積分在物理中的應(yīng)用

1.變速直線運(yùn)動的路程

例4一輛汽車在高速公路上行駛，由于遇到緊急情況而剎車，以速度v(t)=7-3t的單位:s，v的單位:m/s)行駛至停止，在此期間汽車?yán)^續(xù)行駛的距離(單位:m)是( )。……